C语言二叉树

时间:2022-06-28 配的上了吗人气:0

单值二叉树

难度简单

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回true；否则返回false。

示例 1：

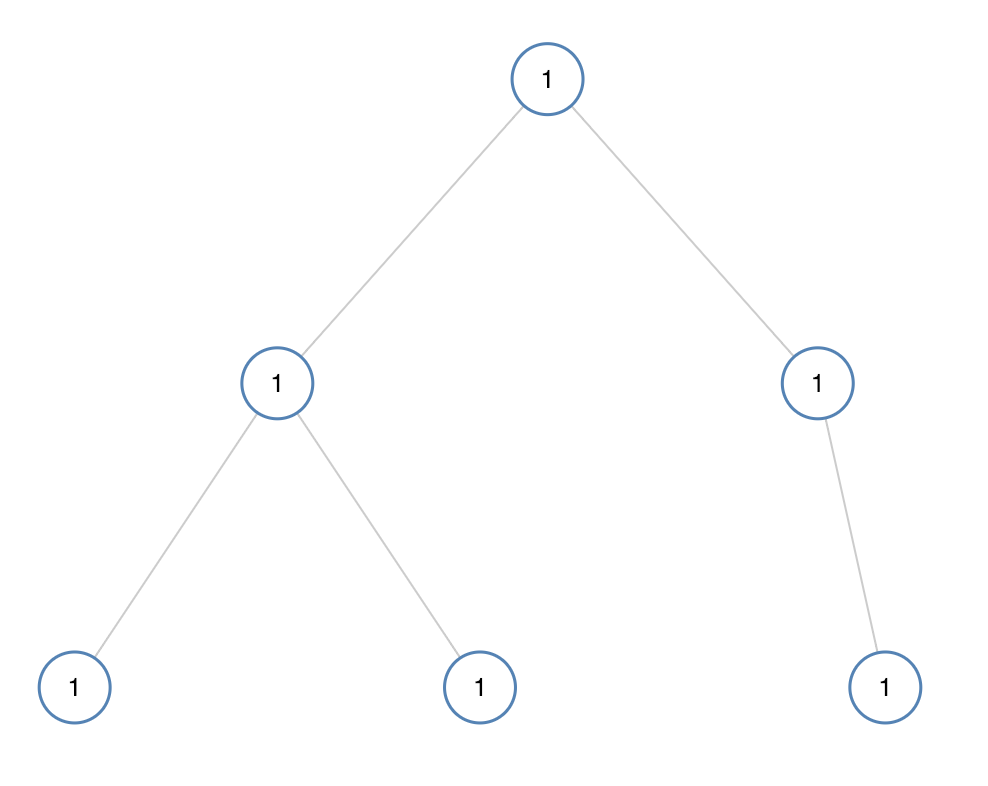
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

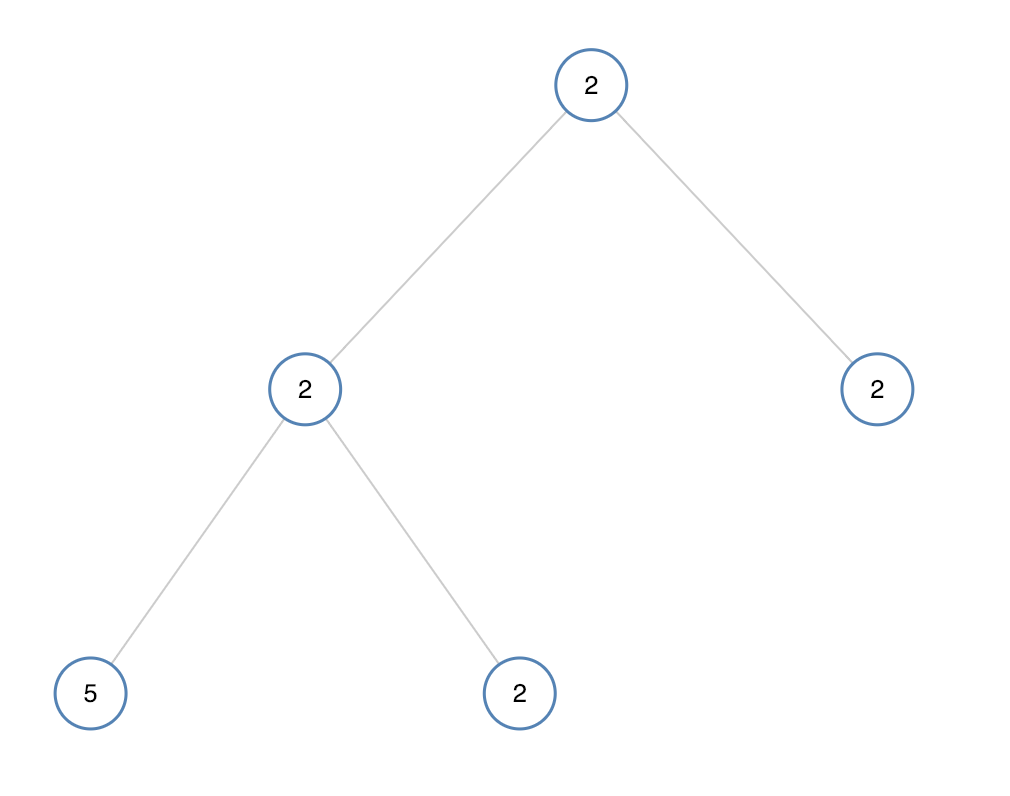
输入：[2,2,2,5,2]
输出：false

提示：

给定树的节点数范围是[1, 100]。

每个节点的值都是整数，范围为[0, 99]。

解1：

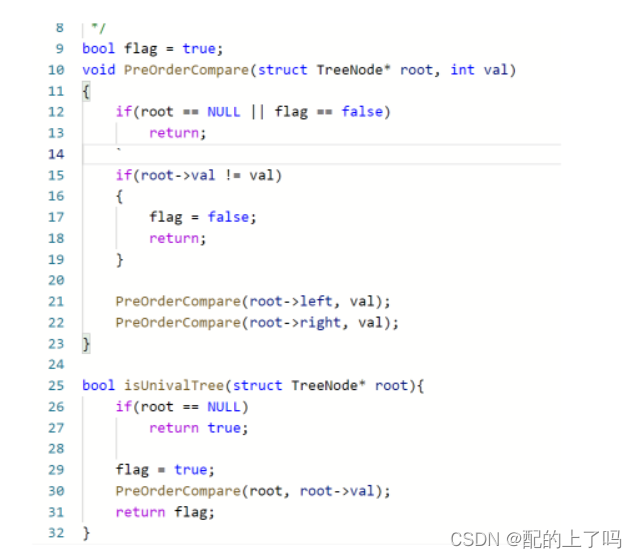
最简单易懂的解法，先序遍历一遍，把每个节点都和那个根节点的val值相比。最后判断flag是否为真，若为假，则表明树中有某节点的值不符。

其中的return语句是为了避免一些无意义的比较，但是其实第一个if的flag判断完全可以写在左递归之后，判断一下，如果左递归将flag置为了假，则直接return，不会进入右子树。如果按照上方解法来说，就是进入右子树之后，发现flag为假，再退出。

OJ题里的全局变量需要小心使用，若isUnivalTree里的flag不置为真，则多个测试用例时，可能会承接上一个测试用例假的结果。发生错误。

解法2：

class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        if(root == NULL)
            return true;
        if(root->left != nullptr && root->left->val != root->val)
            return false;
        if(root->right != nullptr && root->right->val != root->val)
            return false;
        return isUnivalTree(root->left) 
            && isUnivalTree(root->right);
    }
};

判断每个结点和其两个子节点是否相同，当然，需要确保子节点非空，若存在不同的，直接返回false，然后递归其左右子树。

其实这个的实质就是前序遍历，对每个结点的操作就是比较它和两个子节点的值是否相同。每个结点如果都和其左右子结点相同，那么这棵树也就都相同了，如果某处不同，则返回false，层层返回，最终也会返回flase。

解法3：

class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        bool ret = PreOrder(root, root->val);
        return ret;
    }
    bool PreOrder(TreeNode* root, int val)
    {
        if(root == nullptr)
            return true;
        if(root->val != val)
            return false;
        return PreOrder(root->left, val)
            && PreOrder(root->right, val);
    }
};

与2相比没什么大的改进，只是比较的方式不同而已，仍然是前序遍历的思想。第三个return里的&&挺好，左是假则不会对右求值。

相同的树

难度简单844

给你两棵二叉树的根节点p和q，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

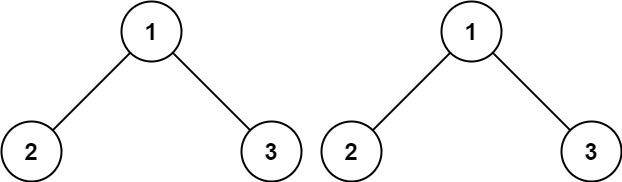
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

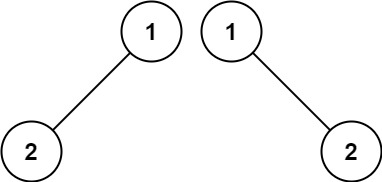
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

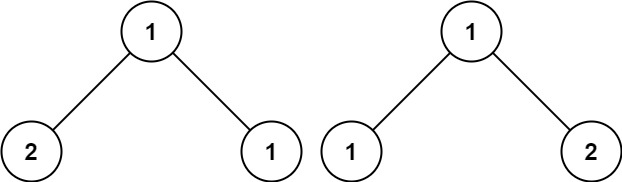
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围[0, 100]内
-104<= Node.val <= 104

通过次数344,943提交次数577,105

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr)
            return true;
        if(!(p!=nullptr && q!=nullptr && p->val == q->val))
            return false;
        bool retl = isSameTree(p->left,q->left);
        if(retl == false)
            return false;
        bool retr = isSameTree(p->right,q->right);
        if(retr == false)
            return false;
        return true;
/*
        return isSameTree(p->left,q->left)
            && isSameTree(p->right,q->right);
*/
    }
};

亿亿亿亿亿亿亿亿亿亿旧是前序遍历,只是两棵树同时遍历而已，判断是否相同，两个递归和最后那个注释的是效果相同的。

对称二叉树

难度简单1942

给你一个二叉树的根节点root，检查它是否轴对称。

示例 1：

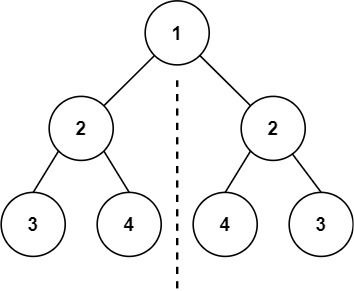
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

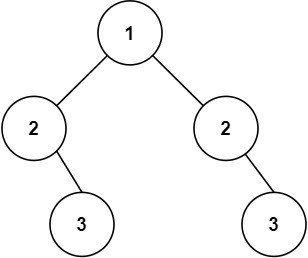
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围[1, 1000]内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

通过次数603,527提交次数1,044,923

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return isSame(root->left, root->right);
    }
    bool isSame(TreeNode* root1, TreeNode* root2)
    {
        if(root1 == nullptr && root2 == nullptr)  // 都是空，结束递归，且符合条件
            return true;
        // 两者根节点不相等，结束，不需要进一步判断了。
        if(!(root1 != nullptr && root2 != nullptr && root1->val == root2->val))  
            return false;
        // 进一步判断
        return isSame(root1->left,root2->right) && isSame(root1->right,root2->left);
    }
};

依旧是前序遍历。。。。。。。。。

另一棵树的子树

难度简单739

给你两棵二叉树root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在，返回true；否则，返回false。

二叉树tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。

示例 1：

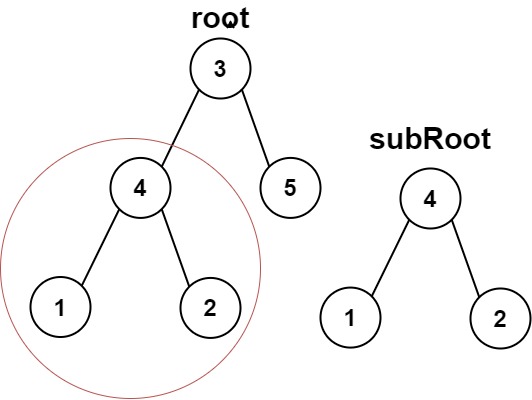
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

root树上的节点数量范围是[1, 2000]
subRoot树上的节点数量范围是[1, 1000]
-104<= root.val <= 104
-104<= subRoot.val <= 104

通过次数125,811提交次数264,360

class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == nullptr)
            return false;
        if(isSameTree(root, subRoot);)
            return true;
        if(isSubtree(root->left,subRoot);)
            return true;
        if(isSubtree(root->right,subRoot);)
            return true;
        return false;
    }
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr)
            return true;
        if(!(p!=nullptr && q!=nullptr && p->val == q->val))
            return false;
        bool retl = isSameTree(p->left,q->left);
        if(retl == false)
            return false;
        bool retr = isSameTree(p->right,q->right);
        if(retr == false)
            return false;
        return true;
    }
};

判断一个树是不是另一个的子树，这里的解法仍然是前序遍历，思路就是遍历每一个非空结点，把这个结点看成某一个树的根节点，只是这些根节点或大或小而已，然后调用isSameTree函数判断两个树是否相同。思路还是那么一个思路，没什么两样。

给出个错误解法吧：

class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == nullptr)
            return false;
        bool ret = isSameTree(root, subRoot);
        if(ret == true)
            return true;
        ret = isSameTree(root->left,subRoot);
        if(ret == true)
            return true;
        ret = isSameTree(root->right,subRoot);
        if(ret == true)
            return true;
        return false;
    }
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr)
            return true;
        if(!(p!=nullptr && q!=nullptr && p->val == q->val))
            return false;
        bool retl = isSameTree(p->left,q->left);
        if(retl == false)
            return false;
        bool retr = isSameTree(p->right,q->right);
        if(retr == false)
            return false;
        return true;
    }
};

这是起初写的错误解法，仔细想想还是容易理解的，34，不同，IsSameTree函数第二个if直接返回false，不会递归，然后进入3函数的左子树调用，仍然直接返回false，再走到3的右子树，也是直接返回false。并没有起到递归的作用。

小总结：

简单来说就是遍历了一遍，你可以直接把这个对结点的操作忽略掉，然后只看左递归和右递归，你就会发现，这两个函数恰好遍历了一遍整个树，然后你可以在适当的位置写一些操作，就是对每个结点的操作，比如572这个题，就是比较两个树是否相等。

#include<iostream>
#include<assert.h>
#include<string>
using namespace std;
typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = new BTNode();
	assert(newnode);
	newnode->data = x;
	newnode->right = nullptr;
	newnode->left = nullptr;
	return newnode;
}
BTNode* CreateTree(string s, int* pi)
{
    if(s[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    BTNode* root = BuyNode(s[(*pi)++]);
    root->left = CreateTree(s, pi);
    root->right = CreateTree(s, pi);
    return root;
}
void InOrder(BTNode* root)
{
    if(root == NULL)
        return;
    InOrder(root->left);
    cout<<root->data<<" ";
    InOrder(root->right);
}
int main()
{
    string s;
    cin >> s;
    int i = 0;
    BTNode* root = CreateTree(s, &i);
    InOrder(root);
    return 0;
}

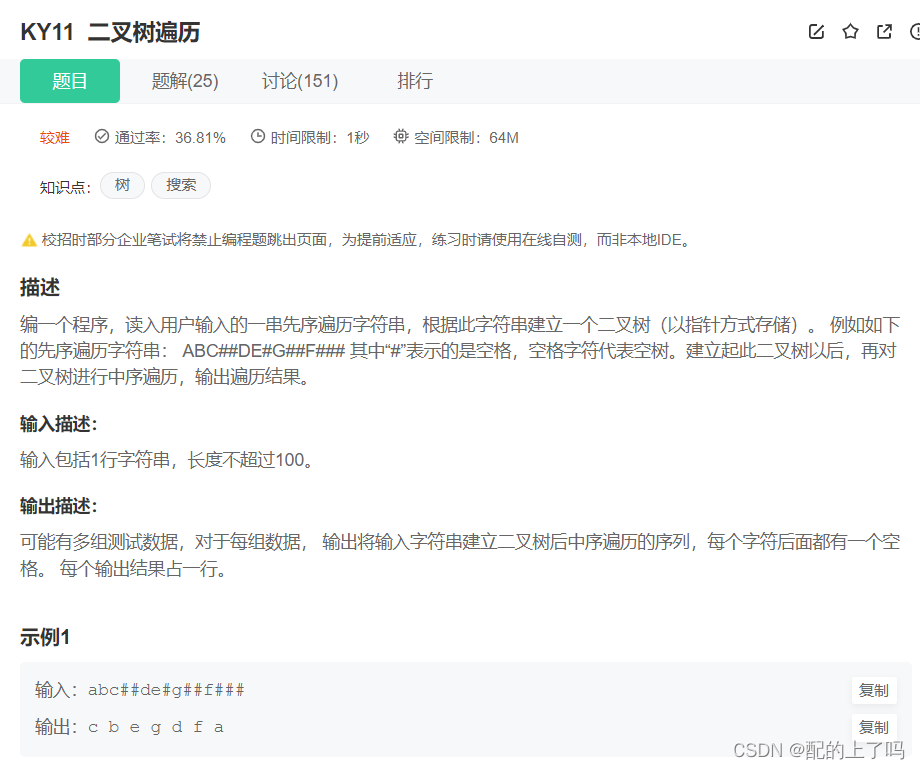
这个题相对而言就有点新颖了，创建正确的树是关键。后面的中序遍历就是一些基本操作了。

有关根据给定字符串创建合适的二叉树：其实根本上还是一种前序遍历的思路，可以直接把这个字符串看作一个正确的二叉树，s和pi的结合可以逐个遍历每个字符，每次进入函数都会创建对应的结点。而遇到#则返回空结点，作为上一个结点的左子树或者右子树，并同时结束递归。。。。。

销毁二叉树

void DestroyTree(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	// 后序销毁，先销毁左子树，再销毁右子树，最后销毁根节点，对于每一棵树都是这样的操作。
	DestroyTree(root->left);
	DestroyTree(root->right);
	delete root;
}

后序销毁。。

层序遍历

// 层序遍历 利用队列
void LevelOrder(BTNode* root)
{
	queue<BTNode*> q;
	if (root != NULL)
	{
		q.push(root);
	}
	while (!q.empty())
	{
		BTNode* root = q.front();
		cout << root->data << " ";
		q.pop();
		if (root->left)
		{
			q.push(root->left);
		}
		if (root->right)
		{
			q.push(root->right);
		}
	}
	cout << endl;
}

利用队列，先将根节点插入队列，然后出根节点，进根节点的两个子节点，当然也有可能是一个个，也有可能只有一个根节点。每次都是出一个结点，进这个结点的子节点。达到层序遍历的目的。

利用层序遍历判断一颗二叉树是否是完全二叉树

bool BinaryTreeComplete(BTNode* root)
{
	queue<BTNode*> q;
	if (root != NULL)
	{
		q.push(root);
	}
	while (!q.empty())
	{
		BTNode* root = q.front();
		q.pop();
		if (root)
		{
			q.push(root->left);
			q.push(root->right);
		}
		else
		{
			break;
		}
	}
	while (!q.empty())
	{
		if (q.front() != NULL)
			return false;
		q.pop();
	}
	return true;
}

完全二叉树的特点：层序遍历后，前方遍历的一定全是非空结点，后方一定全是空结点，利用这一特点进行判断。即：遇到空结点之后再判断队列中是否后续都是空结点。

加载全部内容