Matlab嗅觉优化算法
电力系统与算法之美 人气:01.概述
嗅觉剂优化是一种新颖的优化算法，旨在模仿气味分子源尾随的药剂的智能行为。该概念分为三个阶段（嗅探，尾随和随机）是独特且易于实现的。此上传包含 SAO 在 37 个 CEC 基准测试函数上的实现。
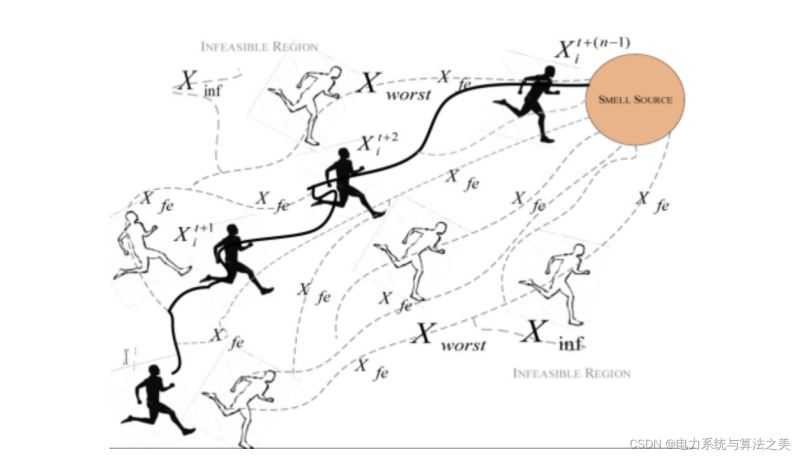
2.37 个 CEC 基准测试函数代码
function [lb,ub,dim,fobj] = Select_Function(F)
switch F
case 'F1'
%Admijan
fobj = @F1;
lb=[-1 -1];
ub=[2 1];
dim=2;
case 'F2'
%Beale
fobj = @F2;
dim=2;
lb=-4.5*ones(1,dim);
ub=4.5*ones(1,dim);
case 'F3'
%Bird
fobj = @F3;
dim=2;
lb=-2*pi*ones(1,dim);
ub=2*pi*ones(1,dim);
case 'F4'
%Bohachevsky
fobj = @F4;
dim=2;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F5'
% Booth
fobj = @F5;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F6'
%Branin RCOS1
fobj = @F6;
lb=[-5,0];
ub=[10, 15];
dim=2;
case 'F7'
%Branin RCOS2
fobj = @F7;
dim=2;
lb=-5*ones(1,dim);
ub=15*ones(1,dim);
case 'F8'
%Brent
fobj = @F8;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F9'
%Bukin F2
fobj = @F9;
dim=2;
lb=[-15 -3];
ub=[-5 3];
case 'F10'
%six-hump
fobj = @F10;
dim=2;
lb=-5*ones(1,dim);
ub=5*ones(1,dim);
case 'F11'
%Chichinadze
fobj = @F11;
dim=2;
lb=-30*ones(1,dim);
ub=30*ones(1,dim);
case 'F12'
%Deckkers-Aarts
fobj = @F12;
dim =2;
lb=-20*ones(1,dim);
ub=20*ones(1,dim);
case 'F13'
%Easom
dim=2;
fobj=@F13;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F14'
%Matyas
fobj = @F14;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F15'
%McComick
fobj = @F15;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F16'
%Michalewicz2
fobj = @F16;
dim=2;
lb=0*ones(1,dim);
ub=pi*ones(1,dim);
case 'F17'
%Quadratic
fobj = @F17;
dim=2;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F18'
%Schaffer
dim=2;
fobj = @F18;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F19'
%StyblinskiTang
fobj = @F19;
dim=2;
lb=-5*ones(1,dim);
ub=5*ones(1,dim);
case 'F20'
%Box-Betts
fobj = @F20;
dim=3;
lb=[0.9 9 0.9];
ub=[1.2 11.2 1.2];
case 'F21'
%Colville
fobj = @F21;
dim=4;
lb=-1*ones(1,dim);
ub=1*ones(1,dim);
case 'F22'
%Csendes
fobj = @F22;
dim=4;
lb=-1*ones(1,dim);
ub=1*ones(1,dim);
case 'F23'
% Michalewicz 5
fobj = @F23;
dim=5;
lb=0*ones(1,dim);
ub=pi*ones(1,dim);
case 'F24'
%Miele Cantrell
dim=4;
fobj = @F24;
lb=-1*ones(1,dim);
ub=1*ones(1,dim);
case 'F25'
% Step
fobj = @F25;
dim=5;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F26'
%Michalewicz
fobj = @F26;
dim=10;
lb=0*ones(1,dim);
ub=pi*ones(1,dim);
case 'F27'
%Shubert
fobj = @F27;
dim=5;
lb=-10*ones(1,dim);
ub=10*ones(1,dim);
case 'F28'
%Ackley
dim=30;
fobj = @F28;
lb=-32*ones(1,dim);
ub=32*ones(1,dim);
case 'F29'
%Brown
fobj = @F29;
dim=30;
lb=-1*ones(1,dim);
ub=4*ones(1,dim);
case 'F30'
%Ellipsoid
dim=2;
fobj = @F30;
lb=-5.12*ones(1,dim);
ub=5.12*ones(1,dim);
case 'F31'
% Grienwank
fobj = @F31;
dim=30;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F32'
%Mishra
fobj = @F32;
dim=30;
lb=0*ones(1,dim);
ub=1*ones(1,dim);
case 'F33'
%Quartic
dim=30;
fobj = @F33;
lb=-1.28*ones(1,dim);
ub=1.28*ones(1,dim);
case 'F34'
%Rastrigin
fobj = @F34;
dim=30;
lb=-5.12*ones(1,dim);
ub=5.12*ones(1,dim);
case 'F35'
%Rosenbrock
fobj = @F35;
dim=30;
lb=-30*ones(1,dim);
ub=30*ones(1,dim);
case 'F36'
% Salomon
fobj = @F36;
dim=30;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
case 'F37'
%Sphere
fobj = @F37;
dim=30;
lb=-100*ones(1,dim);
ub=100*ones(1,dim);
end
end
function o=F1(x)
% Adjiman
o=(cos(x(:,1)).*sin(x(:,2))-x(:,1)./(x(:,2).^2+1));
end
function o=F2(x)
% Beale
o=(1.5-x(:,1)+(x(:,1).*(x(:,2)))).^2+(2.25-x(:,1)+(x(:,1).*(x(:,2)).^2)).^2+...
(2.625-x(:,1)+(x(:,1).*(x(:,2)).^3)).^2;
end
function o=F3(x)
% Bird
o=sin(x(:,2)).*(exp(1-cos(x(:,1))).^2)+cos(x(:,1)).*(exp(1-sin(x(:,2))).^2)...
+(x(:,1)+(x(:,2))).^2;
end
function o=F4(x)
% Bohachevsky
W=0;
[a,dim]=size(x);
for i=1:dim-1
W=W+x(:,i).^2+2.*x(:,i+1).^2-0.3.*cos(3.*pi.*x(:,i+1))-0.4.*cos(4.*pi.*(x(:,i+1)))+0.7;
end
o=W;
end
function o=F5(x)
%Booth
o=(x(:,2)-(5.1*x(:,1).^2/(4*pi*2))+(5*x(:,1)/pi)-6).^2+...
10*(1-1/(8*pi)).*cos(x(:,1))+10;
end
function o=F6(x)
% Branin RCOS 1
o=(x(:,2)-(5.1*x(:,1).^2/(4*pi*2))+(5*x(:,1)/pi)-6).^2+...
10*(1-1/(8*pi)).*cos(x(:,1))+10;
end
function o=F7(x)
% Branin RCOS 2
a=1; b=5.1/(4*pi^2); c=5/pi; d=6; e=10; g=1/(8*pi);
f1=a*(x(:,2)-b*x(:,1).^2+c*x(:,1)-d).^2;
f2=e*(1-g)*cos(x(:,1)).*cos(x(:,2));
f3=log(x(:,1).^2+x(:,2)+1);
o=-1/(f1+f2+f3+e);
end
function o=F8(x)
%Brent
o=(x(:,1)+10).^2+(x(:,1)+10).^2+exp(-x(:,1).^2-x(:,2).^2);
end
function o=F9(x)
%Bukin F2
o=(abs(x(:,1)-0.01.*x(:,2).^2))+0.01.*abs(x(:,2)+10);
end
function o=F10(x)
%Camel Six Hump
o=(4-2.1*x(:,1).^2+(x(:,1).^4)/3).*x(:,1).^2+x(:,1).*x(:,2)+...
(4*x(:,2).^2-4).*x(:,2).^2;
end
function o=F11(x)
%Chichinadze
o=x(:,1).^2-12*x(:,1)+11+10*cos(pi*x(:,1)/2)+8*sin(5*pi*x(:,1)/2)-...
((1/5)^0.5)*exp(-0.5*(x(:,2)-0.5).^2);
end
function o=F12(x)
% Deckkers-Aarts
o=10^5*x(:,1).^2+x(:,2).^2-(x(:,1).^2+x(:,2).^2).^2+...
10^(-5)*(x(:,1).^2+x(:,2).^2).^4;
end
function o = F13(x)
% Easom
o=-cos(x(:,1)).*cos(x(:,2)).*exp(-(x(:,1)-pi).^2-(x(:,2)-pi).^2);
end
function o=F14(x)
% Evaluate Matyas
o=0.26*(x(:,1).^2+x(:,2).^2)-0.48*x(:,1).*x(:,2);
end
function o=F15(x)
% McCormick
o=mccormick(x);%
end
function o=F16(x)
% Michalewicz2
[~,d]=size(x);
W=0;
for i=1:d
W=sin(x(:,1)).*sin(i*x(:,i).^2/pi).^2*d;
end
o=-W;
end
function o=F17(x)
% Quadratic
o=-3803.84-138.08*x(:,1)-232.92*x(:,2)+128.08*x(:,1).^2+203.64*x(:,2).^2+182.25*x(:,1).*x(:,2);
end
function o=F18(x)
% Evaluate Schaffer
[~,d]=size(x);
w=0;
for i=1:d-1
w=w+((x(i).^2+x(i+1).^2).^.5).*(sin(50.*(x(i).^2+x(i+1).^2).^0.1)).^2;
end
o=w;
end
function o=F19(x)
% Styblinki's Tang
[~,d]=size(x);
W=0;
for i=1:d
W=W+(x(:,i).^4-16.*x(:,i).^2+5.*x(:,i));
end
o=W.*0.5;
end
function o=F20(x)
% Box-Betts
[~,d]=size(x);
W=0;
for i=1:d
g=exp(-0.1.*(i+1)).*x(:,1)-exp(-0.1.*(i+1)).*x(:,2)-((exp(-0.1.*(i+1)))-exp(-(i+1)).*x(:,3));
W=W+g.^2;
end
o=W;
end
function o=F21(x)
% Colville
o=100*(x(:,1)-x(:,2).^2).^2+(1-x(:,1)).^2+90*(x(:,4)-x(:,3).^2).^2+...
(1-x(:,3)).^2+10.1*((x(:,2)-1).^2+(x(:,4)-1).^2)+...
19.8*(x(:,2)-1).*(x(:,4)-1);
end
function o=F22(x)
% Csendes
[~,d]=size(x);
aa=0;
for i=1:d
aa=aa+x(:,i).^6.*(2+sin(1/x(:,i)));
end
o=aa;
end
function o=F23(x)
% Michalewicz 5
[~,d]=size(x);
W=0;
for i=1:d
W=sin(x(:,1)).*sin(i*x(:,i).^2/pi).^2*d;
end
o=-W;
end
function o=F24(x)
%Miele Cantrell
o=(exp(-x(:,1))-x(:,2)).^4+100*(x(:,2)-x(:,3)).^6+...
(tan(x(:,3)-x(:,4))).^4+x(:,1).^8;
end
function o=F25(x)
% Evaluate Step
[~,d]=size(x);
W=0;
for i=1:d
W=W+(floor(x(:,i)+0.5)).^2;
end
o=W;
end
function o=F26(x)
% Evaluate Michalewicz 10
[~,d]=size(x);
W=0;
for i=1:d
W=sin(x(:,1)).*sin(i*x(:,i).^2/pi).^2*d;
end
o=-W;
end
function o=F27(x)
% shubert
[~,d]=size(x);
s1=0;
s2=0;
for i = 1:d
s1 = s1+i*cos((i+1)*x(1)+i);
s2 = s2+i*cos((i+1)*x(2)+i);
end
o = s1*s2;
end
% F28--Ackley
function o = F28(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
function o=F29(x)
[~,d]=size(x);
% Brown
a=0;
for i=1:d-1
a=(x(:,i).^2).^(x(:,i+1)+1)+(x(:,i+1).^2).^(x(:,i).^2+1);
end
o=a;
end
function o=F30(x)
% Ellipsoid
[~,d]=size(x);
W=0;
for i=1:d
W=W+i.*x(:,1).^2;
end
o=W;
end
%Grienwank
function o=F31(x)
o=griewank(x);
end
function o=F32(x)
% Mishra
[~,d]=size(x);
a=0;
for i=1:d-1
a=a+x(:,i);
end
aa=d-a;
b=0;
for j=1:d-1
b=b+x(:,j);
end
W=abs((1+d-b).^aa);
o=W;
end
% --Quartic
function o = F33(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
%Rastrigin
function o=F34(x)
o=rastrigin(x);
end
% Rosenbrock
function o = F35(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
function o=F36(x)
% salomon
x2 = x.^2;
sumx2 = sum(x2, 2);
sqrtsx2 = sqrt(sumx2);
o = 1 - cos(2 .* pi .* sqrtsx2) + (0.1 * sqrtsx2);
end
function o = F37(x)
%Sphere
o=sum(x.^2);
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end3.F1 Matlab代码仿真
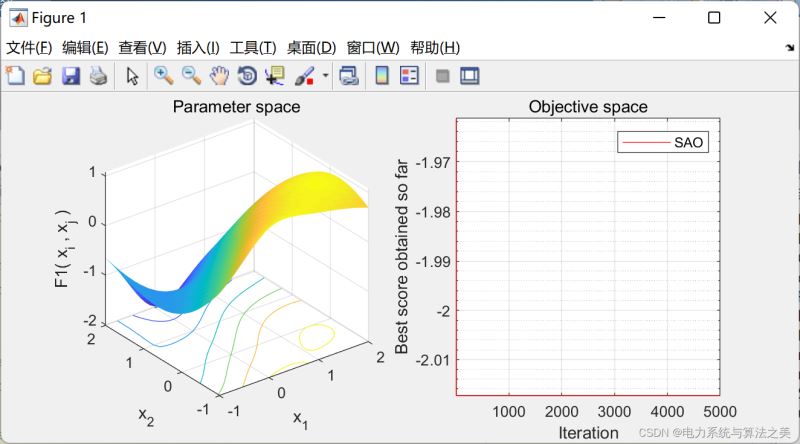
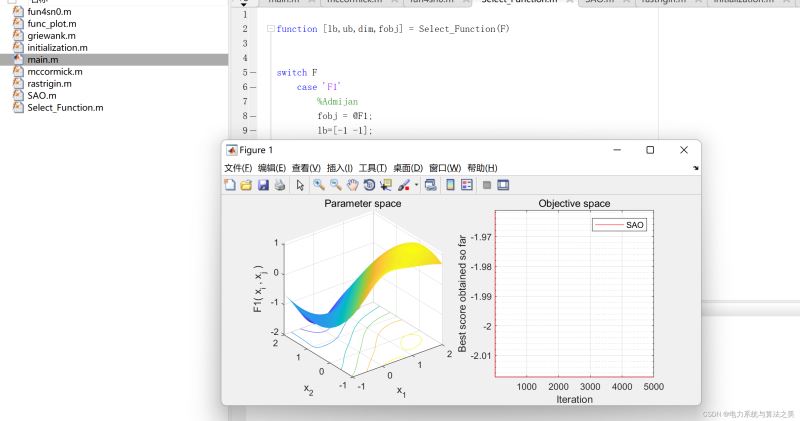
加载全部内容