Matlab灰色预测

时间:2022-06-02 slandarer 人气:0

模型介绍

略微带过一下原理：

灰色预测对于趋势不强的数据，将其原始数据进行累加后得到具有明显趋势的新数据进行拟合，假设原数据为：

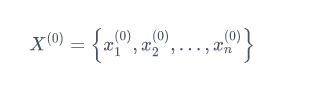
则新数据集X⁽¹⁾中数据为：

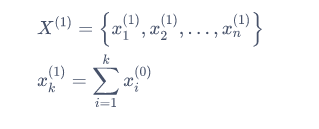
通常认为累加数据服从指数分布，欸那我们直接假设：

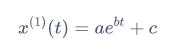
直接进行一个非线性拟合不就完事了，但是，从小学二年级开始，老师就教导我们，像这用指数函数拟合啊，各个参数的变化对于整体曲线的影响效果差别很大啊，直接拟合误差会很大啊，怎么能给他整成一个线性拟合啊？(直接拟合我有试过，能够大体描述趋势并做出预测，但是误差会比灰色预测大一点)。

指数函数一般符合一个微分方程：

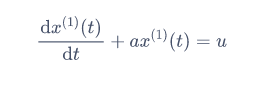
解常微分方程易得：

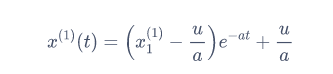
这样我们只需要将a,u这俩常数求出来就能得到x⁽¹⁾(t) ,就能得到X⁽¹⁾序列然后逐项做差就能得到X⁽⁰⁾序列。

当k≤t≤k+1时，有：

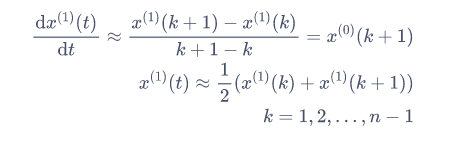
带入回之前的微分方程就有：

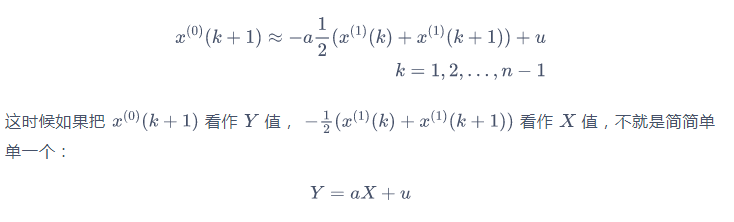
实际上直接进行线性拟合就好了，当然我们也可以拿最小二乘法装模作样的分析一下,令:

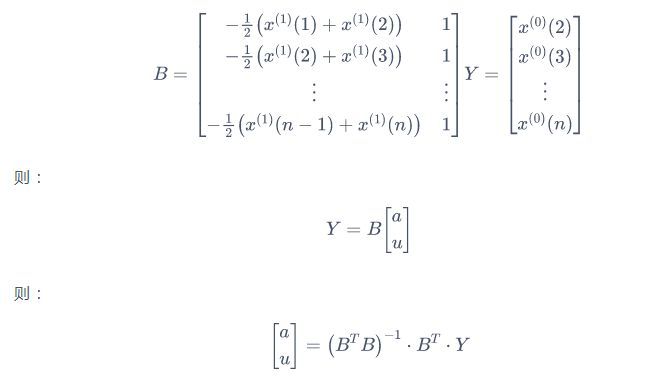
基础代码

核心代码非常短，只有六行，代码中给出了详细的注释，基础绘图还是MATLAB风比较简陋，后面会给出图像修饰代码。

X0=[15 16.1 17.3 18.4 18.7 19.1 19.9 21.3 22.5];
t=1:9;    % 原始数据自变量范围
pt=10:12; % 预测数据自变量范围

X1=cumsum(X0);                    % 累加生成趋势明显新序列
Z=X1(1:end-1)+diff(X1)./2;        % 均值，即(X1(1:end-1)+X1(2:end))./2
a_u=polyfit(-Z,X0(2:end),1);      % a_u=(B'*B)\B'*Y,B=[-Z,ones]
a=a_u(1);u=a_u(2);
P=(X1(1)-u/a)./exp(a.*([t,pt]-1))+u/a; % 求X1拟合值
P=[P(1),diff(P)];                      % X1逐项做差求预测值

% 绘图
plot([t,pt],P,'*-');
hold on
plot(t,X0,'s-')  
legend('预测值','真实值');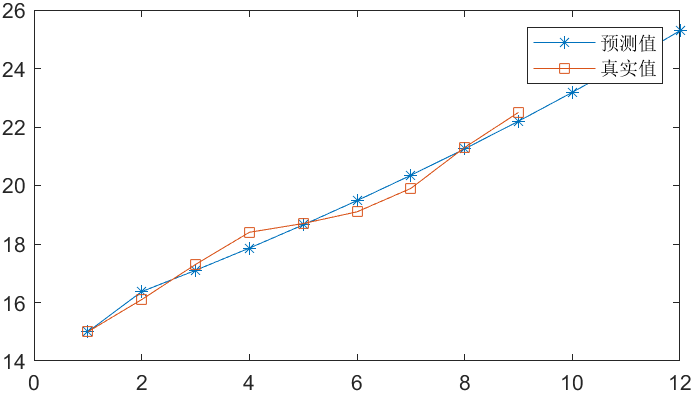

基础代码+修饰

X0=[15 16.1 17.3 18.4 18.7 19.1 19.9 21.3 22.5];
t=1:9;    % 原始数据自变量范围
pt=10:12; % 预测数据自变量范围

X1=cumsum(X0);                    % 累加生成趋势明显新序列
Z=X1(1:end-1)+diff(X1)./2;        % 均值，即(X1(1:end-1)+X1(2:end))./2
a_u=polyfit(-Z,X0(2:end),1);      % a_u=(B'*B)\B'*Y,B=[-Z,ones]
a=a_u(1);u=a_u(2);
P=(X1(1)-u/a)./exp(a.*([t,pt]-1))+u/a; % 求X1拟合值
P=[P(1),diff(P)];                      % X1逐项做差求预测值

% 绘图
plot([t,pt],P,'s-','Color',[82,124,179]./255,'MarkerFaceColor',[82,124,179]./255,...
    'MarkerEdgeColor',[1,1,1],'LineWidth',2,'MarkerSize',16)  
hold on
plot(t,X0,'d-.','Color',[169,64,71]./255,'MarkerFaceColor',[169,64,71]./255,...
    'MarkerEdgeColor',[1,1,1],'LineWidth',2,'MarkerSize',16)  

% 增添图例
lgd=legend('fitting result','original data');
lgd.Location='best';
lgd.FontSize=16;

% 坐标区域修饰
ax=gca;grid on;box off
ax.LineWidth=2;
ax.Color=[249,250,245]./255;
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.GridLineStyle='-.';
ax.XColor=[1,1,1].*.2;
ax.YColor=[1,1,1].*.2;
ax.FontName='Cambria';
ax.FontSize=14;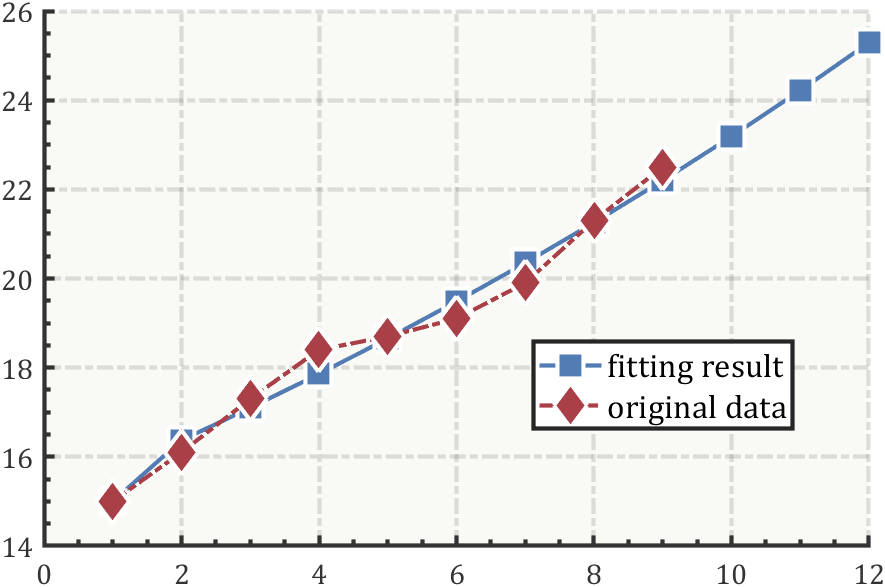

加载全部内容