浮点数乘法和整形乘除法效率
concyclics 人气:0前言
最近在做一个比赛,包含了如下内容:
环上边的转账金额需要为前一条边的转账金额的90%-110%(含边界)。
对于“金额”的处理,我一开始以浮点数乘法(乘1.1和0.9)外加eps修正精度的方式进行判断,有一位朋友看完我的代码后提出意见:
C*S: 如果确定只有两位小数且不炸范围,那么有办法完全消除浮点数的使用。

然后我照着整形的方式改,结果发现更慢了……
于是有了如下实验:
测试
1. 整形除法和浮点数乘法
我们每次把整形加减自身/10,来模拟上下浮动10%,并把浮点形乘1.1(0.9)并修正eps精度误差。
测试代码如下:
int main()
{
const int N=1e8;
int64_t t1=clk();
for(int i=0;i<N;i++)
{
long long x=i;
x=x+x/10;
x=x-x/10;
}
int64_t t2=clk();
for(int i=0;i<N;i++)
{
double x=i;
x=x*1.1+1e-5;
x=x*0.9-1e-5;
}
int64_t t3=clk();
cout<<"long long "<<t2-t1<<endl;
cout<<"double "<<t3-t2<<endl;
}
结果:
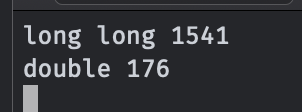
long long花了1541ms,是double的几乎十倍。
除法相较于加减乘有较大的常数。
2. 把整形预先乘10来比较
现在再试试另一种方法,即把0.9x<y<1.1x变成9x<10y<11x的形式,这样不就全是整形乘法了吗?但是三次整形乘法和两次浮点乘法两次浮点加减法哪个慢呢?
测试代码如下:
int main()
{
const int N=1e8;
int64_t t1=clk();
for(int i=0;i<N;i++)
{
long long x=i;
x=x*11;
x=x*9;
x=x*10;
}
int64_t t2=clk();
for(int i=0;i<N;i++)
{
double x=i;
x=x*1.1+1e-5;
x=x*0.9-1e-5;
}
int64_t t3=clk();
cout<<"long long "<<t2-t1<<endl;
cout<<"double "<<t3-t2<<endl;
}
结果:
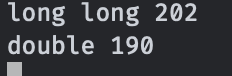
我们可以看到,虽然单次浮点乘法的常数会略大于整形乘法,但是三次整形乘法还是慢于两次浮点乘法的。
3. 单次浮点乘法和整形乘法比较
测试代码:
int main()
{
const int N=1e8;
int64_t t1=clk();
for(int i=0;i<N;i++)
{
long long x=i;
x=x*11ll;
}
int64_t t2=clk();
for(int i=0;i<N;i++)
{
double x=i;
x=x*1.1;
}
int64_t t3=clk();
cout<<"long long "<<t2-t1<<endl;
cout<<"double "<<t3-t2<<endl;
}
结果:
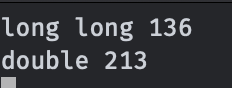
我们可以看到,单次浮点乘法的常数大概会比整形大50%左右,所以三次整形乘法还是略慢于两次浮点乘法的。
总结
这次实验给了我一个思路,即在对精度不敏感的情况下,可以把整形的/10之类的除法,换成*0.1的浮点乘法来提速,更多关于浮点数乘法和整形乘除法效率的资料请关注其它相关文章!
加载全部内容