C语言排序

时间:2022-06-02 Mi ronin 人气:0

一.选择排序

1.1 选择排序引入

就像炒股一样，有的人爱炒短线，不断的买进卖出通过差价来盈利，但是频繁的买进卖出，也会因为频繁的手续费和一系列费用获益较少；有的人，不断的进行观察和判断，等到时机一到，果断买进或卖出，这种人交易次数少，而最终收获颇丰；正如我们所说的第一种人就类似排序里的冒泡排序，而第二种人就在排序中可以理解为：在排序时找到合适的关键字再做交换，并且只交换一次完成相应关键字的排序；这就是我们要说的选择排序。

1.2 选择排序的基本思想与算法分析

基本思想：从头至尾扫描序列，找出最小的一个元素，和第一个元素交换，接着从剩下的元素中继续这种选择和交换方式，最终得到一个有序序列

算法分析：

第1步:在未排序的n个数(a [0] ~a [n- 1])中找到最小数，将它与a [0]交换;
第2步:在剩下未排序的n- 1个数(a [1] ~a [n- 1])中找到最小数，将它与a[1]交换;
第n-1步:在剩下未排序的2个数(a [n-2] ~a [n- 1] )中找到最小数，将它与a [n-2]交换；
得到一个排好序的序列。

1.3 实例说明

以12，32，2，60，42，98为例，排序过程如下：

数字底下有横线的为已排好序的
n个值排n-1次即可
每一次都找一个最小值放到前面

1.4 代码实现

代码如下：

void SelectSort(int arr[], int len)
{
	for (int i = 0; i < len - 1; i++)//趟数
	{
		int min_index = i;
		for (int j = i + 1; j < len; j++)//控制找最小值
		{
			if (arr[j] < arr[min_index])
			{
				min_index = j;
			}
		}
		//当内层for循环跑完，此时min_index保存是就是当前待排序序列中最小值的下标
		if (min_index != i)//如果找到的最小值下标  不等于 待排序序列的第一个值的下标  则才有交换的必要性
		{
			int tmp = arr[i];
			arr[i] = arr[min_index];
			arr[min_index] = tmp;
		}
	}
}

1.5 性能分析

时间复杂度：O（n^2）。
空间复杂度：O（1）。
稳定性：不稳定。

尽管与冒泡排序的时间复杂度同为O（n^2），但选择排序的性能还是略优于冒泡排序的。

二.基数排序

2.1 基数排序基本思想与算法步骤

基本思想：将整数按位数切割成不同的数字，然后按每个位数分别比较，最后合并结果。

算法步骤：

将所有待比较数值统一为同样的数位长度，数位较短的数前面补零；
从最低位开始，依次进行一次排序；
从最低位排序一直到最高位排序完成以后, 整合后数列就变成一个有序序列。

2.2 实例说明

以12，32，2，620，42，98，122，289，987，37，56，90为例，排序过程如下：

1.以个位数跑一趟：

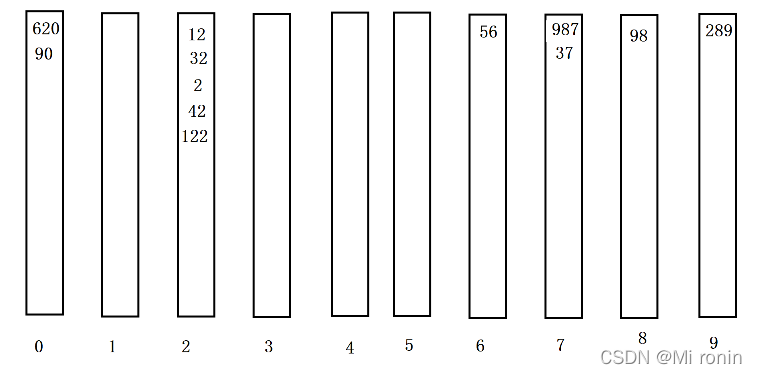
个位排序的最终结果：

620，90，12，32，2，42，122，56，987，27，98，289

（这些数据只看个位的话为有序）

2.以十位跑一趟：

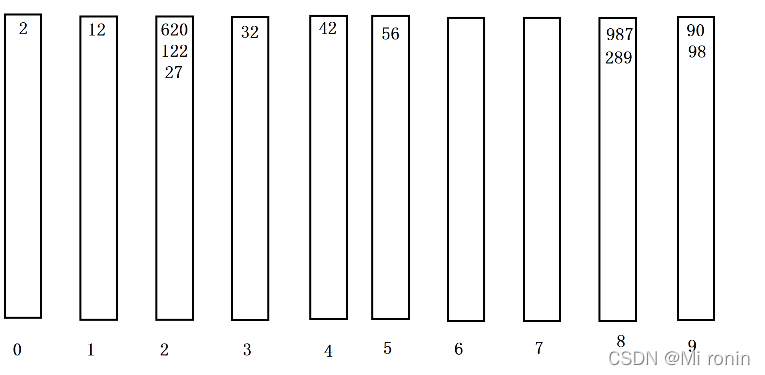
十位排序的最终结果：

2，12，620，122，27，32，43，56，987，289，90，98

（这些数据只看十位的话为有序）

3.以百位跑一趟：

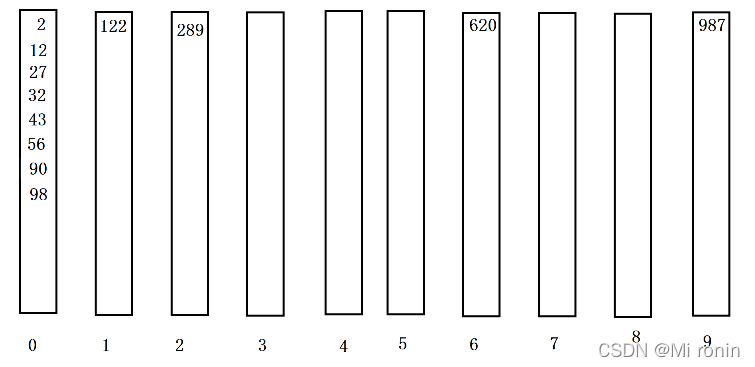
百位排序的最终结果：

2，12，27，32，43，56，90，98，122，289，620，987

（数据已完全有序）

2.3 代码实现

代码如下：

//获取数组中最大值的位数
int Get_figure(int* arr, int len)
{
	int max = 0;
	for (int i = 0; i < len; i++)
	{
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}
	int count = 0;
	while (max != 0)
	{
		count++;
		max /= 10;
	}
	return count;
}
//这个函数告诉我传进来的参数n的，对应fin位是多少
//1234,2 -> 2    345,1 ->4    0078,3 -> 0     56789,4 -> 5
int Get_Num(int n, int fin)
{
	for (int i = 0; i < fin; i++)//这里代表需要n 先丢几位最低位
	{
		//n = n/10;
		n /= 10;
	}
	return n % 10;//此时获取剩余属于的最低位即可
}
//一趟桶排序    fin代表这一趟是根据哪个位进行排序（个，十，百......）   0->个位  1->十位...
void Radix(int* arr, int len, int fin)//时间复杂度O(n)
{
	//先将10个桶申请好
	int bucket[10][100] = { 0 };
	int num[10] = { 0 };  //num[1] 代表1号桶中有多少个有效值
	//将所有数据从左向右向对应的桶中存放
	for (int i = 0; i < len; i++)
	{
		int index = Get_Num(arr[i], fin);
		bucket[index][num[index]] = arr[i];
		num[index]++;
	}
	//按照0->9号桶的顺序，依次遵循先进先出的规则将所有值取出来
	int k = 0;
	for (int i = 0; i <= 9; i++)//0->9号桶依次取
	{
		for (int j = 0; j < num[i]; j++)//对应的桶内，从上到下依次取值
		{
			arr[k++] = bucket[i][j];//取出来的值 从前向后放到arr中
		}
	}
}
//基数排序（桶排序）  时间复杂度(d*n)（假设最大值的位数是d） 空间复杂度O（d*n） 稳定性：稳定
void RadixSort(int* arr, int len)
{
	//assert
	//1.首先需要知道 数据中最大值有多少位
	int count = Get_figure(arr, len);

	for (int i = 0; i < count; i++) //D
	{
		Radix(arr, len, i);
	}
}

2.4 性能分析

假设最大值的位数是d

时间复杂度：O （d*n）。
空间复杂度：O （d*n）。
稳定性：稳定。

加载全部内容