C++贪心算法
Andy-wen 人气:0贪心1
实验题目:减肥的小K1
题目描述:
小K没事干,他要搬砖头,为了达到较好的减肥效果,教练规定的方式很特别:每一次,小K可以把两堆砖头合并到一起,消耗的体力等于两堆砖头的重量之和。经过 n-1次合并后, 就只剩下一堆了。小K在搬砖头时总共消耗的体力等于每次合并所耗体力之和。小K为了偷懒,希望耗费的体力最小。例如有 3堆砖头,数目依次为 1、2、9 。可以先将 1 、 2 堆合并,新堆数目为3 ,耗费体力为 3 。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12 ,耗费体力为12 。所以总共耗费体力 =3+12=15。可以证明 15为最小的体力耗费值。
输入要求:
共两行。
第一行是一个整数 n(1≤n≤1000) ,表示砖头堆数。
第二行n个整数,每个整数表示每堆砖头的砖头块数。
输出要求:
一个整数,也就是最小的体力耗费值。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, a[1000], sum = 0, i;
cin >> n;
for (i = 0; i < n; i++)
{
cin >> a[i];
}
sort(a, a + n);
for (i = 0; i < n - 1; i++) {
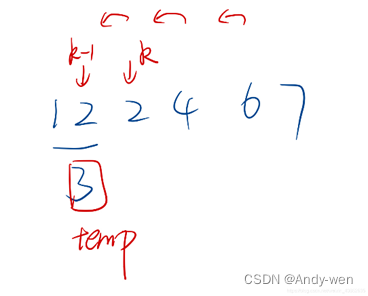
int temp = a[i + 1] + a[i];//记录前两个最小的值
int k = i + 2;//k为第三个的下标
while (a[k] < temp && k < n) {//比较第三个和前两个的和,若第三个比前两个要小
a[k - 1] = a[k];//前移
k++;
}
a[k - 1] = temp;
sum += temp;
}
cout << sum << endl;
return 0;
}
算法分析与知识点:
本题主要运用贪心的思想,每次都在全部砖头中找到重量最轻的两堆进行合并以达到最节约体力的目的。
因此要先对全部砖头按重量进行排序,需要注意的是再合并完两堆砖头后需要对后续砖头堆进行重新排序,第一次WA就是因为没有对后续砖头堆进行重新排序。
实验题目:最小跳数
题目描述:
给定一个非负整数数组,假定你的初始位置为数组第一个位置。数组中的每个元素代表你在那个位置能够跳跃的最大长度。你的目标是到达最后一个下标位置,并且使用最少的跳跃次数。
输入要求:
输入一组非负整数数组,数组长度不超过500。
输出要求:
最少经过几次跳跃,可以到达最后一个位置。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
int main() {
int n = 0, a[501];
while (cin >> a[n++]);
n = n - 1;
// maxPos 记录当前最远能到哪里
// step 记录当前进行了几跳
// end 记录了当前最远能到哪里的边界
int maxPos = 0, end = 0, step = 0;
for (int i = 0;i < n - 1;i++) {
if (maxPos >= i) { //判断能否继续探索
maxPos = max(maxPos, i + a[i]);
if (i == end) { // 到达边界更新跳数
end = maxPos;
step++;
}
}
}
cout << step << endl;
return 0;
}
算法分析与知识点:
本题主要运用贪心的思想,在具体的实现中,我们维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
实验题目:排队接水
题目描述:
夏天到了,又到了用水高峰期,偏巧小区的水管出了点问题,消防车赶紧给小区送了一车水过来。小区居民们纷纷拿出自家装水的容器,有的是个大塑料瓶,有的是茶水壶,有的是小塑料桶,哈哈,什么样的都有:)。现在有n个人在一个水龙头前排队接水,假设每个人接水的时间分别为Ti,请编程找出这n个人排队的一种顺序,使得这n个人的平均等待时间最小。
输入要求:
输入有多组测试数据
每组测试数据共两行,第一行为一个整数n,表示有n个人;
第二行分别表示第1个人到第n个人每人的接水时间T1,T2,…Tn。
输出要求:
输出文件有两行,第一行为一种排队顺序,即编号从1到n的n个人的一种排序方式;
第二行为这种排序方案下的平均等待时间(输出结果精确到小数点后两位)。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
struct person // 定义居民结构体,记录到来顺序及接水时间
{
int id, time;
};
person p[1000];
bool cmp(person p1, person p2) { // 自定义结构体排序方法
return p1.time < p2.time;
}
int main() {
int n;
while (cin >> n) {
for (int i = 0;i < n;i++) {
p[i].id = i;
cin >> p[i].time;
}
sort(p, p + n, cmp); // 按接水时间升序
double ans = 0;
for (int i = 0;i < n - 1;i++) {
cout << p[i].id + 1 << " ";
ans += (n - 1 - i) * p[i].time;
}
cout << p[n - 1].id + 1 << endl;
printf("%.2f\n", ans / n);
}
return 0;
}
算法分析与知识点:
本题主要运用贪心的思想,共有n名居民,他们所需的接水时间分别为 ,设他们的排队顺序为 ,可得出总共等待时间为
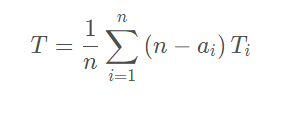
由以上公式可得要使得总的排队等待时间最短,就要按接水所需时间从小到大的顺序老排队接水。
贪心-堂练
实验题目: 区间问题1
题目描述:
给出n个区间的起点和终点,求最少使用其中多少个区间可以将所有区间所在的区域完全覆盖。(测试的数据确保这1点)。
输入要求:
第1行一个整数n,表示n个区间;
第2行开始n行,每行2个整数,表示一个区间范围。
类似[1,4] [5,6]被认为是覆盖了[1,6]。
输出要求:
从起点开始,按区间先后顺序,输出选中的区间。所选的区间应尽可能向终点扩展。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
struct part//区间两端
{
int star1, end1;
};
bool cmp(part s1, part s2) { // 自定义排序方式1、开始点升序,2、结束点升序
if (s1.star1 < s2.star1)
return true;
else if (s1.star1 == s2.star1 && s1.end1 < s2.end1)
return true;
else
return false;
}
int main()
{
part a[100];//全部待选区间
part r[100];
//在a中选好的数放入r中
int n, index = 0, i;
cin >> n;
for (i = 0; i < n; i++) {
cin >> a[i].star1 >> a[i].end1;
}
sort(a, a + n, cmp);
int right = a[0].star1 - 1;
int end = a[n - 1].end1; // 待覆盖区间最远处
for (i = 0; i < n - 1; )
{
int maRight = a[i].end1, maIndex = i;
while (a[i].star1 <= right + 1 && i < n) { // 寻找最远子区间
if (a[i].end1 > maRight) {
maRight = a[i].end1;
maIndex = i;
}
i++; //比较完数组往后移
}
right = maRight;
r[index++] = a[maIndex];
i = maIndex;
if (right == end)
break;
}
for (i = 0; i < index; i++) {
cout << r[i].star1 << " " << r[i].end1 << endl;
}
return 0;
}
算法分析与知识点:
思路:设置一个a[]数组保存原始的数据,设置一个人r[]数组保存被选的区间数据。
先按1、开始点升序,2、结束点升序将数据排序。为了使覆盖总区间的所需的子区间数最少,就要选出一系列覆盖范围最广的子区间。方式描述如下所示:初始令所能到达的范围为 ,然后选出一个子区间让这个范围尽可能向区间终点靠,即找到符合条件 的最远子区间。
实验题目:种树
题目描述:
一条街的一边有几座房子。因为环保原因居民想要在路边种些树,路边的地区被分割成块,并被编号成1…N;每个部分为一个单位尺寸大小并最多可种一棵树,每个居民想在门前种些树并指定了三个号码B,E,T,这三个数表示该居民想在B和E之间最少种T棵树。当然,B≤E,居民必须记住在指定区不能种多于区域地块数的树,所以T≤E-B+l。居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量。
输入要求:
第一行包含数据N,区域的个数;
第二行包含H,房子的数目;
下面的H行描述居民们的需要:B E T。
输出要求:
输出能满足所有要求的最少的树的数。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
int n, m, k, ans;
struct node // 保存要求数据
{
int b, e, t;
}a[5005];
bool used[30005]; // 记录该位置是否种过树
bool cmp(const node& a, const node& b) // 自定义排序方式
{
return a.e < b.e;
}
int main()
{
cin >> n >> m;
for (int i = 0;i < m;i++) // 输入数据
{
cin >> a[i].b >> a[i].e >> a[i].t;
}
sort(a, a + m, cmp);
memset(used, 0, sizeof(used)); //初始化每个位置都没种过树
ans = 0; // 记录所需树的数量
for (int i = 0;i < m;i++)
{
k = 0;
for (int j = a[i].b;j <= a[i].e;j++) // 求在该要求区间内已经种了多少树
{
if (used[j]) k++;
}
if (k >= a[i].t) // 未达到要求
continue;
k = a[i].t - k; // 还要种的数量
for (int j = a[i].e;j >= a[i].b;j--)
{
if (used[j] == false) // 寻找没种过的位置
{
used[j] = true;//种树
ans++;
k--;
}
if (k == 0)
break;
}
}
cout << ans << endl;
return 0;
}
算法分析与知识点:
本题采用贪心算法的思想,要使所需的总树苗数量最小,就要让一个区间的树苗将可能的能满足更多的用户要求。这里采用让后面的居民尽可能为前面的居民着想,即在满足自己要求的前提下把树尽可能地往前面的位置种,这样可以让居民的要求重叠的范围更多,从而达到使用最少的树苗满足所有居民的要求。
为了达到目的,我们需要先将居民按提出要求的开始区间点排序,然后从后往前尽可能地为前面地居民考虑。考虑满足第i个居民方式:要先考虑满足第i+1个居民的要求后里自己的要求还差多少,然后由于为第i-1个居民着想的目的,将未满足要求的树苗种在第i个居民要求区间的前面。
实验题目:智力大冲
题目描述:
小伟报名参加中央电视台的智力大冲浪节目,本次挑战赛吸引了众多参赛者,主持人为了表彰大家的勇气,先奖励每个参赛者m元。先不要太高兴!因为这些钱还不一定都是你的!接下来主持人宣布了比赛规则:
首先,比赛时间分为n个时段(n≤500),它又给出了很多小游戏,每个小游戏都必须在规定期限ti前完成(1≤ti≤n)。如果一个游戏没能在规定期限前完成,则要从奖励费m元中扣去一部分钱wi,wi为自然数,不同的游戏扣去的钱是不一样的。当然,每个游戏本身都很简单,保证每个参赛者都能在一个时段内完成,而且都必须从整时段开始。主持人只是想考考每个参赛者如何安排组织自己做游戏的顺序。作为参赛者,小伟很想赢得冠军,当然更想赢取最多的钱!注意:比赛绝对不会让参赛者赔钱!
输入要求:
输入文共4行。
第1行为m,表示一开始奖励给每位参赛者的钱
第2行为n,表示有n个小游戏;
第3行有n个数,分别表示游戏1到n的规定完成期限;
第4行有n个数,分别表示游戏1到n不能在规定期限前完成的扣款数。
输出要求:
输出仅1行,表示小伟能赢取最多的钱。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int n, m, f[N];
struct node {
int t, w;
}a[N];
int cmp(node x, node y) { return x.w > y.w; } // 自定义排序方式
void work()
{
sort(a + 1, a + 1 + n, cmp);
for (int i = 1;i <= n;i++)
{
bool pd = false; // 判断该游戏是否被完成
for (int j = a[i].t;j >= 1;j--)
{
if (f[j] == 0) //可以安排这个游戏
{
f[j] = 1;
pd = true;
break;
}
}
if (pd == false) m -= a[i].w;
}
}
int main()
{
cin >> m >> n;
for (int i = 1;i <= n;i++) cin >> a[i].t;
for (int i = 1;i <= n;i++) cin >> a[i].w;
work();
cout << m << endl;
return 0;
}
算法分析与知识点:
本题采用贪心算法的思想,首先将所有游戏按其价值从高到低排序。一个游戏只要在规定期限完成之前完成就不会被扣除奖励,为了让一个游戏尽可能不影响其他游戏,我们让其在自己的规定期限内尽可能地往后靠。我们从奖励价值最高的游戏开始考虑,将所有游戏考虑完成后就可以得到的所获得的奖励最大值。
实验题目:删除数字II
题目描述:
在给定的n个数字的数字串m中,删除其中k(k< n)个数字后,剩下的数字按原次序组成一个新的整数。请确定删除方案,使得剩下的数字组成的新整数最小。(1<=k<n<=240)
输入要求:
输入有一行,先输入数字串m,再输入k,如描述所示。
保证数字串m没有前导0。
输出要求:
输出有两行,第一行按顺序输出从左到右删除的k个数字,用空格隔开。(第一行里的输出顺序是按照被删除数字在原数中的顺序排列的,而不是按照删除的顺序排列的)
第二行输出删除k个数字后剩下的数字组成的新数,并换行。
实验代码及注释:
#include <bits/stdc++.h>
using namespace std;
struct node // 记录被删除数字的内容及下标
{
char c;
int index;
}temp[300];
bool cmp(node a, node b) { // 自定义排序方式
return a.index < b.index;
}
int main()
{
string s, t;
int k;
vector<int> index; //下标数组
cin >> s >> k;
for (int i = 0;i < s.length();i++) //初始化下标数组
index.push_back(i);
for (int i = 0;i < k;i++) {
int j;
for (j = 0;j < s.length() - 1;j++) { // 寻找要删除哪个数字
if (s[j] > s[j + 1]) {
break;
}
}
temp[i].c = s[j]; // 记录被删除数字的内容
temp[i].index = index[j]; // 记录被删除数字在原数字中的位置
s.erase(j, 1);
index.erase(index.begin() + j);
}
sort(temp, temp + k, cmp);//将删除的数字按其在原数字中的位置排序
for (int i = 0;i < k - 1;i++)
cout << temp[i].c << " ";
cout << temp[k - 1].c << endl;
while (s[0] == '0')
s.erase(0, 1);
if (s.length() == 0)
s = "0";
cout << s << endl;
return 0;
}
算法分析与知识点:
本题采用贪心算法的思想,要删除k个数字的中的数字字符串后数字最大,就要让每次删除一个字符后留下来的数字都要是当下的最小值。
为了找到一个字符,将其删除后让留下来的数字最小,被删除的数字要满足条件如下:
从数字字符串从高位到低位第一个变小的数字。

上述数字的第一次删除就应该删除数字8.
加载全部内容