Python队列
姜学迁 人气:0模拟打印机任务队列过程
计算机科学中也有众多的队列例子。比如计算机实验室有10台计算机,它们都与同一台打印机相连。当学生需要打印的时候,他们的打印任务会进入一个队列。该队列中的第一个任务就是即将执行的打印任务。如果一个任务排在队列的最后面,那么它必须等到所有前面的任务都执行完毕后才能执行。
学生向共享打印机发送打印请求,这些打印任务被存在一个队列中,并且按照先到先得的顺序执行。这样的设定可能导致很多问题。其中最重要的是,打印机能否处理一定量的工作。如果不能,学生可能会由于等待过长时间而错过要上的课。
考虑计算机实验室里的这样一个场景:在任何给定的一小时内,实验室里都有10个学生。他们在这 一小时内最多打印2次,并且打印的页数从1到20页不等。实验室的打印机比较老旧,每分钟只能以低质量打印10页。也可以将打印质量调高,但是这样做会导致打印机每分钟只能打印5页。降低打印速度可能导致学生等待过长时间。那么,应该如何设置打印速度呢?
可以通过构建一个模型来解决该问题。我们需要为学生、打印任务和打印机构建对象。当学生提交打印任务时,我们需要将它们加入打印机的任务队列中。当打印机执行完一个任务后,它会检查该队列,看看其中是否还有需要处理的任务。我们感兴趣的是学生平均需要等待多久才能拿到打印好的文章。这个时间等于打印任务在队列中的平均等待时间。
在模拟时,需要应用一些概率学知识。举例来说,学生打印的文章可能有1~20页。如果各页数出现的概率相等,那么打印任务的实际时长可以通过模拟1~20的一个文章页数随机数来计算得出。
如果实验室里有10个学生,并且在一小时内每个人都打印两次,那么每小时平均就有20个打印任务。 在任意一秒,创建一个打印请求的概率是多少? 回答这个问题需要考虑任务与时间的比值。每小时20个任务相当于每180秒1个任务。
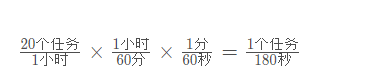
可以通过1~180的一个随机数来模拟每秒内产生打印请求的概率(1/180的概率)。如果随机数正好是180,那么就认为有 一个打印请求被创建。注意,可能会出现多个请求接连被创建的情况,也可能很长一段时间内都没有请求。这就是模拟的本质。我们希望在常用参数已知的情况下尽可能准确地模拟。
主要模拟步骤:
1.创建一个打印任务队列。每一个任务到来时都会有一个时间戳。一开始,队列是空的。
2.针对每一秒(currentSecond),执行以下操作。
- 是否有新创建的打印任务?如果是,以 currentSecond 作为其时间戳并将该任务加入到队列中。
- 如果打印机空闲,并且有正在等待执行的任务,执行以下操作:
- 从队列中取出第一个任务并提交给打印机;
- 用 currentSecond 减去该任务的时间戳,以此计算其等待时间;
- 将该任务的等待时间存入一个列表,用来作为计算平均等待时间的数据;
- 根据该任务的页数,计算执行时间。
- 打印机进行一秒的打印,同时从该任务的执行时间中减去一秒。
- 如果打印任务执行完毕,即任务的执行时间减为0,则说明打印机回到空闲状态。
3.当模拟完成之后,根据等待时间列表中的值计算平均等待时间。
构建队列程序
class Queue:
def __init__(self):
self.items = [] # 构建空队列
def isEmpty(self):
return self.items ==[] # 判断是否为空
def enqueue(self,item):
self.items.insert(0, item) # 在队列尾部(列表左端)插入元素
def dequeue(self):
return self.items.pop() # 在队列头部(列表右端)移出元素
def size(self):
return len(self.items) # 队列(列表)长度
模拟打印程序
import random
# 模拟打印机
class Printer:
# 打印机初始化
def __init__(self, ppm):
self.pagerate = ppm # 打印速度 页/分钟
self.currentTask = None # 现有任务
self.timeRemain = 0 # 该任务所需时间
# 打印任务倒计时 0代表打印完成
def tick(self):
# 如果打印机正在执行任务
if self.currentTask != None:
# 该任务执行时间 = 执行时间 - 1(执行时间倒计时)
self.timeRemaining = self.timeRemaining - 1
if self.timeRemaining <= 0: # 该任务执行时间 <= 0
self.currentTask = None # 该任务执行完毕
# 判断打印机是否空闲
def busy(self):
if self.currentTask != None:
return True
else:
return False
# 打印机接受新任务
def startNext(self, newtask):
self.currentTask = newtask
# 新打印任务需要时间 = 新任务页数 * (60 / 每分钟打印多少页的速度)
# (60 / 每分钟打印多少页的速度) = 每打印一页所需要的秒数
self.timeRemaining = newtask.getPages() * (60 / self.pagerate)
# 模拟单个任务的属性
class Task:
# 任务初始化
def __init__(self, time):
self.timestamp = time # 创建任务的时间点
self.pages = random.randrange(1, 21) # 任务页数 在 1~20 间随机生成
def getStamp(self):
return self.timestamp # 获取任务创建的时间点
def getPages(self):
return self.pages # 获取任务的页数
def waitTime(self, currenttime):
# 任务的等待时间 = 当前时间 - 任务创建的时间点
return currenttime - self.timestamp
# 模拟学生创建的新打印请求
def newPrintTask():
# 打印请求是一个随机事件
# 通过1~180之间的一个随机数来模拟每秒内产生打印请求的概率
# 如果随机数正好是180,那么就认为有一个打印请求被创建。
num = random.randrange(1, 181)
if num == 180:
return True
else:
return False
# 模拟打印过程
def simulation(numSeconds, pagesPerMinute):
labprinter = Printer(pagesPerMinute)
printQueue = Queue()
waitingtimes = []
for currentSecond in range(numSeconds):
if newPrintTask():
task = Task(currentSecond)
printQueue.enqueue(task)
if(not labprinter.busy())and(not printQueue.isEmpty()):
nexttask = printQueue.dequeue()
waitingtimes.append(nexttask.waitTime(currentSecond))
labprinter.startNext(nexttask)
labprinter.tick()
averageWait = sum(waitingtimes)/len(waitingtimes)
print("平均等待 %6.2f 秒,还有 %3d 个任务等待处理"
% (averageWait, printQueue.size()))
模拟打印过程(有注释)
def simulation(numSeconds, pagesPerMinute):
# numSeconds-时间段
# pagesPerMinute-打印速度,页/分钟
labprinter = Printer(pagesPerMinute) # 创建打印机
printQueue = Queue() # 创建打印机任务队列
waitingtimes = [] # 创建等待时间数据样本列表
for currentSecond in range(numSeconds): # 一次循环代表一秒
if newPrintTask(): # 如果 有打印请求创建
task = Task(currentSecond) # 创建打印任务并记录当前时间点
printQueue.enqueue(task) # 打印任务进入打印机任务队列
# 如果 打印机空闲 并且 打印机任务队列有任务
if(not labprinter.busy())and(not printQueue.isEmpty()):
nexttask = printQueue.dequeue() # 从队列取出新任务
# 根据当前时间点计算新任务在任务队列里的等待时间 并将等待时间记录进样本列表
waitingtimes.append(nexttask.waitTime(currentSecond))
labprinter.startNext(nexttask) # 开始执行新任务 打印机进入忙碌状态
labprinter.tick() # 每循环一次 当前打印任务执行倒计时减少一秒
averageWait = sum(waitingtimes)/len(waitingtimes)
print("平均等待 %6.2f 秒,还有 %3d 个任务等待处理" % (averageWait, printQueue.size()))
需要注意的是,时间戳是我们根据循环模拟出来的,我们给定了 numSeconds 时间段后,每循环一次相当于时间过了一秒。
虽然每次模拟的结果不一定相同。但对此我们不需要在意。这是由于随机数的本质导致的。我们感兴趣的是当参数改变时结果出现的趋势。
下面是一些结果:

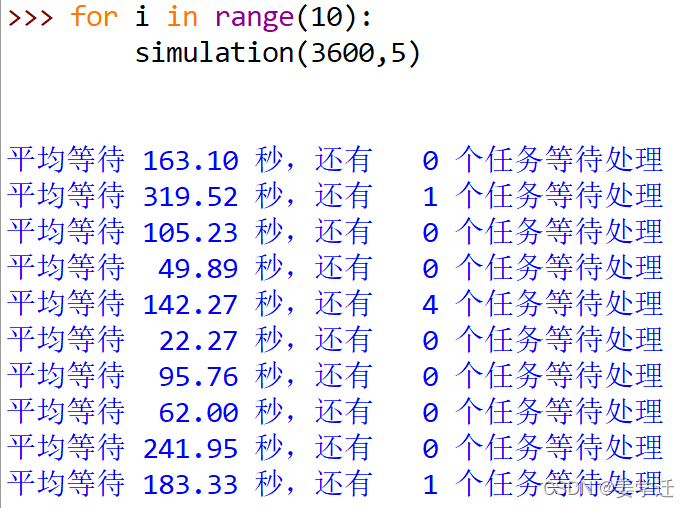
我们根据模拟得到了打印机在两种速度下,一小时内的任务执行情况的参考数据。可以很明显的看到,当打印质量提升后,学生平均等待时间相比低质量情况下显著增加,并且任务处理未完成的次数也出现了增加,所以设置打印机为低质量模式是最合适的。
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注的更多内容!
加载全部内容