C++ 动态规划

时间:2022-05-28 ymz123_ 人气:0

Fibonacci

题目描述：

大家都知道斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项。

解题思路：

1.递归

2.动态规划

状态：F(n)

状态递推：F(n)=F(n-1)+F(n-2)

初始值：F(1)=F(2)=1

返回结果：F(N)

代码实现：

法一：递归（效率低）：

class Solution{public: int Fibonacci(int n)
{        // 初始值 
	if (n <= 0)
	{ 
		return 0; 
	} 
	if (n == 1 || n == 2) 
	{
		return 1; 
	}        
	// F(n)=F(n-1)+F(n-2) 
	return Fibonacci(n - 2) + Fibonacci(n - 1); }};

法二：动态规划

class Solution {
public:
    int Fibonacci(int n) {
        if(n==1 || n==2)
            return 1;
        int fn;
        int fn1 = 1, fn2 = 1;
        for(int i = 2; i < n; i++)
        {
            fn = fn1 + fn2;
            fn1 = fn2;
            fn2 = fn;
        }
        
        return fn;
        /*上述解法的空间复杂度为O(n)
        其实F(n)只与它相邻的前两项有关，
        所以没有必要保存所有子问题的解
        只需要保存两个子问题的解就可以
        下面方法的空间复杂度将为O(1)*/
        if(n==1 || n==2)
            return 1;
        int* F = new int[n];
        //初始状态
        F[0] = 1;
        F[1] = 1;
        for(int i = 2; i < n; i++)
        {
            F[i] = F[i-1] + F[i-2];
        }
        
        return F[n-1];
    }
};

字符串分割(Word Break)

题目描述：

给定一个字符串s和一组单词dict，判断s是否可以用空格分割成一个单词序列，使得单词序列中所有的单词都是dict中的单词（序列可以包含一个或多个单词）。

例如:

给定s=“nowcode”；

dict=[“now”, “code”].

返回true，因为"nowcode"可以被分割成"now code".

解题思路：

状态：

子状态：前1，2，3，…,n个字符能否根据词典中的词被成功分词
F(i): 前i个字符能否根据词典中的词被成功分词

状态递推：

F(i): true{j <i && F(j) && substr[j+1,i]能在词典中找到} OR false 在j小于i中，只要能找到一个F(j)为true，并且从j+1到i之间的字符能在词典中找到，则F(i)为true

初始值：

对于初始值无法确定的，可以引入一个不代表实际意义的空状态，作为状态的起始空状态的值需要保证状态递推可以正确且顺利的进行，到底取什么值可以通过简单的例子进行验证 F(0) = true

返回结果：F(n)

代码实现：

class Solution {
public:
    bool wordBreak(string s, unordered_set<string> &dict) {
        int len = s.size();
        vector<bool> F(len+1, false);
        F[0] = true;
        for(int i = 1; i <= len; i++)
        {
            //F[8]的状态：7<8 && F[7] && [8,8]
            //F[8]的状态：6<8 && F[6] && [7,8] 
            for(int j = i-1; j >= 0; j--)
            {
                if(F[j] && dict.find(s.substr(j,i-j)) != dict.end())
                {
                    F[i] = true;
                    break;
                }
            }
        }
        
        return F[len];
    }
};

三角矩阵(Triangle)

题目描述：

给出一个三角形，计算从三角形顶部到底部的最小路径和，每一步都可以移动到下面一行相邻的数字

例如，给出的三角形如下：

[[20],[30,40],[60,50,70],[40,10,80,30]]

解题思路：

状态：子状态：从(0,0)到(1,0),(1,1),(2,0),…(n,n)的最短路径和 F(i,j): 从(0,0)到(i,j)的最短路径和

状态递推： F(i,j) = min( F(i-1, j-1), F(i-1, j)) + triangle[i][j]

初始值： F(0,0) = triangle[0][0]返回结果： min(F(n-1, i))

代码实现：

class Solution {
public:
    int minimumTotal(vector<vector<int> > &triangle) {
        if(triangle.empty())
            return 0;
        int row = triangle.size();
        vector<vector<int> > minSum(triangle);
        for(int i = 1; i < row; i++)
        {
            for(int j = 0; j <= i; j++)
            {
                if(j == 0)
                    minSum[i][j] = minSum[i-1][j] + triangle[i][j];
                else if(j == i)
                    minSum[i][j] = minSum[i-1][j-1] + triangle[i][j];
                else
                    minSum[i][j] = min(minSum[i-1][j], minSum[i-1][j-1])
                                   + triangle[i][j];
            }
        }
        int result = minSum[row-1][0];
        for(int i = 1; i < triangle.size(); i++)
        {
            result = min(result, minSum[row-1][i]);
        }
        
        return result;
    }
};

路径总数(Unique Paths)

题目描述：

一个机器人在m×n大小的地图的左上角（起点）。机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。可以有多少种不同的路径从起点走到终点？

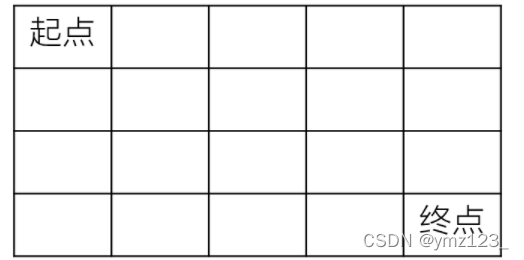
解题思路：

状态：子状态：从(0,0)到达(1,0),(1,1),(2,1),…(m-1,n-1)的路径数 F(i,j): 从(0,0)到达F(i,j)的路径数

状态递推： F(i,j) = F(i-1,j) + F(i,j-1)

初始化：特殊情况：第0行和第0列 F(0,i) = 1 F(i,0) = 1

返回结果： F(m-1,n-1)

代码实现：

class Solution {
public:
    /**
     * 
     * @param m int整型 
     * @param n int整型 
     * @return int整型
     */
    int uniquePaths(int m, int n) {
        // write code here
        vector<vector<int> > ret(m, vector<int>(n,1));
        for(int i = 1; i < m; i++)
        {
            for(int j = 1; j < n; j++)
            {
                ret[i][j] = ret[i-1][j] + ret[i][j-1];
            }
        }
        
        return ret[m-1][n-1];
    }
};

最小路径和(Minimum Path Sum)

题目描述：

给定一个由非负整数填充的m x n的二维数组，现在要从二维数组的左上角走到右下角，请找出路径上的所有数字之和最小的路径。注意：你每次只能向下或向右移动。

解题思路：

状态：子状态：从(0,0)到达(1,0),(1,1),(2,1),…(m-1,n-1)的最短路径 F(i,j): 从(0,0)到达F(i,j)的最短路径。

状态递推： F(i,j) = min{F(i-1,j) , F(i,j-1)} + (i,j)

初始化： F(0,0) = (0,0) 特殊情况：第0行和第0列 F(0,i) = F(0,i-1) + (0,i) F(i,0) = F(i-1,0) + (i,0)

返回结果： F(m-1,n-1)

代码实现：

class Solution {
public:
    /**
     * 
     * @param grid int整型vector<vector<>> 
     * @return int整型
     */
    int minPathSum(vector<vector<int> >& grid) {
        // write code here
        if(grid.size() == 0 || grid[0].size() == 0)
            return 0;
        int M = grid.size();
        int N = grid[0].size();
        vector<vector<int> > ret(M, vector<int>(N,0));
        ret[0][0] = grid[0][0];
        for(int i = 1; i < N; i++)
        {
            ret[0][i] = ret[0][i-1] + grid[0][i];
        }
        for(int i = 1; i < M; i++)
        {
            ret[i][0] = ret[i-1][0] + grid[i][0];
        }
        for(int i = 1; i < M; i++)
        {
            for(int j = 1; j < N; j++)
            {
                ret[i][j] = min(ret[i-1][j],ret[i][j-1]) + grid[i][j];
            }
        }
        
        return ret[M-1][N-1];
    }
};

加载全部内容