Java 二叉树

时间:2022-05-28 Pretend.. 人气:0

二叉树操作的代码大多数使用递归来实现，代码会比较简洁，如果使用非递归，代码会比较的繁荣，而且不易理解。（上）中的题偏向于基础，后面（下）中的题机会比较难。

1、二叉树的遍历

（1）前、中、后序遍历

这里写到的遍历是递归遍历，代码比较简单，后续会写非递归的代码。以前序遍历为例：

如果根节点root为空，直接返回，否则，打印根节点，再分别递归root的左子树和右子树即可。中序遍历的话，先中序遍历左子树，打印根节点，再中序遍历右子树即可。

【代码如下】

//递归实现，比较简单
public void preTree(Node root){
        if(root==null){
            return;
        }
        System.out.print(root.val+" ");
        preTree(root.left);
        preTree(root.right);
    }

（2）层序遍历

【OJ链接】

OJ的返回值为一个存放链表的链表，所以我们可以将每一层的元素存放在同一个链表中，作为元素存放在要返回的链表中。还是使用队列来遍历链表，每次出根节点，当其左右节点不为空的时候，入左右节点。直到队列为空，遍历完成。

如何判断二叉树每层结点的个数？

在对每层节点出队完成后，队列中剩余结点的个数就是下一层结点的个数。比如：现在给队列如跟节点，队列大小为1，第一层的节点个数就为1；当根节点出对后，我们需要入队根节点的左右节点，如果左节点为null，则只入右节点，此时队列大小为1，第二层的节点个数就为1。

【代码如下】

public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret=new ArrayList<>();
        if(root==null){
            return ret;
        }
        Queue<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            List<Integer> list=new ArrayList<>();
            int size=queue.size();
            while(size--!=0){
                TreeNode node=queue.poll();
                list.add(node.val);
                if(node.left!=null){
                    queue.offer(node.left);
                }
                if(node.right!=null){
                    queue.offer(node.right);
                }
            }
            ret.add(list);
        }
        return ret;
    }

2、获取树中子结点的个数

通常二叉树的问题，都会有两种思路：遍历思路和子问题思路。

如这道题：

我们可以求出它的左子树和右子树中子结点的个数，相加即可；或者，定义计数器，因为要递归，所以我们需要一个全局变量（count），递归左右子树，只要遇到子节点，count就加一。

【代码如下】

//获取叶子节点的个数
    //方法一
    public int getLeafNodeCount1(Node root){
        if(root==null){
            return 0;
        }
        if(root.left==null&&root.right==null){
            return 1;
        }
        return getLeafNodeCount1(root.left)+getLeafNodeCount1(root.right);
    }
    // 方法二
    public static int count1;
    public void getLeafNodeCount2(Node root){
        if(root==null){
            return ;
        }
        if(root.left==null&&root.right==null){
            count1++;
        }
        getLeafNodeCount2(root.left);
        getLeafNodeCount2(root.right);
    }

3、获取二叉树的高度

获取二叉树的高度，我们只需要获取二叉树左右子树的高度，返回左右子树的最大高度加一即可。

【代码如下】

 // 获取二叉树的高度
    public int getHeight(Node root){
        if(root==null){
            return 0;
        }
        int left=getHeight(root.left);
        int right=getHeight(root.right);
        return left>right?left+1:right+1;
    }

4、判断是不是完全二叉树

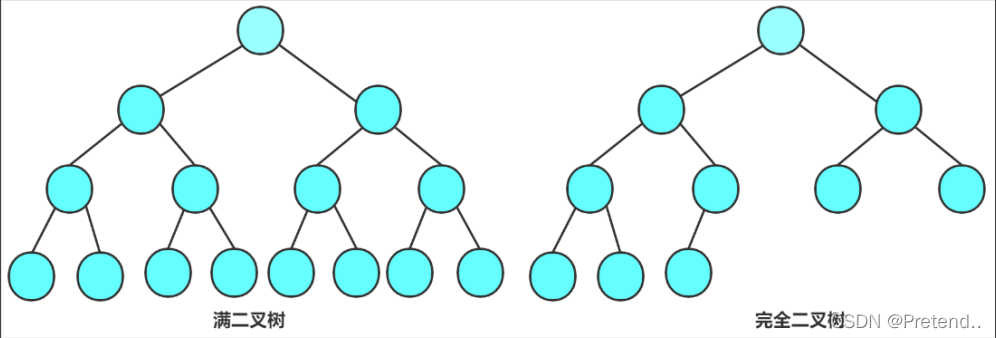
【完全二叉树和满二叉树】

满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵二叉树的层数为K，且结点总数是 2^K-1，则它就是满二叉树。
完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

判断完全二叉树，我们可以借助队列来实现，在二叉树不为空的情况下，对二叉树进行层序遍历：定义一个队列，将根节点放入，只要队列不为空，进行出队，将得到的节点的左右节点入队，注意先左后右，节点为空也要进行入队（队列可以存储null）。直到遇到第一个出队的节点为null，对队列中剩下的元素进行遍历，如果全为null，则为完全二叉树；如果存在不为null的结点，则不是完全二叉树。

 public boolean isCompleteTree(Node root){
       Queue<Node> queue=new LinkedList<>();
       queue.offer(root);
       //如果队列为空，会存在空指针异常
       while(!queue.isEmpty()){
           //层序遍历
           Node node=queue.poll();
           if(node!=null){
               //将节点的左右子节点放入队列
               queue.offer(node.left);
               queue.offer(node.right);
           }else{
               //如果node为null，直接对队列进行判断
               break;
           }
       }
       int x=queue.size();
       //判断队列元素是否全为null
       for(int i=0;i<x;++i){
           if(queue.poll()!=null){
               return false;
           }
       }
       return true;
    }

5、判断两个树是否相同

【OJ链接】

存在以下四种情况：

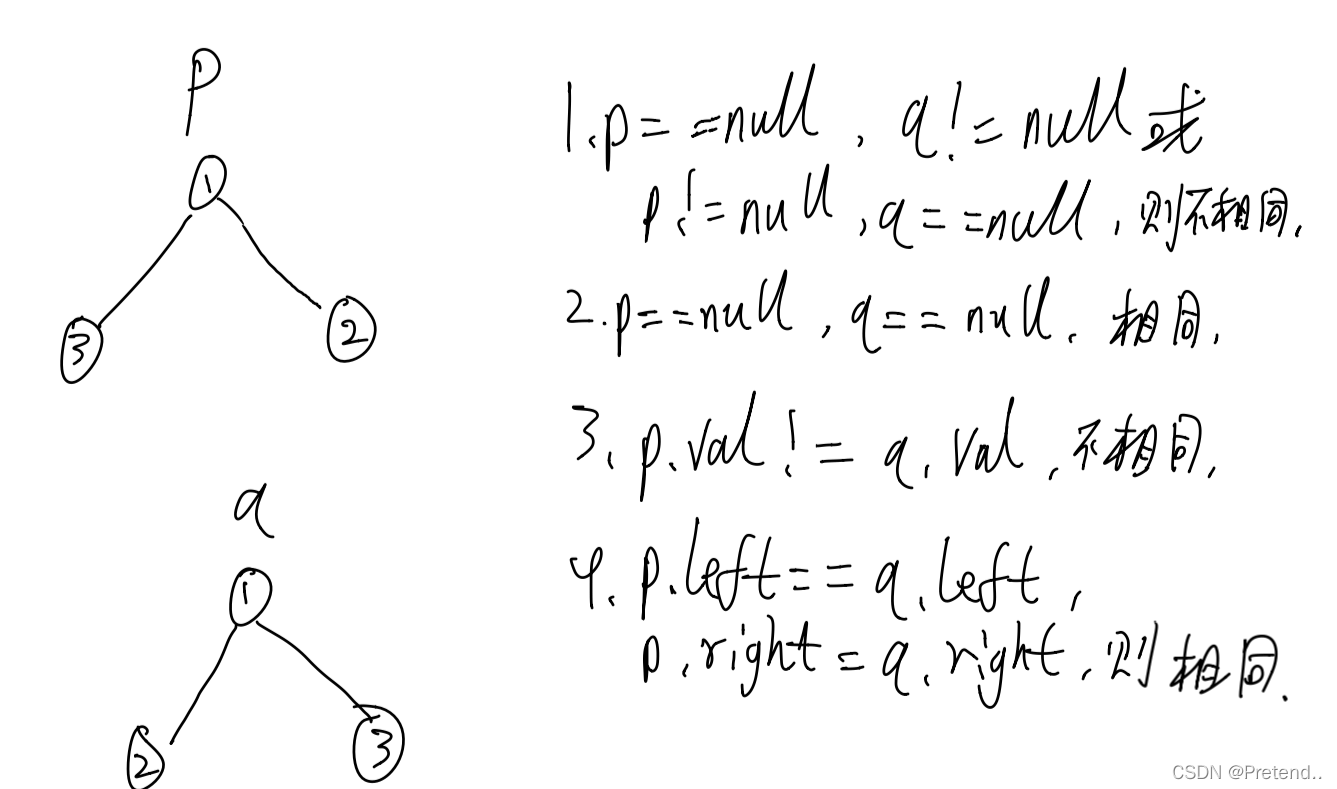
【代码如下】

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p==null&&q!=null||p!=null&&q==null){
            return false;
        }
        if(p==null&&q==null){
            return true;
        }
        if(p.val!=q.val){
            return false;
        }
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }
}

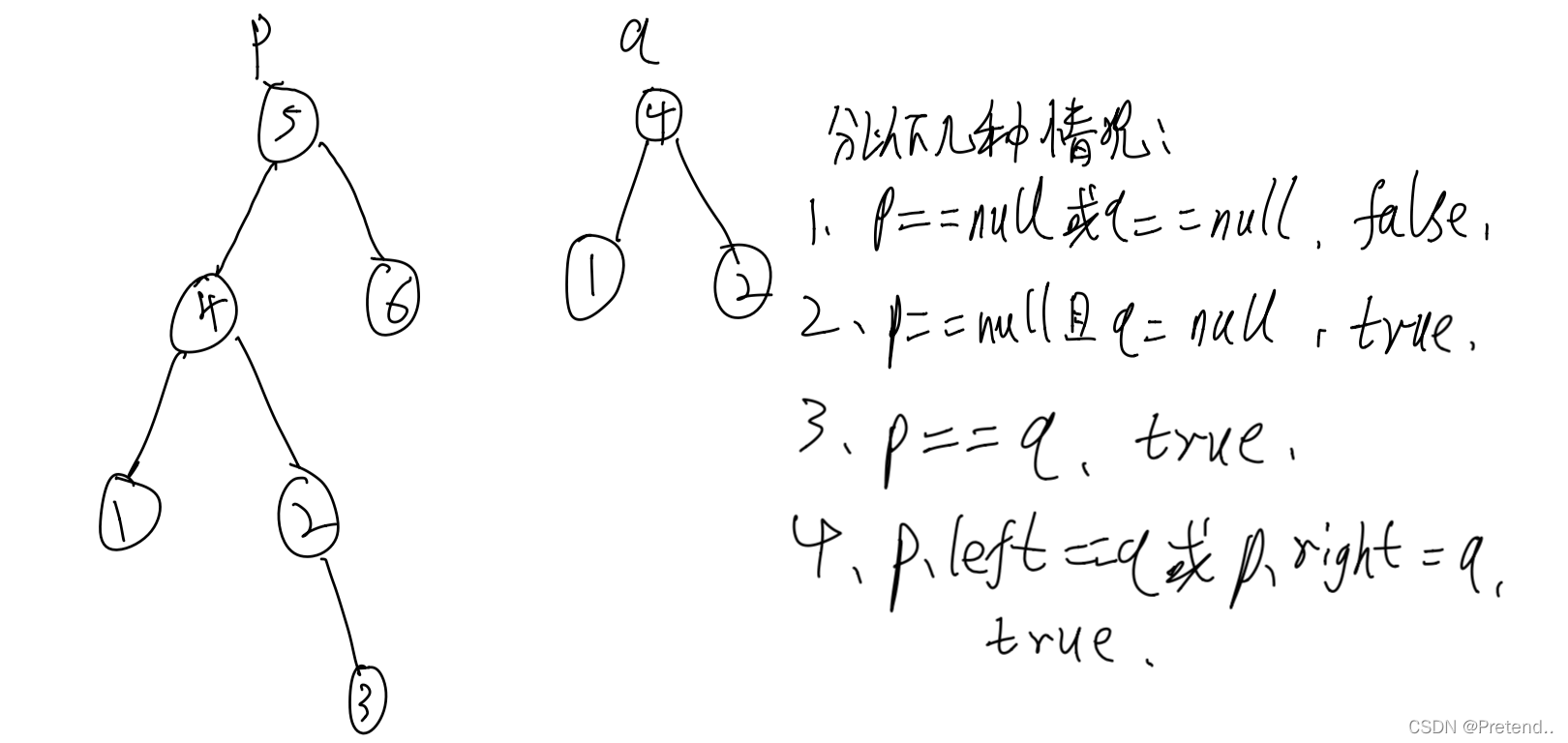
6、另一棵树的子树

【OJ链接】

上面已经给写过判断两棵树是否相等的题，我们只需要判断树p是否等于树q，或者数p的左子树或右子树是否等于树q。分为以下几种情况：

【代码如下】

class Solution {
    //判断两个树是否相等
    public boolean isSameTree(TreeNode root,TreeNode subRoot){
        if(root==null&&subRoot!=null||root!=null&&subRoot==null){
            return false;
        }
        if(root==null&&subRoot==null){
            return true;
        }
        if(root.val!=subRoot.val){
            return false;
        }
        return isSameTree(root.left,subRoot.left)&&isSameTree(root.right,subRoot.right);
    }
    //判断子树
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root==null||subRoot==null){
             return false;
        }
        if(isSameTree(root,subRoot)){
            return true;
        }
        return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot);
    }
}

7、判断平衡二叉树

【OJ链接】

高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

首先我们需要写一个函数来求二叉树的高度，只要这个二叉树的左右子树高度差不大于1，且左右子树都是平衡二叉树，则其为平衡二叉树。

【代码如下】

class Solution {
    //求二叉树的高度
    public int maxDepth(TreeNode root){
        if(root==null){
            return 0;
        }
        int left=maxDepth(root.left);
        int right=maxDepth(root.right);
        return left>right?left+1:right+1;
    }
    //判断二叉树是不是平衡二叉树
    public boolean isBalanced(TreeNode root) {
        if(root==null){
            return true;
        }
        if(Math.abs(maxDepth(root.left)-maxDepth(root.right))<=1){
            return isBalanced(root.left)&&isBalanced(root.right);
        }
        return false;
    }
}

加载全部内容