Java 数据结构
撩得Android一次心动 人气:1一.bfs
bfs(广度优先搜索),类似二叉树的层序遍历,利用队列完成。一般用于求最短路。
图的最短路问题:
给定一个无向图,每条边的长度都是1。求1号点到x号点的最短距离。 顶点数n 边数为m
q次询问 输入x 输出1到x的最短距离。 若1号点到x不连通,则输出-1
二.双端队列
双端队列的应用(区间翻转):
对于长度为n的数组,给定一个长度为m的区间,区间初始位置为a[1]到a[m]。
3种操作:
- 区间右移(最右端不会超过a[n])
- 区间左移(最左端不会超过a[n])
- 区间内所有数翻转。
q次操作后请你还原数组。
三.算法题
1.kotori和迷宫
难度⭐⭐
知识点:bfs
首先找到k字母,然后从k字母位置开始bfs。bfs过程中即可得到k到每个e的最短路程。(要注意走过的e不可继续往下走)
题目描述:
kotori在一个n*m迷宫里,迷宫的最外层被岩浆淹没,无法涉足,迷宫内有k个出口。kotori只能上下左右四个方向移动。她想知道有多少出口是她能到达的,最近的出口离她有多远?
输入描述:
第一行为两个整数n和m,代表迷宫的行和列数 (1≤n,m≤30)
后面紧跟着n行长度为m的字符串来描述迷宫。'k'代表kotori开始的位置,'.'代表道路,'*'代表墙壁,'e'代表出口。保证输入合法。
输出描述:
若有出口可以抵达,则输出2个整数,第一个代表kotori可选择的出口的数量,第二个代表kotori到最近的出口的步数。(注意,kotori到达出口一定会离开迷宫)
若没有出口可以抵达,则输出-1。
示例1
输入
6 8
e.*.*e.*
.**.*.*e
..*k**..
***.*.e*
.**.*.**
*......e
输出
2 7
说明
可供选择坐标为[4,7]和[6,8],到kotori的距离分别是8和7步。
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
String[] s1 = bf.readLine().split(" ");
int n = Integer.parseInt(s1[0]);
int m = Integer.parseInt(s1[1]);
//建立地图、标记图
char[][] maze = new char[n][m];
boolean[][] visited = new boolean[n][m];
//纪录步数
int[][] dis = new int[n][m];
//纪录初始的坐标
int ki = 0, kj = 0;
for(int i = 0; i < n; i++){
String s = bf.readLine();
for(int j = 0; j < m; j++){
dis[i][j] = Integer.MAX_VALUE;
char c = s.charAt(j);
maze[i][j] = c;
if(c == 'k'){
ki = i;
kj = j;
}
}
}
int count = 0, min = Integer.MAX_VALUE;
Queue<Integer> queue = new ArrayDeque<>();
//二维数组的性质,保存了坐标,并且节省了空间
queue.add(ki * m + kj);
visited[ki][kj] = true;
dis[ki][kj]= 0;
while(!queue.isEmpty()){
int temp = queue.poll();
int tempi = temp / m, tempj = temp % m;
//支持八个方向的移动或者不移动(但是因为Math.abs(i - j) == 1限定了绝对值为1,所以变成了四个方向)
for(int i = -1; i <= 1; i++){
for(int j = -1; j <= 1; j++){
if(Math.abs(i - j) == 1 && tempi + i >= 0 && tempi + i < n && tempj + j >= 0 && tempj + j < m && !visited[tempi + i][tempj + j]){
if(maze[tempi + i][tempj + j] == '.'){
visited[tempi + i][tempj + j] = true;
dis[tempi + i][tempj + j] = dis[tempi][tempj] + 1;
queue.add((tempi + i) * m + (tempj + j));
}
if(maze[tempi + i][tempj + j] == 'e'){
visited[tempi + i][tempj + j] = true;
dis[tempi + i][tempj + j] = dis[tempi][tempj] + 1;
min = Math.min(min, dis[tempi][tempj] + 1);
count++;
}
}
}
}
}
if(count == 0) System.out.print(-1);
else System.out.print(count + " " + min);
}
}
思考:队列是怎么实现bfs的?
1.起始点入队-->2.将起始点四个方向的可达点入队-->3.起始点出队。以此循序依次访问队列中的元素。
2.小红找红点
难度⭐⭐⭐
知识点:bfs,多源最短路
多源最短路的求法:在bfs开始之前将所有点都扔进队列,然后开始bfs即可。
题目描述:
小红拿到了一张无向图,有 n 个顶点和 m 条边。每条边的长度为 1 。
小红给一些顶点染成了红色。她想知道,对于每个顶点,到附近最近的红色点的距离为多少?
输入描述:
第一行输出两个正整数 n 和 m ,用空格隔开。分别代表顶点数和边数。
第二行输入一个长度为 n 的字符串,代表每个顶点的染色情况。第 i 个字符为 'R' 代表被染成红色,为 'W' 代表未被染色。
接下来的 m 行,每行两个正整数 x 和 y ,代表 x 和 y 有一条无向边相连。
不保证图是整体连通的。不保证没有重边和自环。
1<=n,m<=10^5
输出描述:
输出一行 n 个整数,代表从 1 到 n 每个顶点到最近的红色顶点的距离。若对于某点而言无论如何都走不到红色顶点,则输出 -1 。
示例1:
输入
5 5
RWWRW
1 2
3 3
1 2
2 5
1 4
输出
0 1 -1 0 2
说明
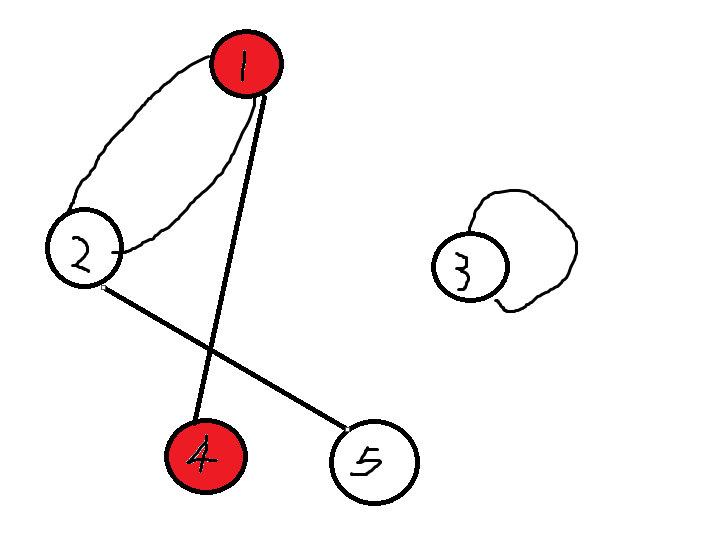
样例的图如上所示。
import java.util.*;
import java.io.*;
public class Main{
static ArrayList<Integer>[] g;
static String[] strings;
static int[] visited;
static int[] dis;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] firstLine = br.readLine().split(" ");
int n = Integer.parseInt(firstLine[0]);
int m = Integer.parseInt(firstLine[1]);
g = new ArrayList[n+1];
visited = new int[n+1];
dis= new int[n+1];
for (int i=1;i<n+1;i++) {
g[i] = new ArrayList<Integer>();
}
//一个字符一个字符的读取
strings = br.readLine().split("");
for (int i=0;i<m;i++) {
//描绘双向图
String[] temp = br.readLine().split(" ");
int x = Integer.parseInt(temp[0]);
int y = Integer.parseInt(temp[1]);
g[x].add(y);
g[y].add(x);
}
//g[x]代表当前点 g[x].get(i)代表所连的线
Queue<Integer> queue = new ArrayDeque<>();
for(int i=1;i<=n;i++){
if(strings[i-1].equals("R")){
queue.add(i);
visited[i]=1;
}
}
while(!queue.isEmpty()){
int temp=queue.remove();
for(int i=0;i<g[temp].size();i++){
if(visited[g[temp].get(i)]==0){
visited[g[temp].get(i)]=1;
dis[g[temp].get(i)]=dis[temp]+1;
queue.add(g[temp].get(i));
}
}
}
for(int i=1;i<=n;i++){
if(visited[i]==0)System.out.print("-1 ");
else System.out.print(dis[i]+" ");
}
}
}
对照上一章的案例:小红点点点结合理解。 分别使用的dfs和bfs。
本题思想:先将红色的所有点都入队列,然后bfs。
这是一种逆向思维:不是所谓的从编号开始,并且所有走过的都不能在走了。
3.小红玩数组
难度⭐⭐⭐⭐
知识点:双端队列
用一个双端队列来模拟过程,用一个变量来标记双端队列是否翻转过。


示例1:
输入
6 4
1 5 4 6 2 8
5
21323
输出
4 6 2 1 5 8
import java.io.*;
import java.util.*;
public class Main{
static Deque<Integer> workQueue;
public static void main(String[] args)throws IOException{
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
PrintWriter pw=new PrintWriter(System.out);
String[] firstLine=br.readLine().split(" ");
int total=Integer.parseInt(firstLine[0]);
int size=Integer.parseInt(firstLine[1]);
int[] arr=new int[total];
String[] secondLine=br.readLine().split(" ");
for(int i=0;i<total;i++){
arr[i]=Integer.parseInt(secondLine[i]);
}
int L=0;
int R=size-1;
workQueue=new LinkedList<>();
for(int i=0;i<size;i++){
workQueue.offerLast(arr[i]);
}
int times=Integer.parseInt(br.readLine());
String tries=br.readLine();
int is=0;//0代表没有翻转!
for(int i=0;i<times;i++){
if(tries.charAt(i)=='1'){
if(R==arr.length-1)
continue;
R++;
if(is==0){
workQueue.offerLast(arr[R]);
int tmp=workQueue.pollFirst();
arr[L]=tmp;
}else{
workQueue.offerFirst(arr[R]);
int tmp=workQueue.pollLast();
arr[L]=tmp;
}
L++;
}else if(tries.charAt(i)=='2'){
if(L==0)
continue;
L--;
if(is==0){
workQueue.offerFirst(arr[L]);
arr[R]=workQueue.pollLast();
}else{
workQueue.offerLast(arr[L]);
arr[R]=workQueue.pollFirst();
}
R--;
}else{
is=1-is;
}
}
for(int i=0;i<L;i++){
pw.print(arr[i]+" ");
}
if(is==0){
while(!workQueue.isEmpty()) {
pw.print(workQueue.pollFirst() + " ");
}
}else{
while(!workQueue.isEmpty()) {
pw.print(workQueue.pollLast() + " ");
}
}
for(int i=R+1;i<arr.length;i++){
pw.print(arr[i]+" ");
}
pw.flush();
}
}
加载全部内容