Python绘制数学函数图像

时间:2022-05-28 manchan4869 人气:0

前言

最近开始学习数学了，有一些题目的函数图像非常有特点，有一些函数图像手绘比较麻烦，那么有没有什么办法做出又标准又好看的数学函数图像呢？

答案是有很多的，有很多不错的软件都能画出函数图像，但是，我想到了Python的数据可视化。Python在近些年非常火热，在数据分析以及深度学习等方面得到广泛地运用，其丰富的库使其功能愈加强大。

这里我们使用Python的NumPy库以及Matplotlib库进行绘图。

NumPy与Matplotlib

NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。

Matplotlib 是 Python 的绘图库。它可与 NumPy 一起使用，提供了一种有效的 MatLab 开源替代方案。

函数绘图

所需库函数语法

import 语句

想使用 Python 源文件，只需在另一个源文件里执行 import 语句，语法如下：

import module1[, module2[,... moduleN]

from … import 语句

Python 的 from 语句让你从模块中导入一个指定的部分到当前命名空间中，语法如下：

from modname import name1[, name2[, ... nameN]]

numpy.arange

numpy 包中的使用 arange 函数创建数值范围并返回 ndarray 对象，函数格式如下：

numpy.arange(start, stop, step, dtype)

根据 start 与 stop 指定的范围以及 step 设定的步长，生成一个 ndarray。

参数说明：

参数	描述
start	起始值，默认为0
stop	终止值（不包含）
step	步长，默认为1
dtype	返回ndarray的数据类型，如果没有提供，则会使用输入数据的类型。

numpy.linspace

numpy.linspace 函数用于创建一个一维数组，数组是一个等差数列构成的，格式如下：

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

参数说明：

参数	描述
start	序列的起始值
stop	序列的终止值，如果endpoint为true，该值包含于数列中
num	要生成的等步长的样本数量，默认为50
endpoint	该值为 true 时，数列中包含stop值，反之不包含，默认是True。
retstep	如果为 True 时，生成的数组中会显示间距，反之不显示。
dtype	ndarray 的数据类型

导入所需模块

import numpy as np
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号

一元一次函数

# 一元一次函数图像
x = np.arange(-10, 10, 0.1)#生成等差数组
y = 2 * x
plt.xlabel('x')
plt.ylabel('y')
plt.title("一元一次函数")
plt.plot(x, y)
plt.show()

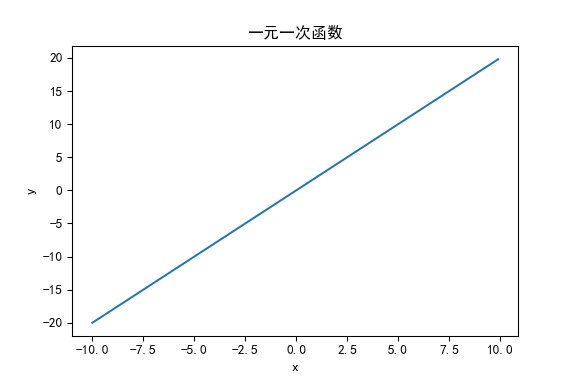
一元二次函数

# 一元二次函数图像
x = np.arange(-10, 10, 0.1)
y = x * x
plt.xlabel('x')
plt.ylabel('y')
plt.title("一元二次函数")
plt.plot(x, y)
plt.show()

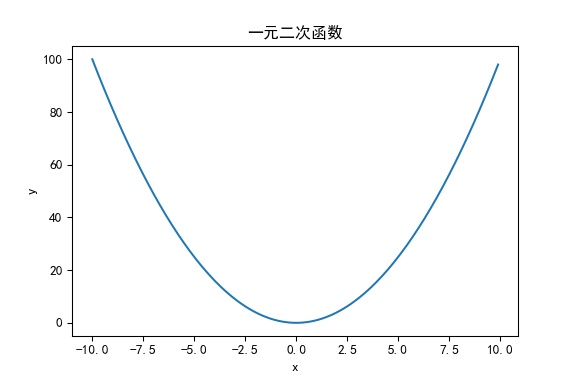
指数函数

# 指数函数
x = np.arange(-10, 10, 0.1)
y = np.power(2, x)
plt.xlabel('x')
plt.ylabel('y')
plt.title("指数函数")
plt.plot(x, y)
plt.show()

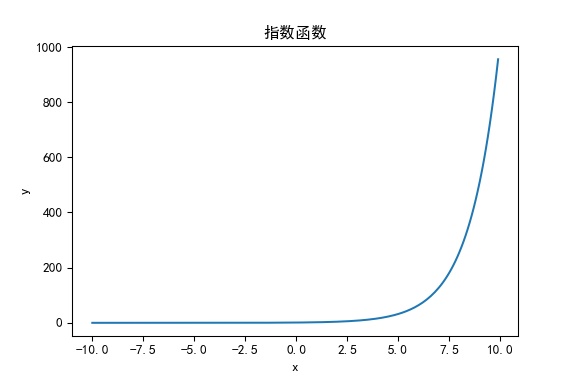
正弦函数

x = np.arange(-3 * np.pi, 3 * np.pi, 0.1)
y = np.sin(x)
plt.xlabel('x')
plt.ylabel('y')
plt.title("正弦函数")
plt.plot(x, y)
plt.show()

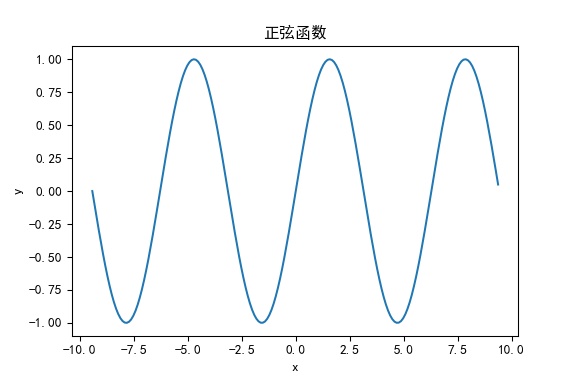
余弦函数

x = np.arange(-3 * np.pi, 3 * np.pi, 0.1)
y = np.cos(x)
plt.xlabel('x')
plt.ylabel('y')
plt.title("余弦函数")
plt.plot(x, y)
plt.show()

高级玩法

from pylab import *
import numpy
figure(figsize=(12,8), dpi=72)

# 创建一个新的 1 * 1 的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
subplot(1,1,1)

X = np.linspace(-np.pi*2, np.pi*2, 2048,endpoint=True)
C,S = np.cos(X), np.sin(X)

# 绘制余弦曲线，使用蓝色的、连续的、宽度为 1 （像素）的线条
plot(X, C,linewidth=1.5, linestyle="-",label="正弦")

# 绘制正弦曲线，使用绿色的、连续的、宽度为 1 （像素）的线条
plot(X, S,linewidth=1.5, linestyle="-",label="余弦")
legend(loc='upper left')
# 设置横轴的上下限
xlim(-4.5,4.5)

# 设置横轴记号
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])

# 设置纵轴的上下限
ylim(-1.5,1.5)

# 设置纵轴记号
yticks(np.linspace(-1,1,5,endpoint=True))
ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

# savefig("sincosin.png",dpi=72) #以72dpi保存图像

# 在屏幕上显示
show()

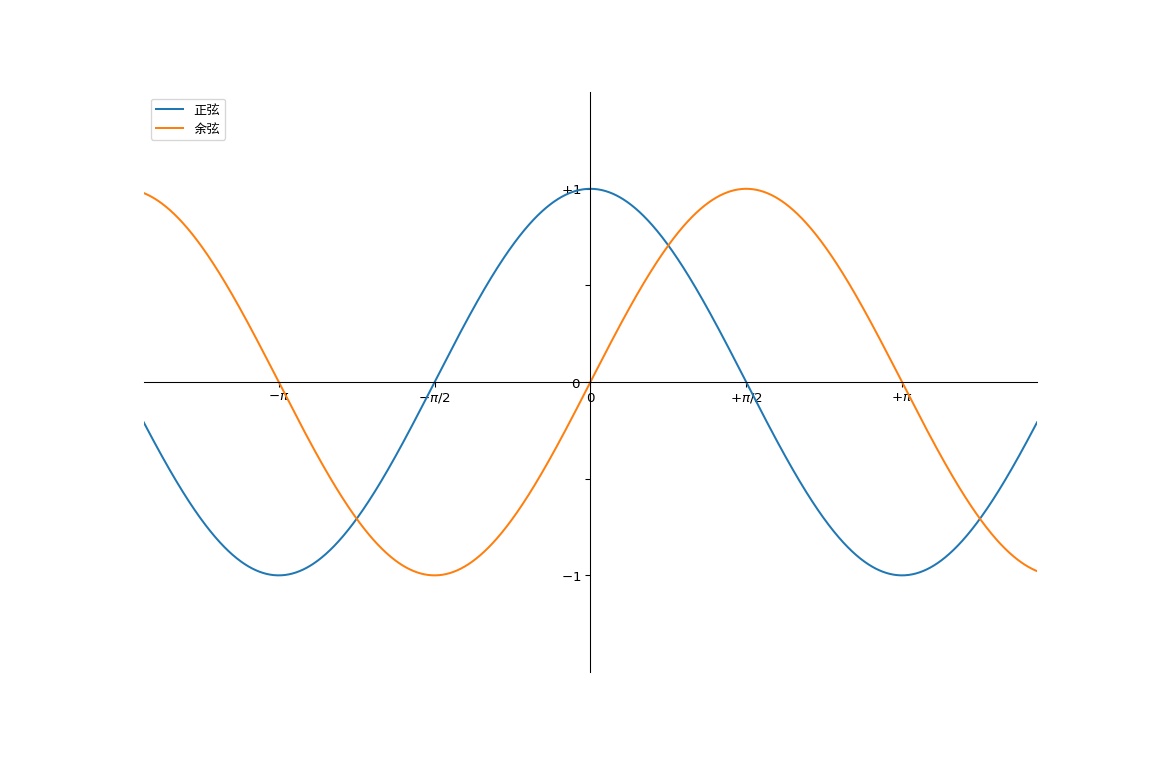
fig = plt.figure(figsize=(12,8), dpi=72)
x = np.arange(-10, 10, 0.01)
arsinh = np.log(x+np.sqrt(x**2+1))
sinh=0.5*(e**x-e**(-x))
cosh=0.5*(e**x+e**(-x))

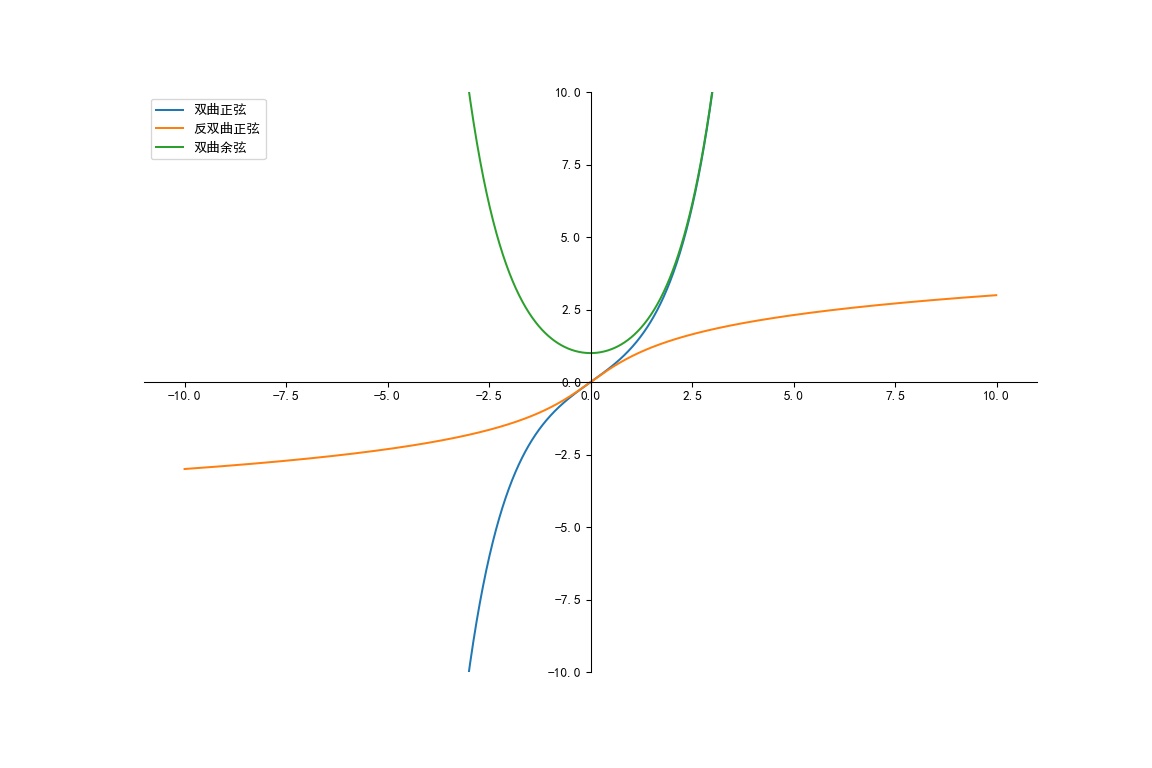
plt.plot(x, sinh,label="双曲正弦")
plt.plot(x, arsinh,label="反双曲正弦")
plt.plot(x, cosh,label="双曲余弦")

plt.legend(loc='upper left')

ylim(-10,10)

ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

plt.show()

总结

加载全部内容