C语言魔方阵
编程小程 人气:0魔方阵:
把1到n*n排成n行n列方阵,使方阵中的每一行、每一列以及对角线上的数之和都相同,即为n阶魔方阵。
根据魔方阵的规律,我将它分为三种情况。
1.奇数阶魔方阵
规律:第一个数放在第一行的中间,下一个数放在上一个数的上一行下一列,若该位置已经有了数字即放在上个数的下面一行的相同列
用C语言编程如下:
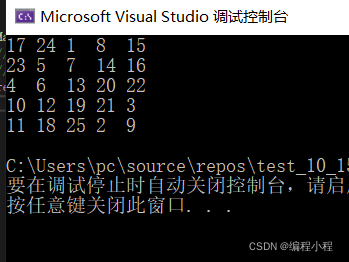
示例:n=5;
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
void Magic1()
{
#define ROW 5
#define COL ROW
assert(ROW % 2 != 0); //判断n是否为奇数
int arr[ROW][COL] = { 0 }; //定义二维数组
int currow = 0;
int curcol = COL / 2;
arr[currow][curcol] = 1;
for (int i = 2; i <= ROW * COL; i++)
{
if (arr[(currow - 1 + ROW) % ROW][(curcol + 1) % COL] == 0) //按照规律赋值
{
currow = (currow - 1 + ROW) % ROW;
curcol = (curcol + 1) % COL;
}
else
{
currow = (currow + 1) % ROW;
}
arr[currow][curcol] = i;
}
for (int i = 0; i < ROW; i++) //打印魔方阵
{
for (int j = 0; j < COL; j++)
{
printf("%-3d", arr[i][j]);
}
printf("\n");
}
}
int main()
{
Magic1();
return 0;
}
结果:
2.偶数阶魔方阵 (n=4K)
规律:按数字从小到大,即1,2,3……n顺序对魔方阵从左到右,从上到下进行填充;
将魔方阵分成若干个4×4子方阵(如:8阶魔方阵可分成四个4×4子方阵),将子方阵对角线上的元素取出;将取出的元素按从大到小的顺序依次填充到n×n方阵的空缺处。
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//偶数魔方阵 4K
void Magic2()
{
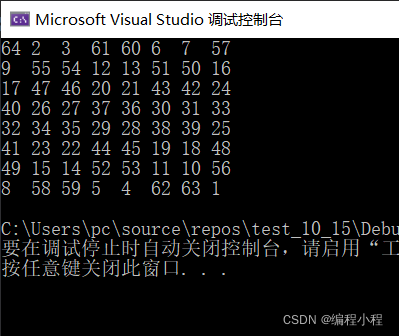
#define ROW 8
#define COL ROW
int tmp = 1;
int arr[ROW][COL] = { 0 }; //定义二维矩阵
for (int i = 0; i < ROW; i++)
{
for (int j = 0; j < COL; j++)
{
arr[i][j] = tmp++;
}
}
int row1 = 1;
int col1 = 1;
int row2 = 1;
int col2 = 1;
for (int i = 0; i < (ROW / 4) ; i++)
{
for (int j = 0; j < (COL / 4); j++)
{
row1 = 4 * i;
col1 = 4 * j;
row2 = 4 * i;
col2 = 4 * j + 3;
for (int k = 0; k < 4; k++)
{
arr[row1][col1] = (ROW * COL + 1) - arr[row1][col1];
arr[row2][col2] = (ROW * COL + 1) - arr[row2][col2];
row1++;
col1++;
row2++;
col2--;
}
}
}
for (int i = 0; i < ROW; i++)
{
for (int j = 0; j < COL; j++)
{
printf("%-3d", arr[i][j]);
}
printf("\n");
}
}
int main()
{
Magic2();
return 0;
}
结果:
3.偶数阶魔方阵 (n=4K+2)
规律:
3.1.填充规则
将魔方分成A、B、C、D四个k阶奇方阵, 利用奇数魔方阵填充方法依次将A、D、B、C填充 。
3.2.交换规则 上下标记的数字进行交换
1.右半边大于k+2的列(从1开始)
2.左半边,上下两个块最中心的点进行交换
3.左半边小于中心列的列(除了上下半边最中心的行的第一列的那个值不用交换)(从1开始)
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
void Magic3()
{
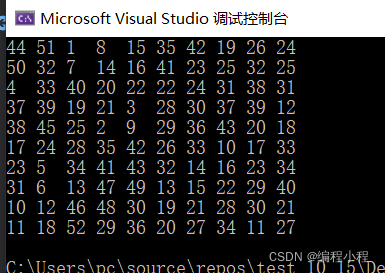
#define ROW 10
#define COL ROW
assert(ROW % 2 == 0 && ROW % 4 != 0);
int arr[ROW][COL] = { 0 };
//左上角
int currow = 0;
int curcol = ROW/4;
arr[currow][curcol] = 1;
int tmp = 0;
for (int i = 2; i <= ROW * COL/ 4; i++)
{
if (arr[(currow - 1 + ROW / 2) % (ROW / 2)][(curcol + 1) % (COL / 2)] == 0) //判断上一行下一列是否被赋值
{
currow = (currow - 1 + ROW / 2) % (ROW / 2);
curcol = (curcol + 1) % (COL / 2);
}
else
{
currow = (currow + 1) % (ROW / 2);
}
arr[currow][curcol] = i;
}
//右下角
currow = ROW / 2;
for (int i = 0; i < ROW / 2; i++, currow++)
{
curcol = COL / 2;
for (int j = 0; j < COL / 2; j++, curcol++)
{
arr[currow][curcol] = arr[i][j] + 9;
}
}
//右上角
currow = 0;
for (int i = ROW/2; i < ROW ; i++, currow++)
{
curcol = COL / 2;
for (int j = COL/2; j < COL; j++, curcol++)
{
arr[currow][curcol] = arr[i][j] + 9;
}
}
//左下角
currow = ROW / 2;
for (int i = 0; i < ROW/2; i++, currow++)
{
curcol = 0;
for (int j = COL/2; j < COL; j++, curcol++)
{
arr[currow][curcol] = arr[i][j] + 9;
}
}
//替换规则1:右半边 大于k+2的列 进行上下交换
for (int i = 0; i < ROW / 2; i++)
{
for (int j = ROW / 2 + ROW / 4 + 2; j < COL; j++)
{
tmp = arr[i][j];
arr[i][j] = arr[i + ROW / 2][j];
arr[i + ROW / 2][j] = tmp;
}
}
//替换规则2:交换左半边,两个中心节点
currow = ROW / 4;
curcol = COL / 4;
tmp = arr[currow][curcol];
arr[currow][curcol] = arr[currow + ROW / 2][curcol];
arr[currow + ROW / 2][curcol] = tmp;
//替换规则3:左半边,除(K+1,1)这个点外,小于k+1的列 上下交换
for (int j = 0; j < ROW / 4; j++) //表示交换的列
{
for (int i = 0; i < ROW / 2; i++) //表示交换的行
{
if (i == ROW / 4 && j == 0)
{
continue;
}
else
{
tmp = arr[i][j];
arr[i][j] = arr[i + ROW / 2][j];
arr[i + ROW / 2][j] = tmp;
}
}
}
//打印
for (int i = 0; i < ROW; i++)
{
for (int j = 0; j < COL; j++)
{
printf("%-3d", arr[i][j]);
}
printf("\n");
}
}
int main()
{
Magic3();
return 0;
}
结果:
加载全部内容