C语言中的rand()和rand_r()

时间:2022-05-23 高阶近似人气:0

背景

最近在学《并行程序设计导论》这门课，在做使用Pthreads并行化蒙特卡洛法估计 π \pi π的实验时遇到了一个问题，使用多线程反而要比单线程要慢很多，输出如下所示

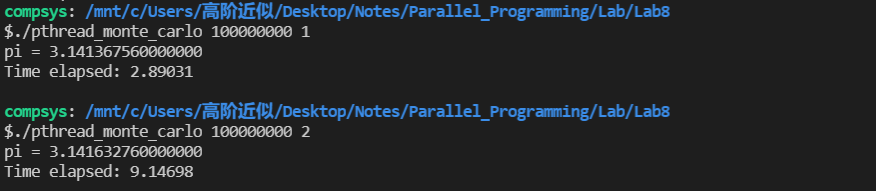
请添加图片描述

可以看到，使用一个线程时程序运行只需要2.89031秒，但是使用两个线程时运行时间竟然达到了9.14698秒。

最终发现了问题所在：每个线程在执行下面的函数时，生成随机数使用了rand()函数，就是这个函数的使用才导致多线程运行时所需要的时间反而更长

long long total_times_in_cycle;
long long local_number_toss;
pthread_mutex_t times_in_cycle_mutex = PTHREAD_MUTEX_INITIALIZER;
void* do_Monte_Carlo_simulation(void* my_rank){
	double offset = RAND_MAX / (double)2;
    long long times_in_cycle = 0;
    long long i;
    for(i = 0; i < local_number_toss; ++i){
        double x = rand() / offset - 1;
        double y = rand() / offset - 1;
        if(x*x + y*y < 1){
            times_in_cycle++;
        }
    }
    pthread_mutex_lock(&times_in_cycle_mutex);
    total_times_in_cycle += times_in_cycle;
    pthread_mutex_unlock(&times_in_cycle_mutex);
}

rand()和rand_r()的区别

权威的解释请参考Linux的官方文档
这里主要说说我个人的理解。

rand()

对于rand():
srand()和rand()配套一起使用，可以认为是进程只生成了一个随机数生成器，所有的线程共用这个随机数生成器。每调用一次rand()，rand()都会去修改这个随机数生成器的一些参数，比如说当前种子的值。对于单线程，这样是没有问题的，但是对于多线程而言，这显然会导致临界段问题，为了解决该问题，可能会使用互斥量等方法，下面假设多个线程同时使用rand()的时候使用互斥量来解决该临界段问题。如果rand()调用的次数不多，多线程也问题不大，但是对于上述蒙特卡洛法估计 π \pi π的程序，需要调用很多次rand()，这可能会导致每个线程频繁地对临界段进行上锁和解锁，而临界段被上锁后，其他线程无法完成rand()的调用从而被阻塞，这样会导致效率十分低下，因此会出现使用多线程反而程序运行更慢的问题。

srand()和rand()配套一起使用，可以认为是进程只生成了一个随机数生成器，所有的线程共用这个随机数生成器这点可以用下面的程序进行验证，该程序从命令行获取要生成随机数的数量以及线程的数量，每个线程负责生成随机数的数量/线程的数量个随机数，随机数种子设为0.

#include<stdio.h>
#include<pthread.h>
#include<stdlib.h>

int generate_rand_count;
int thread_count;

// 被线程执行的函数
void* thread_func(void* my_rank){
    int i;
    int local_rand_count = generate_rand_count / thread_count;
    for(i = 0; i < local_rand_count; ++i){
        printf("%d ", rand());
    }
}

int main(int argc, char* argv[]){
    pthread_t* all_threads_id;

    // 从命令行获取要生成的随机数的数量以及这些随机数由多少个线程来生成
    generate_rand_count = strtol(argv[1], NULL, 10);
    thread_count = strtol(argv[2], NULL, 10);
    all_threads_id = malloc(sizeof(pthread_t) * thread_count);

    // 设置随机数种子
    srand(0);

    // 创建线程
    int i;
    for(i = 0; i < thread_count; ++i){
        pthread_create(&all_threads_id[i], NULL, thread_func, (void*) i);
    }

    for(i = 0; i < thread_count; ++i){
        pthread_join(all_threads_id[i], NULL);
    }
    
    printf("\n");
    free(all_threads_id);
    return 0;
}

执行结果如下所示

请添加图片描述

可以看到，无论使用一个线程生成10个随机数，还是说使用两个线程来生成10个随机数，它们生成的这10个随机数是一样的，这也就验证了所有的线程共用一个随机数生成器的观点

rand_r()

rand_r()的声明如下所示

int rand_r(unsigned int *seedp);

每次使用rand_r()的时候需要传给该函数一个随机数种子的指针，为了解决蒙特卡洛方法估计 π \pi π中出现的问题，使用如下的代码：

long long total_times_in_cycle;
long long local_number_toss;
pthread_mutex_t times_in_cycle_mutex = PTHREAD_MUTEX_INITIALIZER;
void* do_Monte_Carlo_simulation(void* my_rank){
	unsigned int local_seed = time(NULL);
	double offset = RAND_MAX / (double)2;
    long long times_in_cycle = 0;
    long long i;
    for(i = 0; i < local_number_toss; ++i){
        double x = rand_r(&local_seed) / offset - 1;
        double y = rand_r(&local_seed) / offset - 1;
        if(x*x + y*y < 1){
            times_in_cycle++;
        }
    }
    pthread_mutex_lock(&times_in_cycle_mutex);
    total_times_in_cycle += times_in_cycle;
    pthread_mutex_unlock(&times_in_cycle_mutex);
}

每个线程执行函数do_Monte_Carlo_simulation()。

使用上面的代码后，相当于每个线程生成了它自己独有的随机数生成器，这样就不会有临界段问题，从而解决了多线程运行时所需要的时间反而更长这个问题，下面为更改后程序的输出：

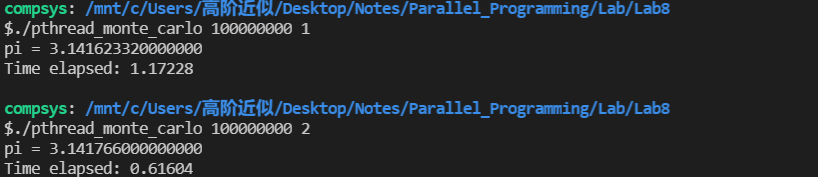
请添加图片描述

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注的更多内容!

加载全部内容