C++转置矩阵循环
Alkaid#3529 人气:0前言
矩阵的转置主要考查我们对循环的使用,通过简单的循环结构,我们可以很方便的完成矩阵的转置。
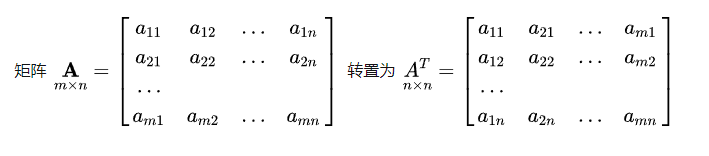
一、思路分析
转置矩阵与原矩阵的区别在于行列交换,我们可以构建一个二维数组完成对原矩阵的存储,我们只需将每个元素与其行列相反的位置处的元素进行交换,就可完成对矩阵的转置。
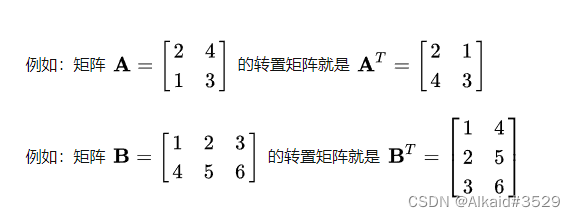
二、代码实现
1.转置矩阵函数
我们首先编写一个函数,完成对矩阵的转置。
代码如下(示例):
/* Alkaid#3529 */
// 转职矩阵函数,按照指定的矩阵大小将矩阵转置
void transpose_matrix(int matrix[10][10], int a);
// 函数实现
void transpose_matrix(int matrix[10][10], int a) // int matrix[10][10] 为存储矩阵的数组,int a 为所需转置矩阵的大小
{
int mid = 0; // 中间量,辅助值的传递
for (int i = 0; i < a; i++) // 从行开始,逐行检索
{
for (int j = i + 1; j < a; j++) // 对该行每一列的元素检索
{
// 将对应位置的两个元素交换位置
mid = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = mid;
}
}
return;
}
2.调用函数实现转置矩阵
我们在主函数中只需调用已经写好的函数,对转置前后的矩阵分别输出即可。
代码如下(示例):
/* Alkaid#3529 */
#include<iostream>
using namespace std;
// 转职矩阵函数,按照指定的矩阵大小将矩阵转置
void transpose_matrix(int matrix[10][10], int a);
int main()
{
int matrix[10][10];
int size = 0;
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 10; j++)
{
matrix[i][j] = (i * i + j * i + j ^ i) % 10;
}
}
// 读入要求的矩阵大小,方便起见,使用矩阵的默认值,默认为方阵
cout << "请输入矩阵的尺寸 (方便起见,矩阵大小设在10以内) :\n";
cout << "size = ";
cin >> size;
cout << "\n原矩阵为:\n";
// 输出原矩阵
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
cout << matrix[i][j] << " ";
}
cout << endl;
}
transpose_matrix(matrix, size);
cout << "\n转置后的矩阵为:\n";
// 输出转置后的矩阵
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
cout << matrix[i][j] << " ";
}
cout << endl;
}
return 0;
}
void transpose_matrix(int matrix[10][10], int a)
// int matrix[10][10] 为存储矩阵的数组,int a 为所需转置矩阵的大小
{
int mid = 0; // 中间量,辅助值的传递
for (int i = 0; i < a; i++) // 从行开始,逐行检索
{
for (int j = i + 1; j < a; j++) // 对该行每一列的元素检索
{
// 将对应位置的两个元素交换位置
mid = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = mid;
}
}
return;
}
运行程序,看看效果如何。
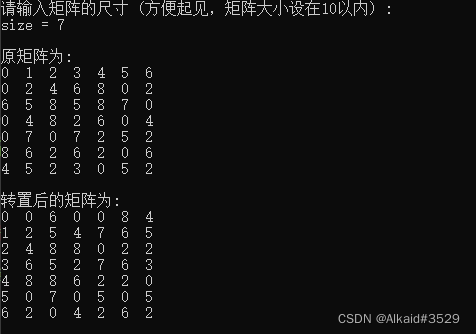
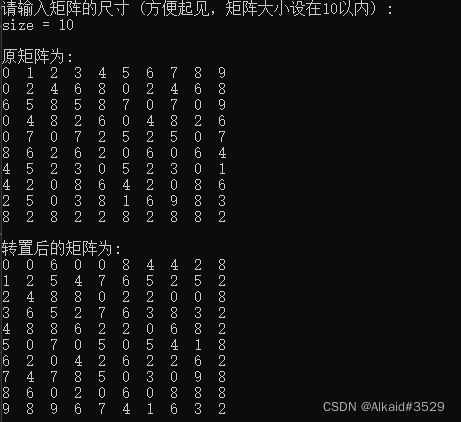
正常运行,且功能完整,可以放心复制黏贴使用。
总结
矩阵转置,除了本文介绍的方法外,还可以利用三元组的形式完成对稀疏矩阵的转置,感兴趣的话不妨点个关注,会在后续的数据和结构与算法专栏进行详细讲解哦!
加载全部内容