python验证多组数据之间有无显著差异
fff2zrx 人气:0一、方差分析
1.单因素方差分析

通过箱线图可以人肉看出10组的订单量看起来差不多,为了更科学比较10组的订单量有无显著差异,我们可以利用方差分析
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols('orders~C(label)',data=need_data).fit()
anova_table = anova_lm(model, typ = 2)
print(anova_table)
结果显示,p值为0.62大于0.05,不能拒绝原假设,所以这10组的订单量分布没有显著差异。
二、卡方检验
如果是比较多组之间的非连续值指标是否存在差异呢?
如检查上面10组的男女比例是否存在显著差异
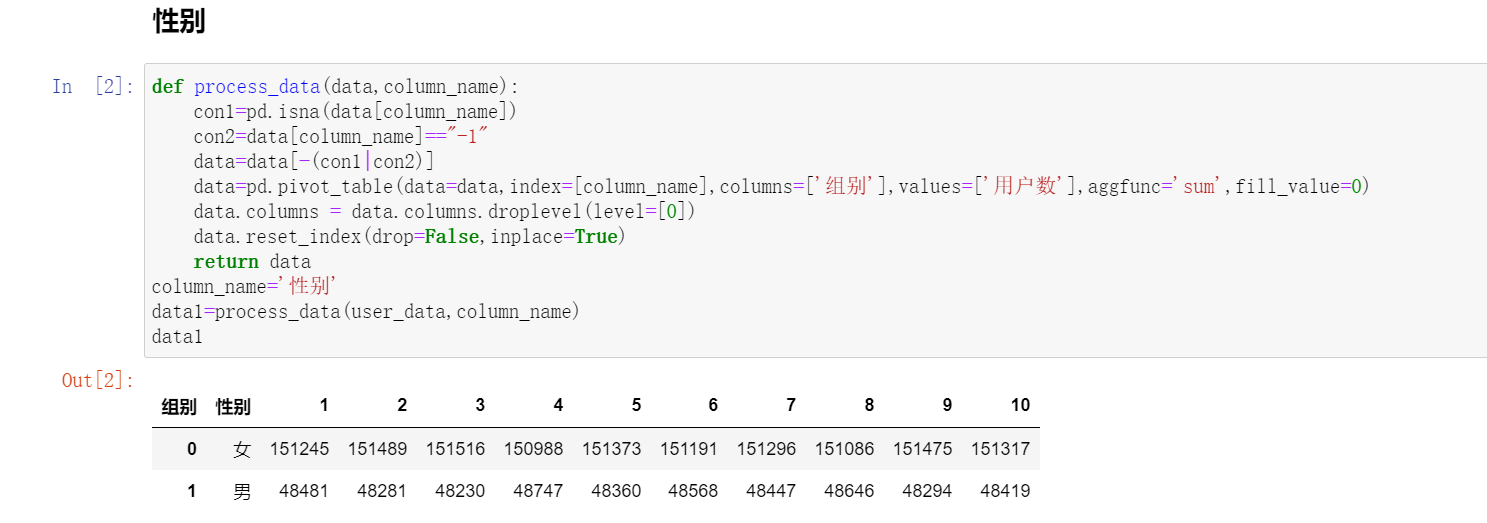
计算各组观察频数:
data2=data1.melt(id_vars=['性别'],value_name='观察频数') data2.head()

计算总体的男女比例:
rate=(data2.groupby(['性别'])['观察频数'].sum()/data2.groupby(['性别'])['观察频数'].sum().sum()).reset_index() rate.columns=['性别','rate'] rate

计算各组用户总数:
group_sum=data2.groupby(['组别'])['观察频数'].sum().reset_index() group_sum.columns=['组别','组内用户数'] group_sum

计算卡方值:
import math data3=pd.merge(data2,group_sum,on=['组别'],how='left') data3=pd.merge(data3,rate,on=['性别'],how='left') data3['期望频数']=data3['组内用户数']*data3['rate'] data3['卡方值']=data3.apply(lambda x: math.pow((x.期望频数-x.观察频数),2)/x.期望频数,axis=1) data3.head()
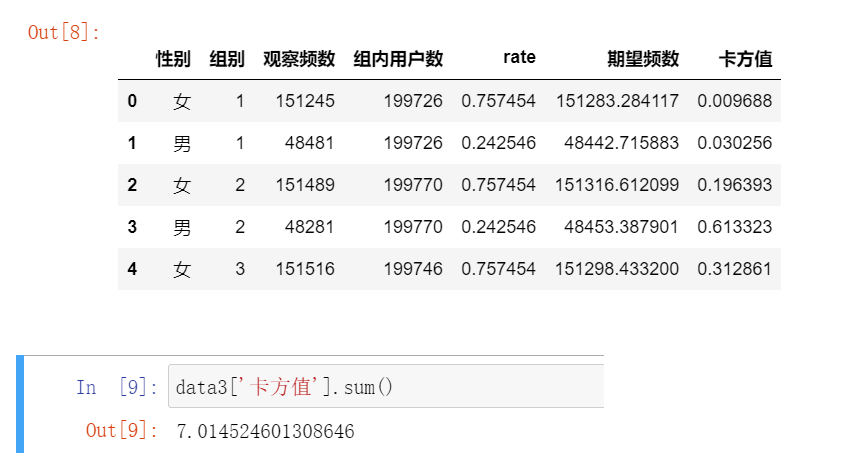
本案例的自由度为(10-1)*(2-1)=9,选取显著性水平为0.05,查卡方分布表得临界值为18.31
因为7.01<18.31,所以不能拒绝原假设,即各组的性别分布不存在显著性差异。
加载全部内容