C语言打印杨辉三角
小辉_Super 人气:0题目描述
打印杨辉三角(前N行)
问题分析
杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。
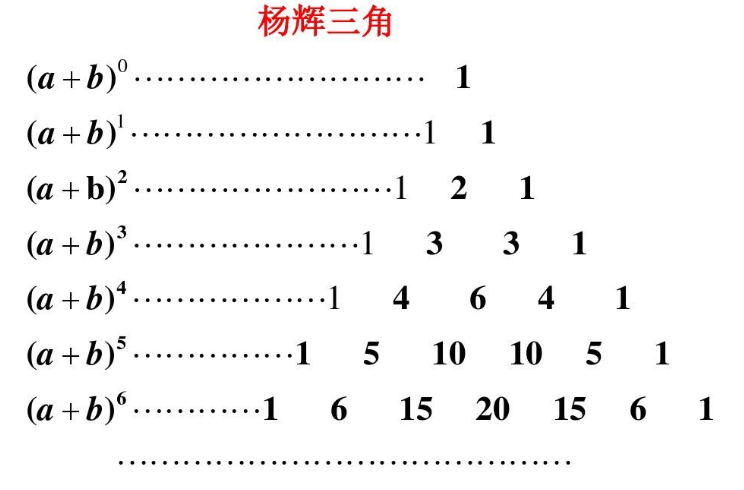
杨辉三角的部分规律:
- 每个数等于它上方两数之和。
- 每行数字左右对称,由1开始逐渐变大。
- 第n行的数字有n项。
- 第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
根据前三个规律,我们可以使用数组法获取杨辉三角;根据后两个规律,我们可以使用公式法求出每行每列的数字。
数组法思路:先根据设定的行数定义一个二维数组,然后使用一个双层循环,外层循环的因数为杨辉三角的行数,内层循环用来将杨辉三角每行的数字存入数组。每行第一列和最后一列都是1,中间的数字等于它上方两数之和。
最后再通过两层循环将二维数组中的数字打印。
公式法思路:由于杨辉三角满足上面提到的第4点规律,所以我们可以直接定义一个函数求出杨辉三角第n行的m个数的值。
组合数公式
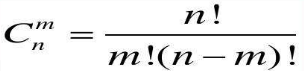
根据上面这个组合的公式,我们可以使用阶乘及相关计算,求出杨辉三角形的每个数,同时打印出来。
1. 使用数组法(打印直角三角)
打印直角形式的杨辉三角形,即打印二维数组时不加空格
代码
#include <stdio.h>
#define LINE_MAXIMUM 10 //行数
int main()
{
int i = 0, j = 0;
int array[LINE_MAXIMUM][LINE_MAXIMUM] = {0};
/* 填充二维数组 */
for(i = 0; i < LINE_MAXIMUM; i++) //行数
{
for(j = 0; j <= i; j++) //每行的列数(第n行的数字有n项)
{
if(j == 0 || j == i) //每行第一列和最后一列为1
array[i][j] = 1;
else //每个数等于它上方两数之和
array[i][j] = array[i - 1][j - 1]\
+ array[i - 1][j];
}
}
/* 打印杨辉三角(直角) */
for(i = 0; i < LINE_MAXIMUM; i++)
{
for(j = 0; j <= i; j++)
printf("%d ", array[i][j]);
printf("\n");
}
return 0;
}
运行结果
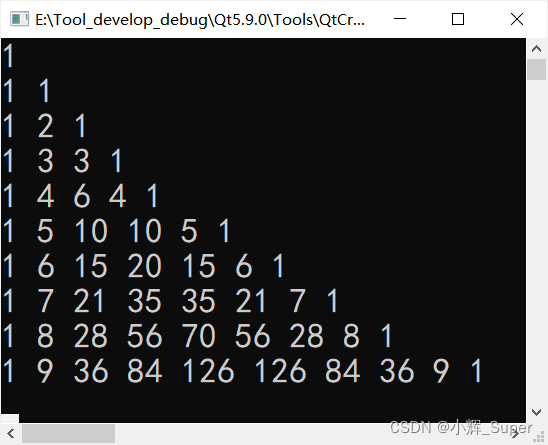
2. 使用数组法(打印等腰三角)
打印等腰形式的杨辉三角形,需要在每行前面加若干空格,空格的宽度需要根据数字的宽度调整,使三角形对称。
代码
#include <stdio.h>
#define LINE_MAXIMUM 10 //行数
int main()
{
int i = 0, j = 0;
int array[LINE_MAXIMUM][LINE_MAXIMUM] = {0};
int k = 0;
/* 填充二维数组 */
for(i = 0; i < LINE_MAXIMUM; i++) //行数
{
for(j = 0; j <= i; j++) //每行的列数(第n行的数字有n项)
{
if(j == 0 || j == i) //每行第一列和最后一列为1
array[i][j] = 1;
else //每个数等于它上方两数之和
array[i][j] = array[i - 1][j - 1]\
+ array[i - 1][j];
}
}
/* 打印杨辉三角(等腰) */
for(i = 0; i < LINE_MAXIMUM; i++)
{
//在数字前打印空格,最后一行空格数为0
for(k = 1; k < LINE_MAXIMUM - i; k++)
printf(" ");
for(j = 0; j <= i; j++)
printf("%3d ", array[i][j]);
printf("\n");
}
return 0;
}
运行结果
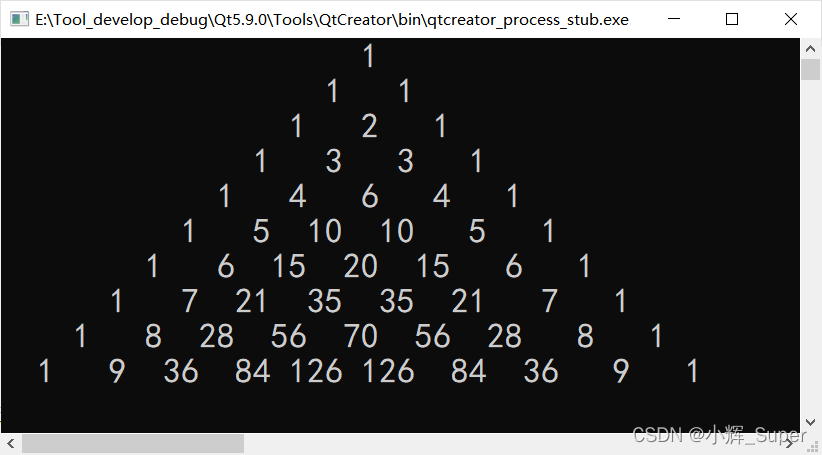
3. 使用公式法(打印等腰三角)
由于循环都是从 0 开始,所以核心函数的功能是获取杨辉三角第 m + 1 行,第 n + 1 个数的值(行数最小为1),即求C(m,n)。另外,由于公式中存在除法,所以行数列数及结果不能使用整型,需要用浮点型。
代码
#include<stdio.h>
#define LINE_MAXIMUM 10 //行数
/**
* @brief 获得阶乘结果(递归实现)
* @param num 输入的参数
* @return 返回num!(阶乘)
*/
float Get_Factorial(float num)
{
if(num >= 1)
return num * Get_Factorial(num - 1);
else //0! = 1
return 1;
}
//获取杨辉三角第 m + 1 行,第 n + 1 个数的值为 C(m,n)
float Get_Num(float m, float n)
{
return Get_Factorial(n) / Get_Factorial(m) / Get_Factorial(n - m) ;
}
int main()
{
float i = 0, j = 0, k = 0;
/* 打印杨辉三角(等腰) */
for(i = 0; i < LINE_MAXIMUM; i++)
{
//在数字前打印空格,最后一行空格数为0,第一行为空格数为LINE_MAXIMUM - 1
for(k = 1; k < LINE_MAXIMUM - i; k++)
printf(" ");
for(j = 0; j <= i; j++)
printf("%3.0f ", Get_Num(j, i));
printf("\n");
}
return 0;
}
运行结果

网上参考
这份代码看起来很简洁,使用的是公式法。
#include <stdio.h>
#include <stdlib.h>
int main()
{
int s = 1, h; // 数值和高度
int i, j; // 循环计数
scanf("%d", &h); // 输入层数
printf("1\n"); // 输出第一个 1
for (i = 2; i <= h; s = 1, i++) // 行数 i 从 2 到层高
{
printf("1 "); // 第一个 1
for (j = 1; j <= i - 2; j++) // 列位置 j 绕过第一个直接开始循环
printf("%d ", (s = (i - j) * s / j));
printf("1\n"); // 最后一个 1,换行
}
getchar(); // 暂停等待
return 0;
}
加载全部内容