Python 工业蒸汽数据分析
柚子味的羊 人气:0一、数据集
二、数据分析
1 数据导入
#%%导入基础包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
#%%读取数据
train_data_file = "D:\Python\ML\data\zhengqi_train.txt"
test_data_file = "D:\Python\ML\data\/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
#%%查看训练集特征变量信息
train_infor=train_data.describe()
test_infor=test_data.describe()
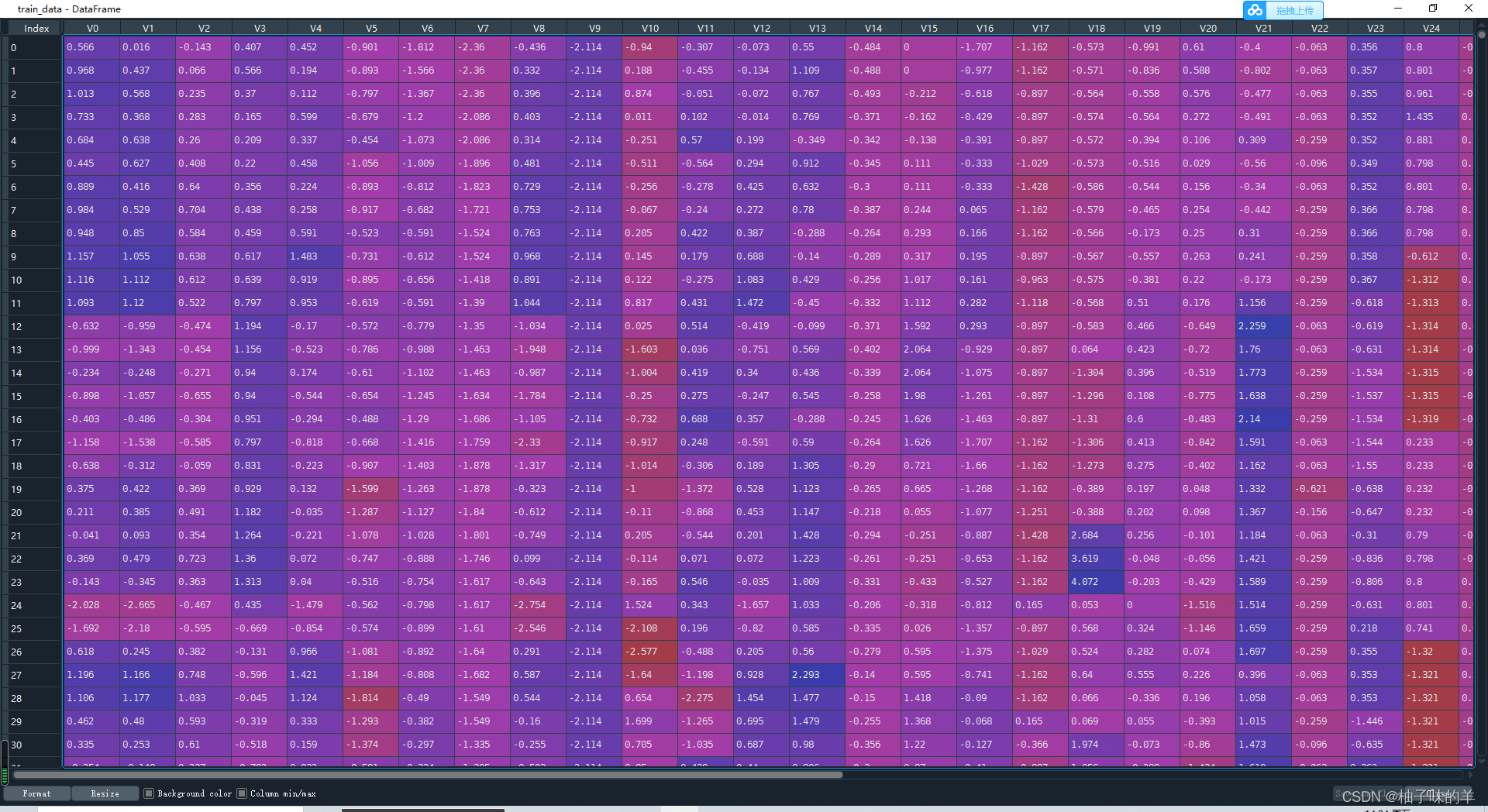

2 数据特征探索(数据可视化)
#%%可视化探索数据
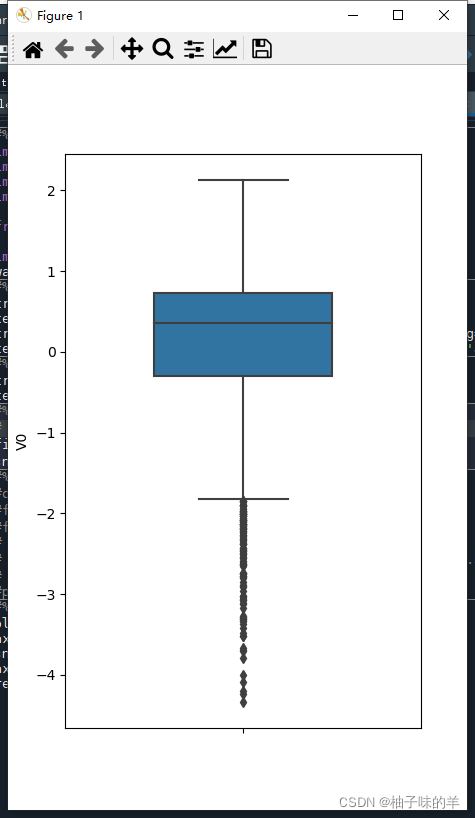
# 画v0箱式图
fig = plt.figure(figsize=(4, 6)) # 指定绘图对象宽度和高度
sns.boxplot(y=train_data['V0'],orient="v", width=0.5)
#%%可以将所有的特征都画出
'''
column = train_data.columns.tolist()[:39] # 列表头
fig = plt.figure(figsize=(20, 40)) # 指定绘图对象宽度和高度
for i in range(38):
plt.subplot(13, 3, i + 1) # 13行3列子图
sns.boxplot(train_data[column[i]], orient="v", width=0.5) # 箱式图
plt.ylabel(column[i], fontsize=8)
plt.show()
'''
#%%查看v0的数据分布直方图,绘制QQ图查看数据是否近似于正态分布
plt.figure(figsize=(10,5))
ax=plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax=plt.subplot(1,2,2)
res = stats.probplot(train_data['V0'], plot=plt)
#%%查看所有特征的数据分布情况
'''
train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4*train_cols,4*train_rows))
i=0
for col in train_data.columns:
i+=1
ax=plt.subplot(train_rows,train_cols,i)
sns.distplot(train_data[col],fit=stats.norm)
i+=1
ax=plt.subplot(train_rows,train_cols,i)
res = stats.probplot(train_data[col], plot=plt)
plt.show()
'''

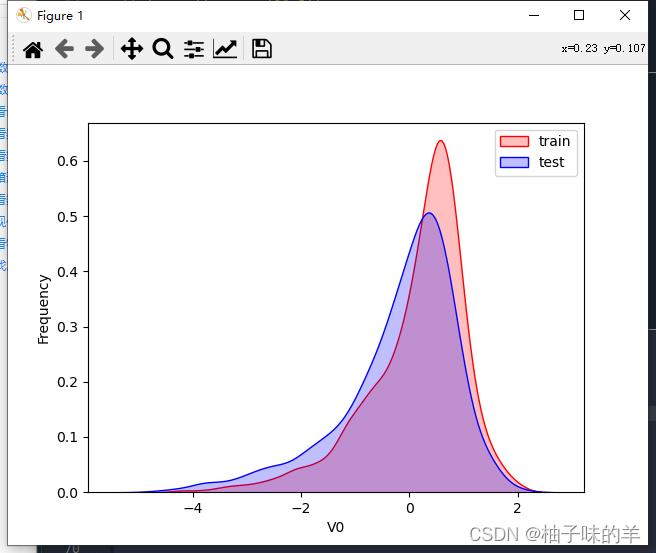
#%%对比统一特征训练集和测试集的分布情况,查看数据分布是否一致
ax = sns.kdeplot(train_data['V0'], color="Red", shade=True)
ax = sns.kdeplot(test_data['V0'], color="Blue", shade=True)
ax.set_xlabel('V0')
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])
#%%查看所有特征的训练集和测试集分布情况
'''
dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4*dist_cols,4*dist_rows))
i=1
for col in test_data.columns:
ax=plt.subplot(dist_rows,dist_cols,i)
ax = sns.kdeplot(train_data[col], color="Red", shade=True)
ax = sns.kdeplot(test_data[col], color="Blue", shade=True)
ax.set_xlabel(col)
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])
i+=1
plt.show()
'''
#%%查看v5,v9,v11,v22,v28的数据分布
drop_col = 6
drop_row = 1
plt.figure(figsize=(5*drop_col,5*drop_row))
i=1
for col in ["V5","V9","V11","V17","V22","V28"]:
ax =plt.subplot(drop_row,drop_col,i)
ax = sns.kdeplot(train_data[col], color="Red", shade=True)
ax = sns.kdeplot(test_data[col], color="Blue", shade=True)
ax.set_xlabel(col)
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])
i+=1
plt.show()
#%%删除这些特征
drop_columns=["V5","V9","V11","V17","V22","V28"]
train_data=train_data.drop(columns=drop_columns)
test_data=test_data.drop(columns=drop_columns)
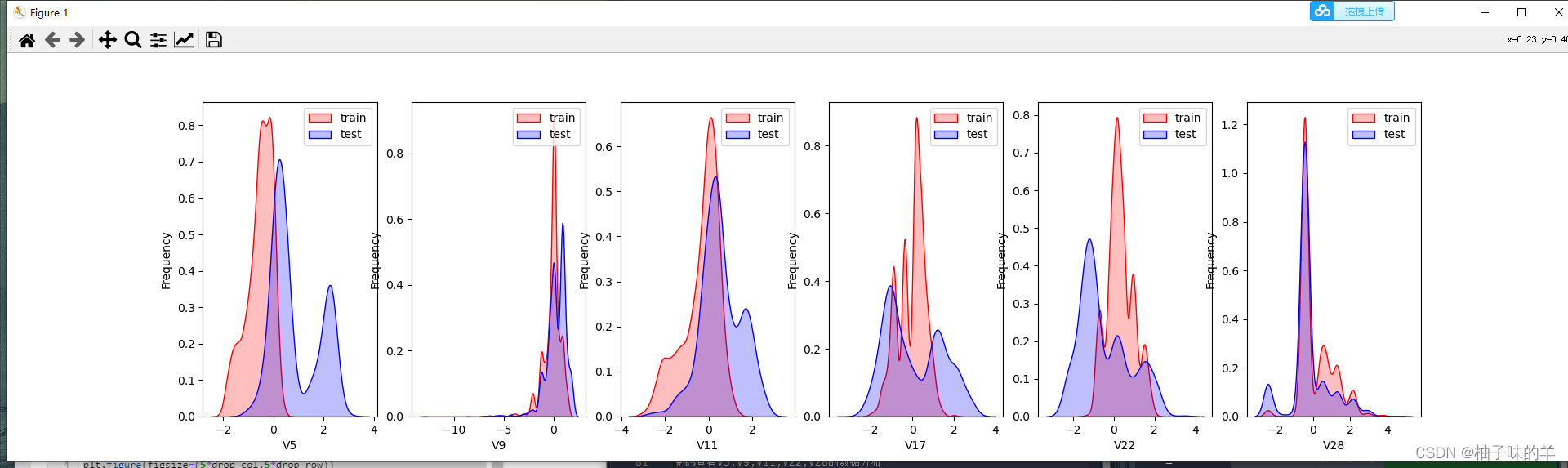
当训练数据和测试数据分布不一致的时候,会导致模型的泛化能力差,采用删除此类特征的方法

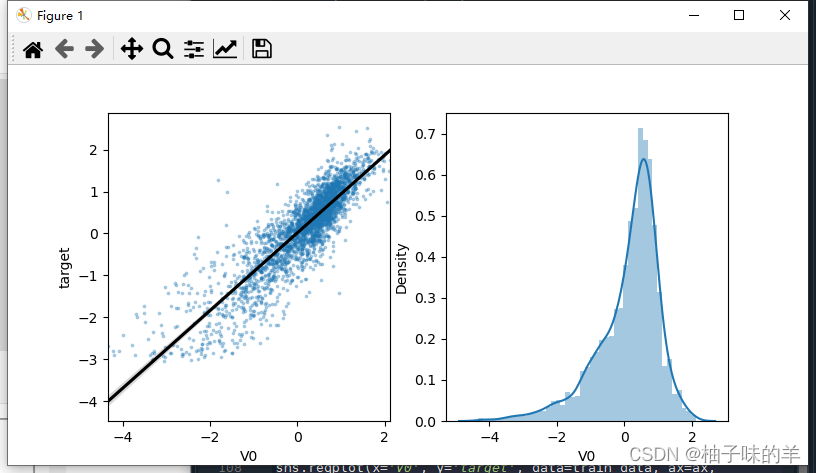
#%%可视化线性回归关系
fcols = 2
frows = 1
plt.figure(figsize=(8,4))
ax=plt.subplot(1,2,1)
sns.regplot(x='V0', y='target', data=train_data, ax=ax,
scatter_kws={'marker':'.','s':3,'alpha':0.3},
line_kws={'color':'k'});
plt.xlabel('V0')
plt.ylabel('target')
ax=plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')
plt.show()
#%%查看所有特征变量与target变量的线性回归关系
'''
fcols = 6
frows = len(test_data.columns)
plt.figure(figsize=(5*fcols,4*frows))
i=0
for col in test_data.columns:
i+=1
ax=plt.subplot(frows,fcols,i)
sns.regplot(x=col, y='target', data=train_data, ax=ax,
scatter_kws={'marker':'.','s':3,'alpha':0.3},
line_kws={'color':'k'});
plt.xlabel(col)
plt.ylabel('target')
i+=1
ax=plt.subplot(frows,fcols,i)
sns.distplot(train_data[col].dropna())
plt.xlabel(col)
'''
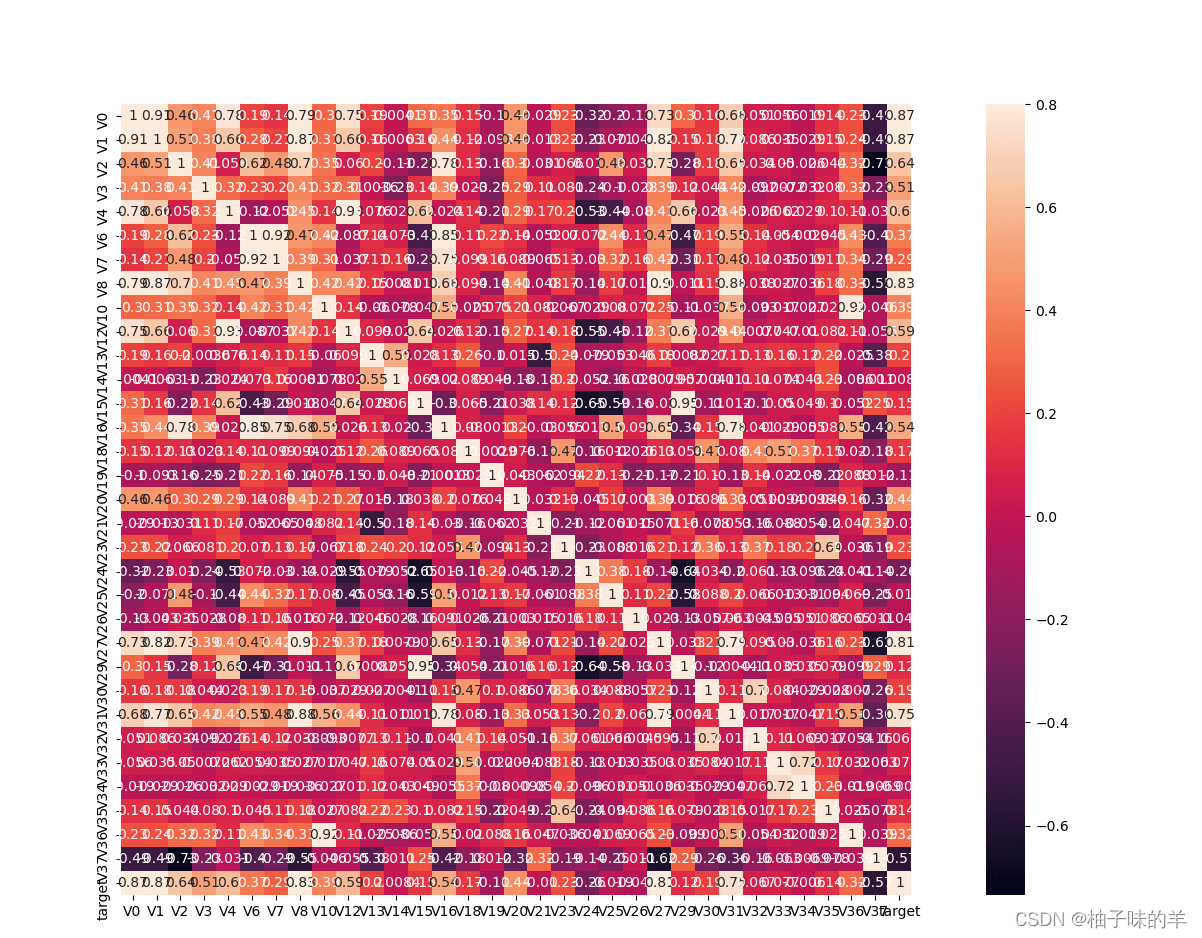
#%%查看特征变量的相关性 train_corr = train_data.corr() # 画出相关性热力图 ax = plt.subplots(figsize=(20, 16))#调整画布大小 ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True)#画热力图 annot=True 显示系数
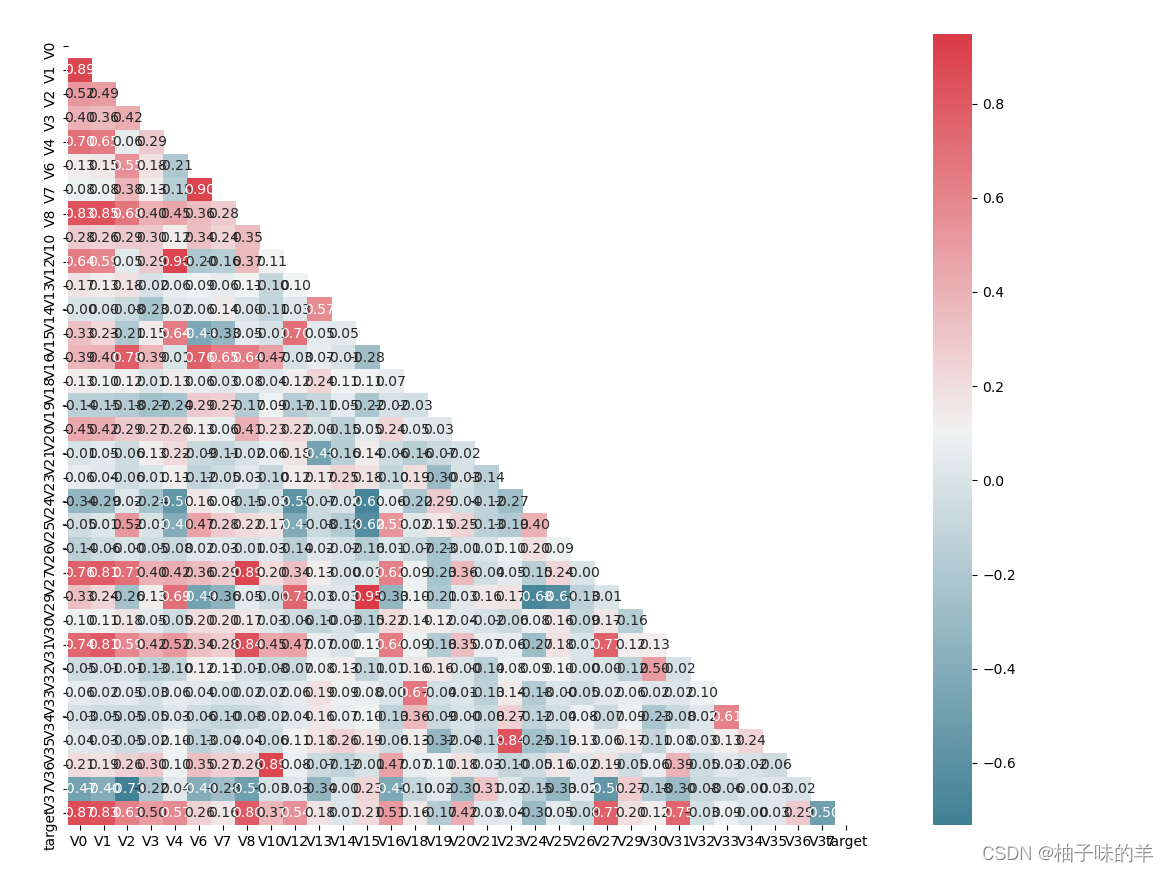
#%%找出相关程度 plt.figure(figsize=(20, 16)) # 指定绘图对象宽度和高度 colnm = train_data.columns.tolist() # 列表头 mcorr = train_data[colnm].corr(method="spearman") # 相关系数矩阵,即给出了任意两个变量之间的相关系数 mask = np.zeros_like(mcorr, dtype=np.bool) # 构造与mcorr同维数矩阵 为bool型 mask[np.triu_indices_from(mask)] = True # 角分线右侧为True cmap = sns.diverging_palette(220, 10, as_cmap=True) # 返回matplotlib colormap对象 g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f') # 热力图(看两两相似度) plt.show()
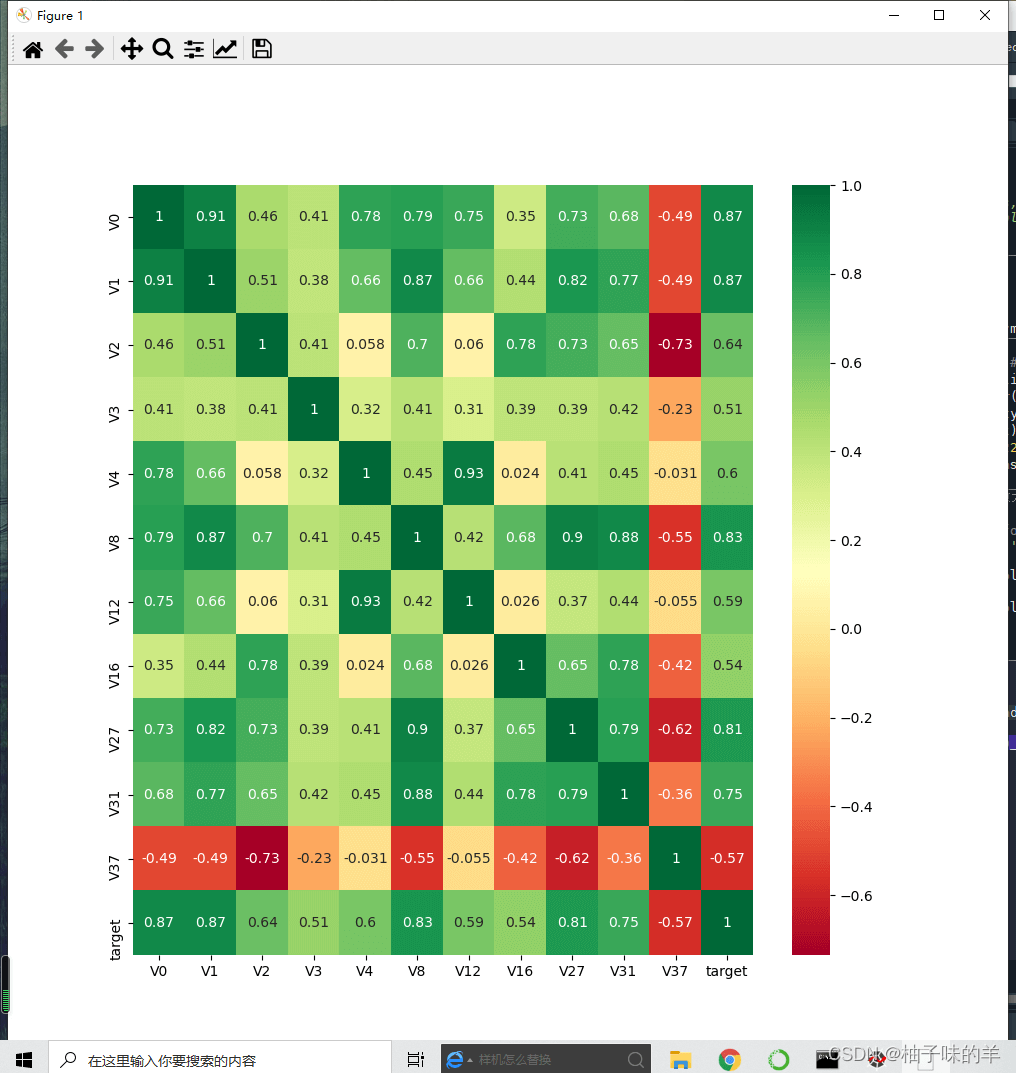
#%%查找特征变量和target变量相关系数大于0.5的特征变量 #寻找K个最相关的特征信息 k = 10 # number of variables for heatmap cols = train_corr.nlargest(k, 'target')['target'].index cm = np.corrcoef(train_data[cols].values.T) hm = plt.subplots(figsize=(10, 10))#调整画布大小 hm = sns.heatmap(train_data[cols].corr(),annot=True,square=True) plt.show()

threshold = 0.5 corrmat = train_data.corr() top_corr_features = corrmat.index[abs(corrmat["target"])>threshold] plt.figure(figsize=(10,10)) g = sns.heatmap(train_data[top_corr_features].corr(),annot=True,cmap="RdYlGn")
#%% Threshold for removing correlated variables
threshold = 0.05
# Absolute value correlation matrix
corr_matrix = train_data.corr().abs()
drop_col=corr_matrix[corr_matrix["target"]<threshold].index
#%%删除相关性小于0.05的列
train_data=train_data.drop(columns=drop_col)
test_data=test_data.drop(columns=drop_col)
#%%将train和test合并
train_x=train_data.drop(['target'],axis=1)
data_all=pd.concat([train_x,test_data])
#%%标准化
cols_numeric=list(data_all.columns)
def scale_minmax(col):
return (col-col.min())/(col.max()-col.min())
data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)
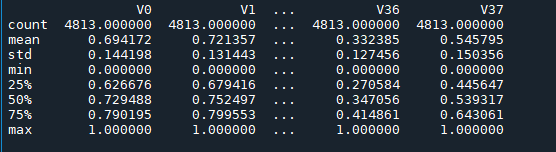
print(data_all[cols_numeric].describe())
train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_minmax,axis=0)
test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_minmax,axis=0)
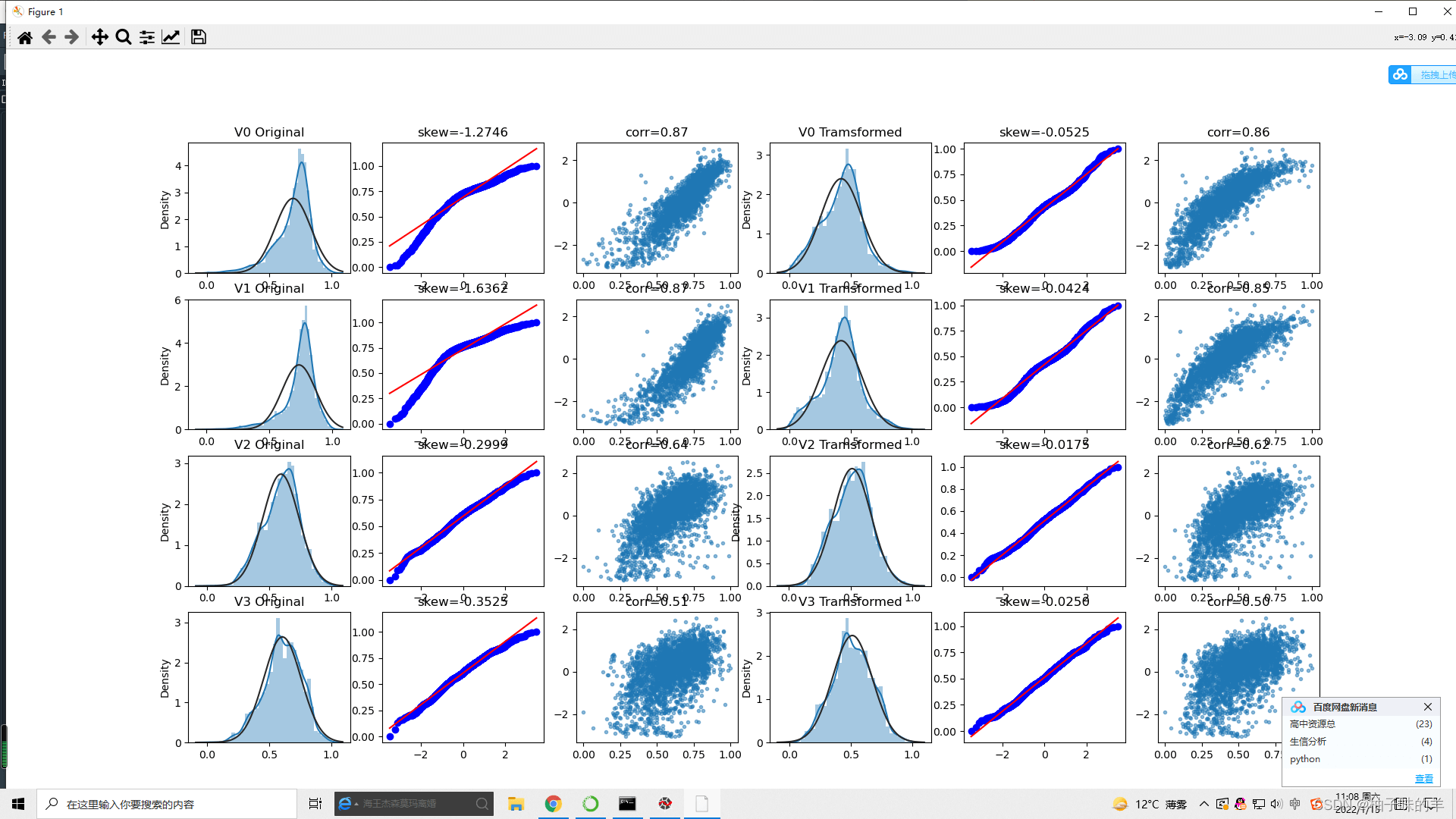
#%%查看v0-v3四个特征的箱盒图,查看其分布是否符合正态分布
cols_numeric_0to4 = cols_numeric[0:4]
## Check effect of Box-Cox transforms on distributions of continuous variables
train_data_process = pd.concat([train_data_process, train_data['target']], axis=1)
fcols = 6
frows = len(cols_numeric_0to4)
plt.figure(figsize=(4*fcols,4*frows))
i=0
for var in cols_numeric_0to4:
dat = train_data_process[[var, 'target']].dropna()
i+=1
plt.subplot(frows,fcols,i)
sns.distplot(dat[var] , fit=stats.norm);
plt.title(var+' Original')
plt.xlabel('')
i+=1
plt.subplot(frows,fcols,i)
_=stats.probplot(dat[var], plot=plt)
plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
plt.xlabel('')
plt.ylabel('')
i+=1
plt.subplot(frows,fcols,i)
plt.plot(dat[var], dat['target'],'.',alpha=0.5)
plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))
i+=1
plt.subplot(frows,fcols,i)
trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
trans_var = scale_minmax(trans_var)
sns.distplot(trans_var , fit=stats.norm);
plt.title(var+' Tramsformed')
plt.xlabel('')
i+=1
plt.subplot(frows,fcols,i)
_=stats.probplot(trans_var, plot=plt)
plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
plt.xlabel('')
plt.ylabel('')
i+=1
plt.subplot(frows,fcols,i)
plt.plot(trans_var, dat['target'],'.',alpha=0.5)
plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))
三、特征优化
import pandas as pd
train_data_file = "D:\Python\ML\data\zhengqi_train.txt"
test_data_file = "D:\Python\ML\data\zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
#%%定义特征构造方法,构造特征
epsilon=1e-5
#组交叉特征,可以自行定义,如增加: x*x/y, log(x)/y 等等,使用lambda函数更方便快捷
func_dict = {
'add': lambda x,y: x+y,
'mins': lambda x,y: x-y,
'div': lambda x,y: x/(y+epsilon),
'multi': lambda x,y: x*y
}
#%%定义特征构造函数
def auto_features_make(train_data,test_data,func_dict,col_list):
train_data, test_data = train_data.copy(), test_data.copy()
for col_i in col_list:
for col_j in col_list:
for func_name, func in func_dict.items():
for data in [train_data,test_data]:
func_features = func(data[col_i],data[col_j])
col_func_features = '-'.join([col_i,func_name,col_j])
data[col_func_features] = func_features
return train_data,test_data
#%%对训练集和测试集进行特征构造
train_data2, test_data2 = auto_features_make(train_data,test_data,func_dict,col_list=test_data.columns)
四、对特征构造后的训练集和测试集进行主成分分析
#%%PCA from sklearn.decomposition import PCA #主成分分析法 #PCA方法降维 pca = PCA(n_components=500) train_data2_pca = pca.fit_transform(train_data2.iloc[:,0:-1]) test_data2_pca = pca.transform(test_data2) train_data2_pca = pd.DataFrame(train_data2_pca) test_data2_pca = pd.DataFrame(test_data2_pca) train_data2_pca['target'] = train_data2['target'] X_train2 = train_data2[test_data2.columns].values y_train = train_data2['target']
五、使用LightGBM模型进行训练和预测
#%%使用lightgbm模型对新构造的特征进行模型训练和评估
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
import lightgbm as lgb
import numpy as np
# 5折交叉验证
kf = KFold(len(X_train2), shuffle=True, random_state=2019)
#%%
# 记录训练和预测MSE
MSE_DICT = {
'train_mse':[],
'test_mse':[]
}
# 线下训练预测
for i, (train_index, test_index) in enumerate(kf.split(X_train2)):
# lgb树模型
lgb_reg = lgb.LGBMRegressor(
learning_rate=0.01,
max_depth=-1,
n_estimators=5000,
boosting_type='gbdt',
random_state=2019,
objective='regression',
)
# 切分训练集和预测集
X_train_KFold, X_test_KFold = X_train2[train_index], X_train2[test_index]
y_train_KFold, y_test_KFold = y_train[train_index], y_train[test_index]
# 训练模型
lgb_reg.fit(
X=X_train_KFold,y=y_train_KFold,
eval_set=[(X_train_KFold, y_train_KFold),(X_test_KFold, y_test_KFold)],
eval_names=['Train','Test'],
early_stopping_rounds=100,
eval_metric='MSE',
verbose=50
)
# 训练集预测 测试集预测
y_train_KFold_predict = lgb_reg.predict(X_train_KFold,num_iteration=lgb_reg.best_iteration_)
y_test_KFold_predict = lgb_reg.predict(X_test_KFold,num_iteration=lgb_reg.best_iteration_)
print('第{}折 训练和预测 训练MSE 预测MSE'.format(i))
train_mse = mean_squared_error(y_train_KFold_predict, y_train_KFold)
print('------\n', '训练MSE\n', train_mse, '\n------')
test_mse = mean_squared_error(y_test_KFold_predict, y_test_KFold)
print('------\n', '预测MSE\n', test_mse, '\n------\n')
MSE_DICT['train_mse'].append(train_mse)
MSE_DICT['test_mse'].append(test_mse)
print('------\n', '训练MSE\n', MSE_DICT['train_mse'], '\n', np.mean(MSE_DICT['train_mse']), '\n------')
print('------\n', '预测MSE\n', MSE_DICT['test_mse'], '\n', np.mean(MSE_DICT['test_mse']), '\n------')

..... 不想等它跑完了,会一直跑到score不再变化或者round=100的时候为止~
加载全部内容