Python OpenCV傅里叶变换
小白YouCans 人气:0二维离散傅里叶变换(DFT)
对于二维图像处理,通常使用 x , y x, yx,y 表示离散的空间域坐标变量,用 u , v u,vu,v 表示离散的频率域变量。二维离散傅里叶变换(DFT)和反变换(IDFT)为:

二维离散傅里叶变换也可以用极坐标表示:

傅里叶频谱(Fourier spectrum)为:
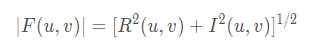
傅里叶相位谱(Fourier phase spectrum)为:

傅里叶功率谱(Fourier power spectrum)为:
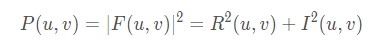
空间取样和频率间隔是相互对应的,频率域所对应的离散变量间的间隔为:Δu=1/MΔT, Δυ=1/NΔZ。即:频域中样本之间的间隔,与空间样本之间的间隔及样本数量的乘积成反比。
空间域滤波器和频率域滤波器也是相互对应的,二维卷积定理是在空间域和频率域滤波之间建立等价关系的纽带:

这表明 F 和 H 分别是 f 和 h 的傅里叶变换;f 和 h 的空间卷积的傅里叶变换,是它们的变换的乘积。
OpenCV 实现图像傅里叶变换(cv.dft)
使用 OpenCV 中的 cv.dft() 函数也可以实现图像的傅里叶变换,cv.idft() 函数实现图像傅里叶逆变换。
函数说明:
cv.dft(src[, dst[, flags[, nonzeroRows]]]) → dst cv.idft(src[, dst[, flags[, nonzeroRows]]]) → dst
参数说明:
src:输入图像,单通道灰度图像,使用 np.float32 格式
dst:输出图像,图像大小与 src 相同,数据类型由 flag 决定
flag:转换标识符
cv.DFT_INVERSE:用一维或二维逆变换取代默认的正向变换
cv.DFT_SCALE:缩放比例标识,根据元素数量求出缩放结果,常与DFT_INVERSE搭配使用
cv.DFT_ROWS: 对输入矩阵的每行进行正向或反向的傅里叶变换,常用于三维或高维变换等复杂操作
cv.DFT_COMPLEX_OUTPUT:对一维或二维实数数组进行正向变换,默认方法,结果是由 2个通道表示的复数阵列,第一通道是实数部分,第二通道是虚数部分
cv.DFT_REAL_OUTPUT:对一维或二维复数数组进行逆变换,结果通常是一个尺寸相同的复数矩阵
注意事项:
1.输入图像 src 是 np.float32 格式,如图像使用 np.uint8 格式则必须先转换 np.float32 格式。
2.默认方法 cv.DFT_COMPLEX_OUTPUT 时,输入 src 是 np.float32 格式的单通道二维数组,输出 dst 是 2个通道的二维数组,第一通道 dft[:,:,0] 是实数部分,第二通道 dft[:,:,1] 是虚数部分。
3.不能直接用于显示图像。可以使用 cv.magnitude() 函数将傅里叶变换的结果转换到灰度 [0,255]。
4.idft(src, dst, flags) 等价于 dft(src, dst, flags=DFT_INVERSE)。
5.OpenCV 实现傅里叶变换,计算速度比 Numpy 更快。
转换标识符为 cv.DFT_COMPLEX_OUTPUT 时,cv.dft() 函数的输出是 2个通道的二维数组,使用 cv.magnitude() 函数可以实现计算二维矢量的幅值 。
函数说明:
cv.magnitude(x, y[, magnitude]) → dst
参数说明:
x:一维或多维数组,也表示复数的实部,浮点型
y:一维或多维数组,也表示复数的虚部,浮点型,数组大小必须与 x 相同
dst:输出数组,数组大小和数据类型与 x 相同,运算公式为:

傅里叶变换及相关操作的取值范围可能不适于图像显示,需要进行归一化处理。 OpenCV 中的 cv.normalize() 函数可以实现图像的归一化。
函数说明:
cv.normalize(src, dst[, alpha[, beta[, norm_type[, dtype[, mask]]]]]) → dst
参数说明:
src:输入图像
dst:输出结果,与输入图像同尺寸同类型
alpha:归一化后的最小值,可选项,默认值为0
beta:归一化后的最大值,可选项,默认值为1
norm_type:归一化类型
- NORM_INF:Linf 范数(绝对值的最大值)
- NORM_L1:L1 范数(绝对值的和)
- NORM_L2:L2 范数(欧几里德距离),默认类型
- NORM_MINMAX:线性缩放,常用类型
dtype:可选项,默认值 -1,表示输出矩阵与输入图像类型相同
mask:掩模遮罩,可选项,默认无遮罩
傅里叶变换在理论上需要O(MN)²次运算,非常耗时;快速傅里叶变换只需要O(MN㏒(MN)) 次运算就可以完成。
OpenCV 中的傅里叶变换函数 cv.dft() 对于行数和列数都可以分解为2^p*3^q*5^r的矩阵的计算性能最好。为了提高运算性能,可以对原矩阵的右侧和下方补 0,以满足该分解条件。OpenCV 中的 cv.getOptimalDFTSize() 函数可以实现图像的最优 DFT 尺寸扩充,适用于 cv.dft() 和 np.fft.fft2()。
函数说明:
cv.getOptimalDFTSize(versize) → retval
参数说明:
versize:数组大小
retval:DFT 扩充的最优数组大小
示例代码
# 8.11:OpenCV 实现二维图像的离散傅里叶变换
imgGray = cv2.imread("../images/Fig0424a.tif", flags=0) # flags=0 读取为灰度图像
# cv2.dft 实现图像的傅里叶变换
imgFloat32 = np.float32(imgGray) # 将图像转换成 float32
dft = cv2.dft(imgFloat32, flags=cv2.DFT_COMPLEX_OUTPUT) # 傅里叶变换
dftShift = np.fft.fftshift(dft) # 将低频分量移动到频域图像的中心
# 幅度谱
# ampSpe = np.sqrt(np.power(dft[:,:,0], 2) + np.power(dftShift[:,:,1], 2))
dftAmp = cv2.magnitude(dft[:,:,0], dft[:,:,1]) # 幅度谱,未中心化
dftShiftAmp = cv2.magnitude(dftShift[:,:,0], dftShift[:,:,1]) # 幅度谱,中心化
dftAmpLog = np.log(1 + dftShiftAmp) # 幅度谱对数变换,以便于显示
# 相位谱
phase = np.arctan2(dftShift[:,:,1], dftShift[:,:,0]) # 计算相位角(弧度制)
dftPhi = phase / np.pi*180 # 将相位角转换为 [-180, 180]
print("dftMag max={}, min={}".format(dftAmp.max(), dftAmp.min()))
print("dftPhi max={}, min={}".format(dftPhi.max(), dftPhi.min()))
print("dftAmpLog max={}, min={}".format(dftAmpLog.max(), dftAmpLog.min()))
# cv2.idft 实现图像的逆傅里叶变换
invShift = np.fft.ifftshift(dftShift) # 将低频逆转换回图像四角
imgIdft = cv2.idft(invShift) # 逆傅里叶变换
imgRebuild = cv2.magnitude(imgIdft[:,:,0], imgIdft[:,:,1]) # 重建图像
plt.figure(figsize=(9, 6))
plt.subplot(231), plt.title("Original image"), plt.axis('off')
plt.imshow(imgGray, cmap='gray')
plt.subplot(232), plt.title("DFT Phase"), plt.axis('off')
plt.imshow(dftPhi, cmap='gray')
plt.subplot(233), plt.title("Rebuild image with IDFT"), plt.axis('off')
plt.imshow(imgRebuild, cmap='gray')
plt.subplot(234), plt.title("DFT amplitude spectrum"), plt.axis('off')
plt.imshow(dftAmp, cmap='gray')
plt.subplot(235), plt.title("DFT-shift amplitude"), plt.axis('off')
plt.imshow(dftShiftAmp, cmap='gray')
plt.subplot(236), plt.title("Log-trans of DFT amp"), plt.axis('off')
plt.imshow(dftAmpLog, cmap='gray')
plt.tight_layout()
plt.show()

加载全部内容