Java 图的进阶

时间:2022-05-23 龍弟-idea 人气:0

有向图

有向图的定义及相关术语

定义∶ 有向图是一副具有方向性的图，是由一组顶点和一组有方向的边组成的，每条方向的边都连着一对有序的顶点。

出度∶ 由某个顶点指出的边的个数称为该顶点的出度。

入度: 指向某个顶点的边的个数称为该顶点的入度。

有向路径︰由一系列顶点组成，对于其中的每个顶点都存在一条有向边，从它指向序列中的下一个顶点。

有向环∶ —条至少含有一条边，且起点和终点相同的有向路径。

一副有向图中两个顶点v和w可能存在以下四种关系:

1.没有边相连;

⒉存在从v到w的边v—>w;

3.存在从w到v的边w—>V;

4.既存在w到v的边，也存在v到w的边，即双向连接;

理解有向图是一件比较简单的，但如果要通过眼睛看出复杂有向图中的路径就不是那么容易了。

有向图API设计

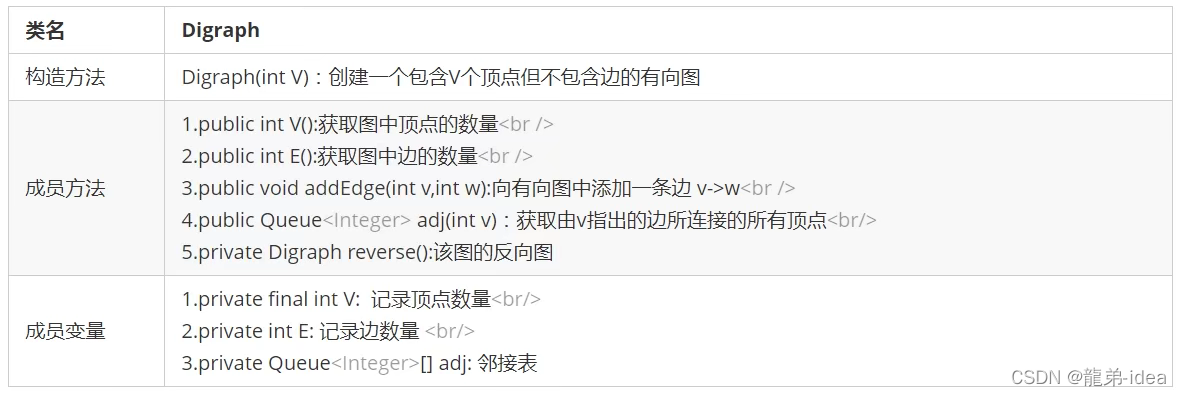
在api中设计了一个反向图，其因为有向图的实现中，用adj方法获取出来的是由当前顶点v指向的其他顶点，如果能得到其反向图，就可以很容易得到指向v的其他顶点。

有向图的实现

// 有向图
 
public class Digraph {
    // 记录顶点的数量
     
    private final int V;
 
    //记录边的数量
    private int E;
 
    //定义有向图的邻接表
    private Queue <Integer>[] adj;
 
    public Digraph (int v) {
        //初始化顶点数量
        this.V = v;
        //初始化边的数量
        this.E = 0;
        //初始化邻接表
        adj = new LinkedList[v];
        //初始化邻接表的空队列
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkedList<>();
        }
    }
    public int V () {
        return V;
    }
    public int E () {
        return E;
    }
 
    //添加一条 v -> w的有向边
    public void addEage (int v , int w) {
        adj[v].add(w);
        ++E;
    }
 
    //获取顶点v 指向的 所有顶点
    public Queue<Integer> adj (int v) {
        return adj[v];
    }
 
    //将有向图 反转 后返回
    public Digraph reverse () {
        //创建一个反向图
        Digraph reverseDigraph = new Digraph(V);
        //获取原来有向图的每个结点
        for (int i = 0; i < V; i++) {
            //获取每个结点 邻接表的所有结点
            for (Integer w : adj[i]) {
                //反转图记录下 w -> v
                reverseDigraph.adj(w).add(i);
            }
        }
        return reverseDigraph;
    }
}

拓扑排序

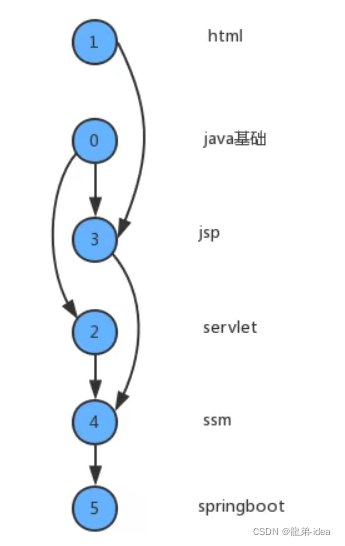
在现实生活中，我们经常会同一时间接到很多任务去完成，但是这些任务的完成是有先后次序的。以我们学习java学科为例，我们需要学习很多知识，但是这些知识在学习的过程中是需要按照先后次序来完成的。从java基础，到jsp/servlet，到ssm，到springboot等是个循序渐进且有依赖的过程。在学习jsp前要首先掌握java基础和html基础，学习ssm框架前要掌握jsp/servlet之类才行。

为了简化问题，我们使用整数为顶点编号的标准模型来表示这个案例:

此时如果某个同学要学习这些课程，就需要指定出一个学习的方案，我们只需要对图中的顶点进行排序，让它转换为一个线性序列，就可以解决问题，这时就需要用到一种叫拓扑排序的算法。

拓扑排序图解

给定一副有向图，将所有的顶点排序，使得所有的有向边均从排在前面的元素指向排在后面的元素，此时就可以明确的表示出每个顶点的优先级。下列是一副拓扑排序后的示意图︰

检测有向图中的环

如果学习x课程前必须先学习y课程，学习y课程前必须先学习z课程，学习z课程前必须先学习x课程，那么一定是有问题了，我们就没有办法学习了，因为这三个条件没有办法同时满足。其实这三门课程x、y、z的条件组成了一个环︰

因此，如果我们要使用拓扑排序解决优先级问题，首先得保证图中没有环的存在。

检测有向环的API设计

检测有向环实现

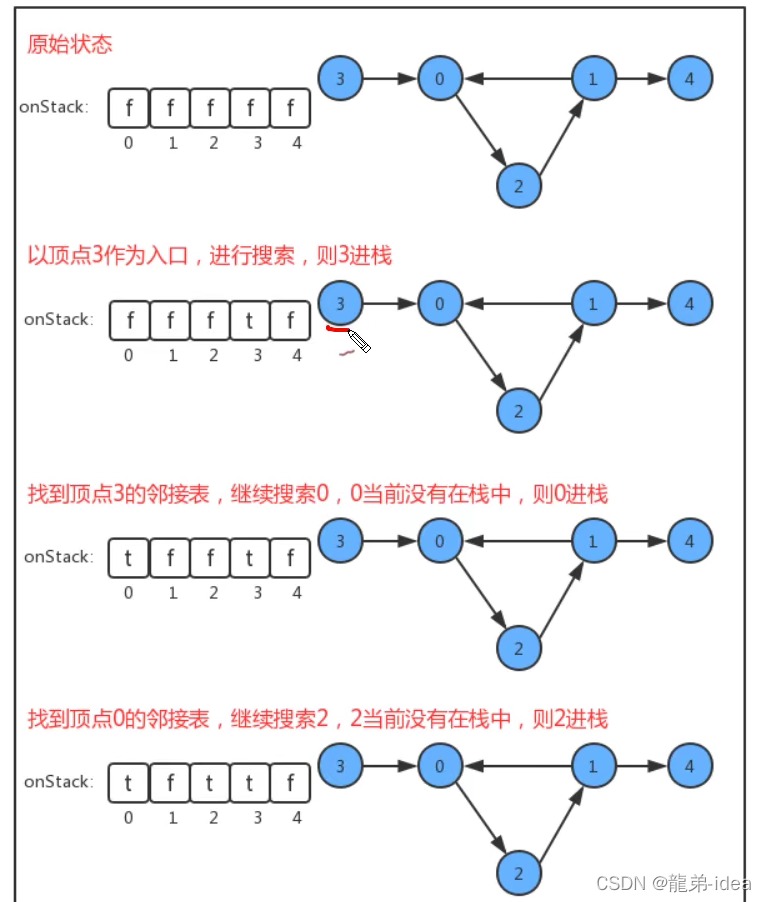
在API中添加了onStack[]布尔数组，索引为图的顶点，当我们深度搜索时︰

1.在如果当前顶点正在搜索，则把对应的onStack数组中的值改为true，标识进栈;

2.如果当前顶点搜索完毕，则把对应的onStack数组中的值改为false，标识出栈;

3.如果即将要搜索某个顶点，但该顶点已经在栈中，则图中有环;

代码

 
/**
 *  检查图中是否存在环
 */
public class DirectedCycle {
    /**
     * 索引代表顶点，用来记录顶点是否被搜索过
     */
    private boolean[] marked;
 
    /**
     * 判断图中是否有环
     */
    private boolean hasCycle;
 
    /**
     * 采用栈的思想，记录当前顶点是否已经存在 当前搜索的的路径上
     * 存在则可以判断 图中是存在环的
     */
    private boolean[] onStack;
 
    /**
     * 判断传入的有向图 是否存在环
     * @param G
     */
    public DirectedCycle (Digraph G) {
        marked = new boolean[G.V()];
        onStack = new boolean[G.V()];
        hasCycle = false;
        //因为不知道从那个点出发 可能存在环
        //所以需要从所有的顶点都出发搜索 判断是否存在环
        for (int i = 0; i < G.V(); i++) {
            dfs(G,i);
        }
    }
 
    /**
     * 采用深度搜索 判断有向图是否存在环
     * onStack 入栈出栈 然后判断当前搜索的顶点是否已经在搜索路径上
     *
     * @param G
     * @param v
     */
    private void dfs (Digraph G,int v) {
        //标记顶点已经搜索过
        marked[v] = true;
        for (Integer adj : G.adj(v)) {
            //判断v 是否已经在搜索的路径上了
            if(marked[adj] && onStack[adj]) {
                //存在环
                hasCycle = true;
            }else {
                //采用回溯的思路
                //让顶点入栈
                onStack[adj] = true;
                dfs(G,adj);
                //回溯 顶点出栈
                onStack[adj] = false;
            }
        }
    }
 
    /**
     * 判断是否存在环
     * @return
     */
    public boolean hasCycle(){
        return hasCycle;
    }
 
}

基于深度优先的顶点排序

如果要把图中的顶点生成线性序列其实是一件非常简单的事，之前我们学习并使用了多次深度优先搜索，我们会发现其实深度优先搜索有一个特点，那就是在一个连通子图上，每个顶点只会被搜索一次，如果我们能在深度优先搜索的基础上，添加一行代码，只需要将搜索的顶点放入到线性序列的数据结构中，我们就能完成这件事。

顶点排序API设计

顶点排序实现

在API的设计中，我们添加了一个栈reversePost用来存储顶点，当我们深度搜索图时，每搜索完毕一个顶点，把该顶点放入到reversePost中，这样就可以实现顶点排序。

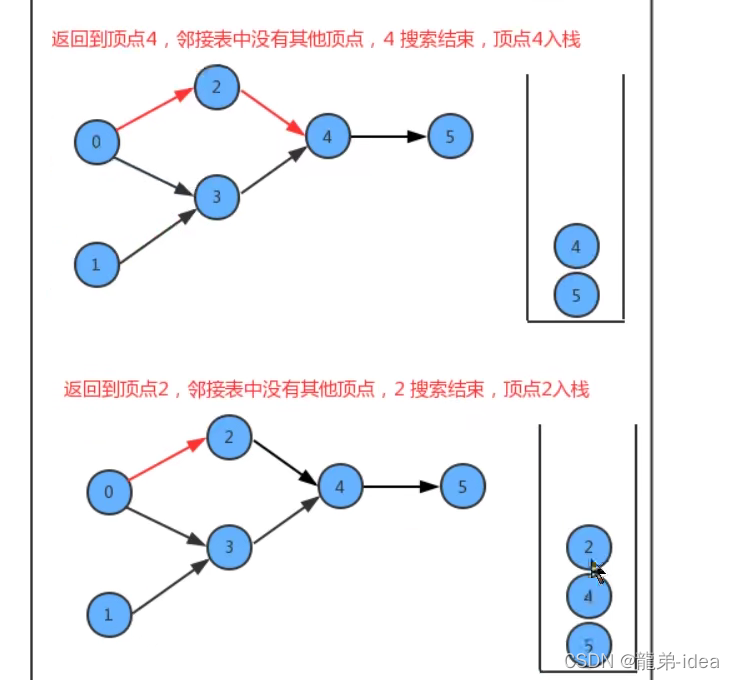
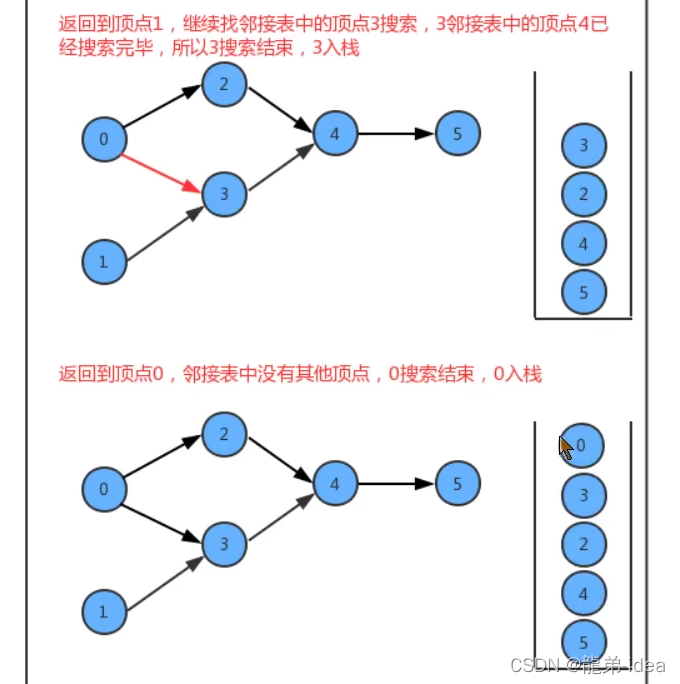
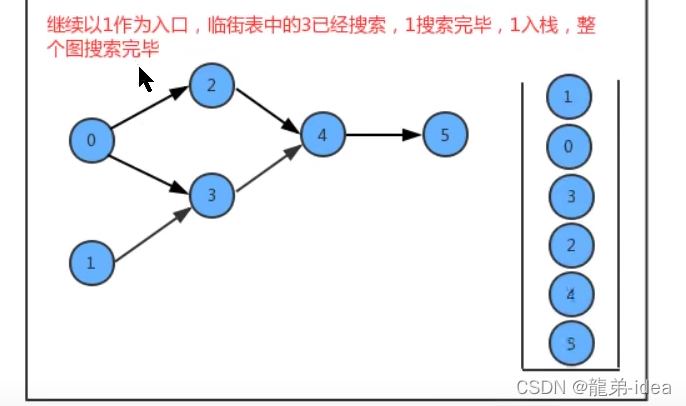
代码:

 
/**
 * 深度优先搜索 的顶点排序
 */
public class DepthFirstOrder {
    /**
     * 索引代表顶点 ，用来记录顶点是否已经被搜索过了
     */
    private boolean[] marked;
 
    /**
     * 使用栈记录深度优先搜索下的顶点
     */
    private Stack<Integer> reversePost;
 
    public DepthFirstOrder (Digraph G) {
        marked = new boolean[G.V()];
        reversePost = new Stack<>();
        for (int i = 0; i < G.V(); i++) {
            //如果顶点已经被搜索过则不用
            if(!marked[i])
                dfs(G,i);
        }
    }
 
    /**
     * 基于深度优先搜索，生成顶点线性序列
     * @param G
     * @param v
     */
    private void dfs (Digraph G, int v) {
        //标记顶点已经被搜索过
        marked[v] =  true;
        for (Integer w : G.adj(v)) {
            if(!marked[w])
                dfs(G,w);
        }
        //记录到线性序列中
        reversePost.push(v);
    }
 
    /**
     * 获取顶点线性序列
     * @return
     */
    private Stack<Integer> ReversePost() {
        return reversePost;
    }
}

加载全部内容