Python直方图均衡化
MrWinter 人气:01.点算子
点算子是两个像素灰度值间的映射关系,属于像素的逐点运算,相邻像素不参与运算。点算子是最简单的图像处理手段,如:亮度调整、对比度调整、颜色变换、直方图均衡化等等。
2.线性灰度变换
线性灰度变换表达为:
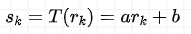
其中rk、sk分别为输入、输出点像素灰度值。
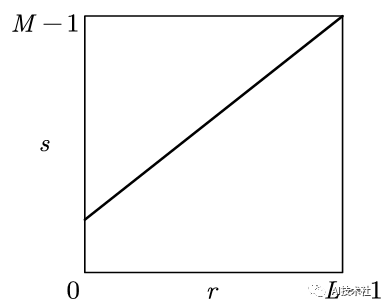
▲图2.1 线性灰度变换
当a>1时,输出图像像素灰度范围扩大,图像对比度增强,当a<1时反之。这是因为人眼不易区分相近的灰度值,因此若图像灰度值范围较小,观感上细节不够清晰。当a=1、b≠0时,点算子使图像灰度整体上移或下移,即整体变亮或变暗。

▲图2.2 图像对比度(左为弱对比度,右为强对比度)
3.直方图均衡化
下图再次给出了关于图像对比度的例子。
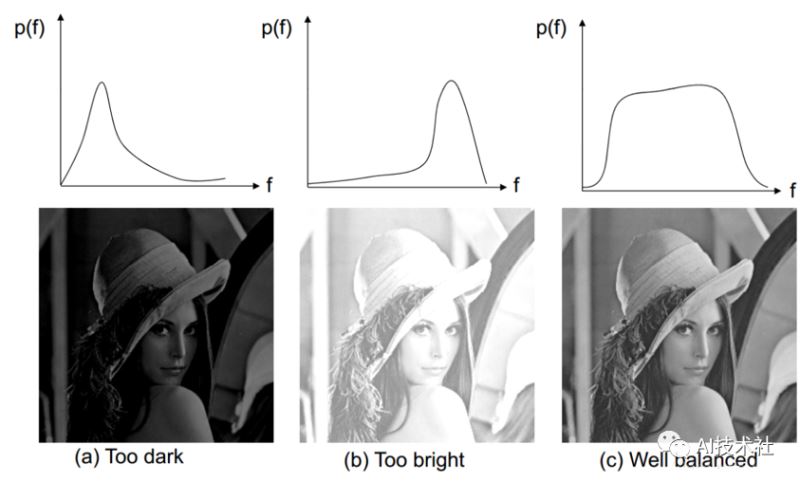
▲图3.1 图像对比度示例
直方图均衡化是以累计分布函数为核心,将原始图像灰度直方图从比较集中的某个灰度区间,非线性地映射为在全部灰度范围内的较均匀分布,从而增强对比度。
下面阐述直方图均衡化的数学原理。首先作原始图像灰度的概率直方图如图。
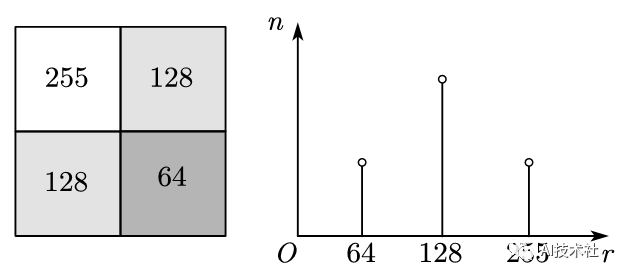
▲图3.2 直方图均衡化原理
设输入像素灰度值为rk,累计分布函数为
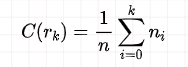
其中ni为图像中灰度值为ri的像素频数,n为图像像素总数。设输出像素灰度值为sk,像素范围为smin-smax。期望输出灰度直方图是均匀分布,即
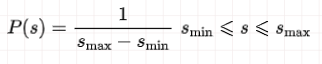
令C(sk)=C(rk),即得
所以最终直方图均衡化的点算子为
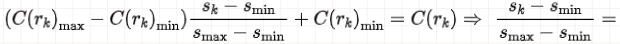
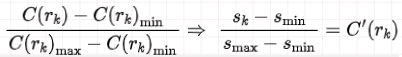
所以最终直方图均衡化的点算子为
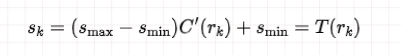
4.代码实战
按照前文的原理编写累积分布函数计算公式,以及均衡化算子
# 计算累计分布函数 def C(rk): # 读取图片灰度直方图 # bins为直方图直方柱的取值向量 # hist为bins各取值区间上的频数取值 hist, bins = np.histogram(rk, 256, [0, 256]) # 计算累计分布函数 return hist.cumsum()
# 计算灰度均衡化映射
def T(rk):
cdf = C(rk)
# 均衡化
cdf = (cdf - cdf.min()) * (255 - 0) / (cdf.max() - cdf.min()) + 0
return cdf.astype('uint8')
均衡化时直接调用函数即可,下面给出完整代码
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 计算累计分布函数
def C(rk):
# 读取图片灰度直方图
# bins为直方图直方柱的取值向量
# hist为bins各取值区间上的频数取值
hist, bins = np.histogram(rk, 256, [0, 256])
# 计算累计分布函数
return hist.cumsum()
# 计算灰度均衡化映射
def T(rk):
cdf = C(rk)
# 均衡化
cdf = (cdf - cdf.min()) * (255 - 0) / (cdf.max() - cdf.min()) + 0
return cdf.astype('uint8')
# 读取图片
img = cv.imread('1.png', 0)
# 将二维数字图像矩阵转变为一维向量
rk = img.flatten()
# 原始图像灰度直方图
plt.hist(rk, 256, [0, 255], color = 'r')
cv.imshow("原图像",img)
# 直方图均衡化
imgDst = T(rk)[img]
cv.imshow("直方图均衡化后的图像",imgDst)
plt.hist(imgDst.flatten(), 256, [0, 255], color = 'b')
plt.show()
看看效果:
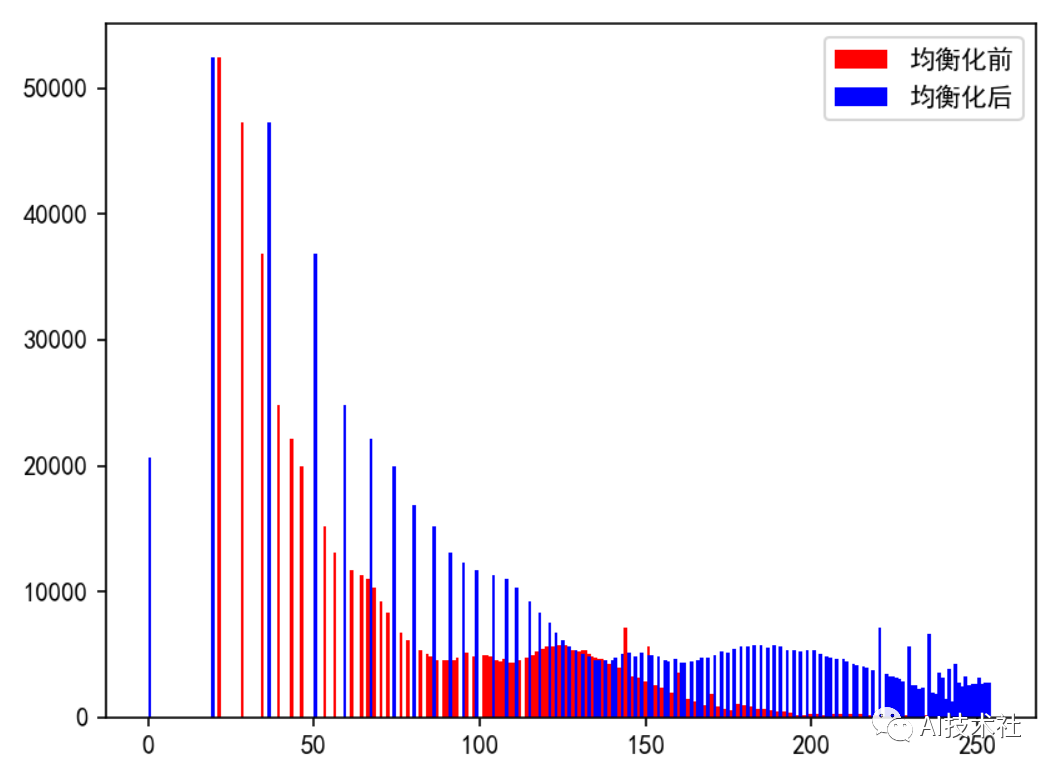
▲图4.1 直方图均衡化效果(灰度直方图)

▲图4.2 均衡化前

▲图4.3 均衡化后
加载全部内容