Python光学仿真衍射算法
微小冷 人气:0对衍射最经典的解释是Huygens-Fresnel原理,Huygens认为波阵面上每一点都会成为新的波源,这些子波源的相互干涉就形成了衍射。这显然是一种离散的观点,仿佛是专门为程序员准备的一样。
假设一束光打在一个方形孔上,这个方形孔被细分成 n×n个网格,那么每个网格都相当于是一个小孔,而这些小孔的互相干涉,即为衍射。随着网格不断被细分,最终可以逼近真实的衍射情形。那么,假设矩孔处为等相位面,其网格坐标为 (i,j),到衍射屏距离为 d d d,那么对于衍射屏上任意一点P(x,y),其光强为

同理,我们刚刚写下的平面矩孔光强叠加也出现了问题,如果我们默认矩孔上每个格点都是一个点光源,那么打在衍射屏上之后,应该遵从球面波的衰减原则。又因为这种假设其实忽略了从光源射到矩孔过程中的光线的传播方向,所以应该有一个倾斜因子,即 ( i , j ) 点打在 ( x , y )点的光强为

#基尔霍夫衍射,衍射屏坐标范围-dGrid:dGrid,光源坐标(0,0)
#简单的矩孔衍射,dSource为光源到小孔的距离;dScreen为衍射屏到小孔距离
#dHole为矩孔网格尺寸;dGrid为衍射屏网格尺寸;nGrid为网格数目
def squareDiff(dSource=1,dScreen=1.4,dWave=1e-6,
dHole=3e-5,nGrid=100,dGrid=1e-5):
nX,nY = nGrid*np.array([1,1])
axisX = np.arange(-nX,nX+1)*dGrid
axisY = np.arange(-nY,nY+1)*dGrid
xAxis,yAxis = np.meshgrid(axisX,axisY) #此为衍射屏的x坐标
axisX = np.arange(-nX,nX+1)*dHole
axisY = np.arange(-nY,nY+1)*dHole
xHole,yHole = np.meshgrid(axisX,axisY) #此为矩孔的x坐标
dArrS = np.sqrt(xHole**2+yHole**2+dSource**2) #孔平面到光源的距离
nSide = int(nGrid*2+1) #格点个数
pane = np.zeros([nSide,nSide]) #衍射屏强度
for m in range(nSide):
for n in range(nSide):
dArr = np.sqrt((xHole-xAxis[m,n])**2+(yHole-yAxis[m,n])**2+dScreen**2)
pane[m,n] = np.sum(
np.cos(np.pi*2*(dArr+dArrS)/dWave)/dArr/dArrS)
pane = np.abs(pane)
pane = pane/np.max(np.array(pane))
fig = plt.figure()
ax = axd(fig)
ax.plot_surface(xAxis,yAxis,pane)
plt.show()
return pane, xAxis, yAxis
其结果为
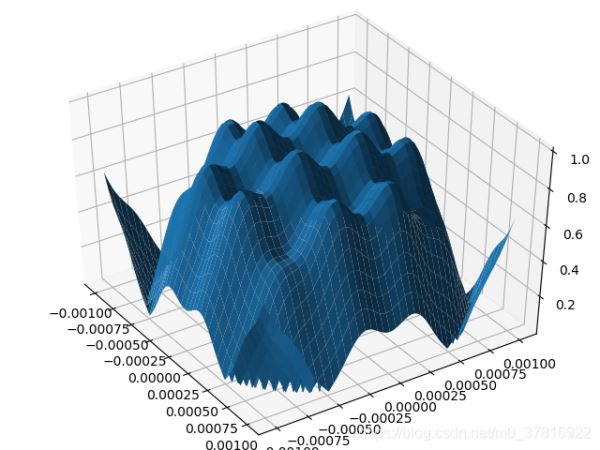

故可定义矩阵索引
#输入对于M*M矩阵的第一个值到N*N矩阵的距离,返回M(m,n)的距离矩阵
def getDisMat(dMat,N,m,n):
dMat = np.mat(dMat)
A = dMat[1:m,1:n]
B = dMat[1:m,0:N-n+1]
C = dMat[0:N-m+1,1:n]
D = dMat[0:N-m+1,0:N-n+1]
return np.vstack((np.hstack((np.flip(A),np.flipud(B))),np.hstack((np.fliplr(C),D)))) #stack矩阵拼接,flip翻转矩阵
相应地算法改为(其他位置不变)
dArrS = np.sqrt(xHole**2+yHole**2+dSource**2) #孔平面到光源的距离
dScreen = np.sqrt( #衍射平上第(0,0)个点的距离矩阵
(xHole-xAxis[0,0])**2+(yHole-yAxis[0,0])**2+dScreen**2)
nSide = int(nGrid*2+1) #格点个数
pane = np.zeros([nSide,nSide]) #衍射屏强度
for m in range(nSide):
for n in range(nSide):
dArr = getDisMat(dScreen,nSide,m,n)
但这种优化是极其有限的,这是直观无脑的思维方式所带来的麻烦。在接下来的傅里叶光学中,我们将继续处理衍射的计算问题。
加载全部内容