Python归一化算法 Python实现归一化算法详情
紧到长不胖 人气:0想了解Python实现归一化算法详情的相关内容吗,紧到长不胖在本文为您仔细讲解Python归一化算法的相关知识和一些Code实例,欢迎阅读和指正,我们先划重点:Python实现归一化算法,Python归一化算法,下面大家一起来学习吧。
1.前言
归一化算法Normalization将数据处理成量纲一直的数据,一般限定在[0,1]、[-1,1]
一般在进行建模的时候需要进行数据归一化处理,
原因如下:
- 降低计算难度
- 有可能提高模型的预测精度
- 消除量纲影响
下面介绍三种常见的标准化方法,分别是最大最小值、正态中心化、小数点定标
2.Min-Max方法
2.1 公式
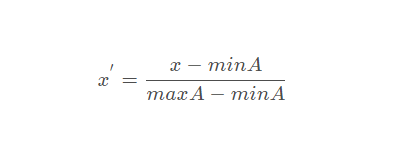
2.2 算法实现逻辑
- 1.找一组数据的最大最小值
- 2.利用公式归一化
- 3.输入结果(为了方便可视化展示,我们设计了代码)
2.3 代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1.最小最大标准化
Data = np.array([[0.2,0.9,29],
[0.9,0.1,100],
[0.5,0.5,30]]) #最小-最大归一化算法
# 1.1数据转化
def MinMax(data):
min = 0
max = 1
C = data[:,2]
min = np.min(C)
max = np.max(C)
for one in data:
one[2] = (one[2]-min) / (max-min)
print('转化后的矩阵:\n',data)
return data
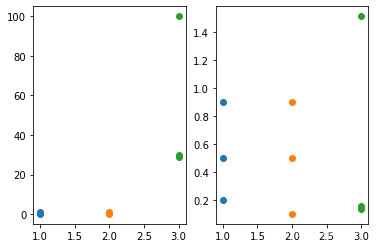
# 1.2可视化
def ShowData(Data,ShowD1):
length = len(Data)
X = np.ones(Data.shape[0])
plt.figure(1)
plt.subplot(121)
for i in range(length):
plt.scatter(X*(i+1),Data[:,i])
plt.subplot(122)
for i in range(length):
plt.scatter(X*(i+1),ShowD1[:,i])
plt.show()
ShowData(Data,MinMax(Data.copy()))转化后的矩阵:
[[0.2 0.9 0. ]
[0.9 0.1 1. ]
[0.5 0.5 0.01408451]]

2.4局限
- 数据规模过大不适应
- 数据归一化后范围在[0,1],对于一些有负有正数的原始数据慎用
3 Z-score标准化
3.1 公式
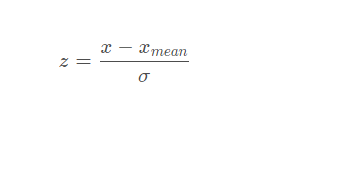
3.2 算法实现逻辑
- 输入数据
- 求取数据的均值、方法,在利用中心化公式计算
- 输出结果
3.3 代码
def Zscore(data):
x_mean = np.mean(data[:2])
length = len(data[:,2])
vari = np.sqrt((np.sum((data[:2]-x_mean)**2))/length)
print('方差:',vari)
data[:,2] = (data[:,2]-x_mean)/vari
print('Z-score标准化后的矩阵是',data)
return data
ShowData(Data,Zscore(Data.copy()))方差: 51.569160680908254
Z-score标准化后的矩阵是 [[0.2 0.9 0.13864876]
[0.9 0.1 1.5154406 ]
[0.5 0.5 0.15804019]]
3.4 局限
- 对样本量少的数据,表现不好
- 标准化后范围在有负有正,范围在[-1,1]
4 小数定标法
4.1 公式
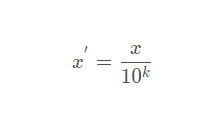
4.2 算法实现逻辑
- 输入数据
- 绝对值化,最大值
- 将每个数除以最大值的数量级
- 输入数据
4.3 代码实现
# 小数定标归一化算法
def Decimals(data):
C = np.abs(data[:,2])
max = int(np.sort(C)[-1]) # 按从小到大排序,取最后一位,及最大值
k = len(str(max))
print('绝对值最大的位数:\n',k)
data[:2] = data[:,2] /(10**k)
print('小数点定标准化后的矩阵:\n',data)
return data
ShowData(Data,Decimals(Data.copy()))绝对值最大的位数:
3
小数点定标准化后的矩阵:
[[2.9e-02 1.0e-01 3.0e-02]
[2.9e-02 1.0e-01 3.0e-02]
[5.0e-01 5.0e-01 3.0e+01]]
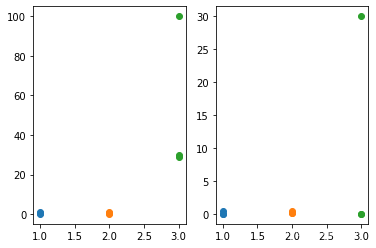
4.4 局限
- 受到最大值影响较大
加载全部内容