Python 数据结构 Python数据结构之树的全面解读

前言

提示：以下是本篇文章正文内容

🧡基本概念

🌳树的定义

树是n（n≥0）个结点的有限集合，n = 0时，称为空树，这是一种特殊情况

在任意一棵非空树中应满足：
①有且仅有一个特定的称为根的结点
②当n > 1时，其余结点可分为m（m > 0）个互不相交的有限集合T1，T2，…，Tm，其中每个集合本身又是一棵树，并且称为根结点的子树==

∅ 空树——结点数为0的树

非空树的特性：

有且仅有一个根节点
除了根节点外，任何一个结点都有且仅有一个前驱
每个结点可以有0个或多个后继

🌲基本术语

1.度

(1)结点的度：结点所拥有的子树的个数

(2)树的度：树中各结点度的最大值

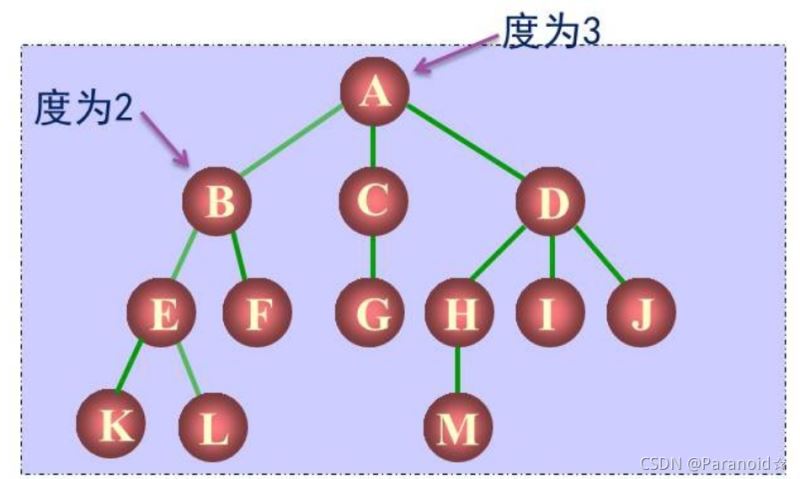
A的度为3，同时也是树的度，B的度为2

2.叶子节点和分支节点
(1)叶子节点
度为0的节点，也称为终端结点

(2)分支节点
度不为0的节点，也称为非终端结点

在上图中，K,L,M,F,G,I,J均为叶子节点

3.双亲与孩子
(1)祖先结点：对于任何节点n ，它的祖先是位于根到节点n之间的路径上的节点

(2)子孙结点：一个结点含有的子树的根结点的子节点

在树中，如果有一条路径从节点x到节点y,则称x为y的祖先，y为x的子孙

(3)双亲结点（父节点）：若一个结点含有子结点，则这个结点称为其子结点的父节点

(4)孩子结点：一个结点含有的子树的根结点称为该结点的子结点

(5)兄弟结点：具有相同父结点的结点互称为兄弟结点

(6)堂兄弟结点：如果树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点
B,C,D互为兄弟节点，E,G,I互为堂兄弟节点，B为E,F的父节点，而E,F为B的子节点

(4)树的深度
节点所在层数：根节点的层数为1，对于其他任何节点，若某节点在第K层，则其孩子节点在K+1层

树的深度：树中所有节点的最大层数，也称为高度
在上图中，树的深度为4

(5)树的类型
有序树：树中结点的各子树从左至右是有次序的，不能互换
无序树：树中结点的各子树从左至右是无次序的，可以互换

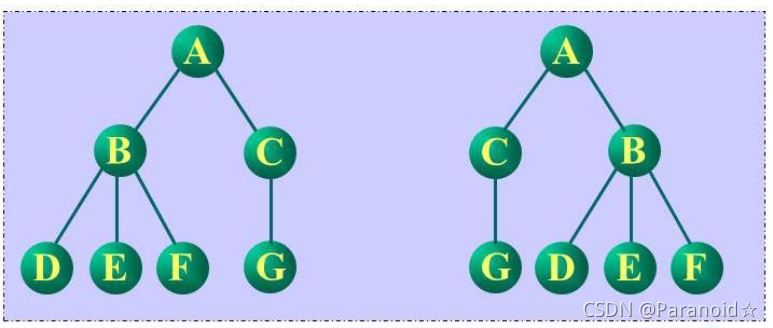
注：在数据结构中，一般的讨论的一般是有序树

(6)森林
森林是m（m≥0）棵互不相交的树的集合，m可为0，空森林

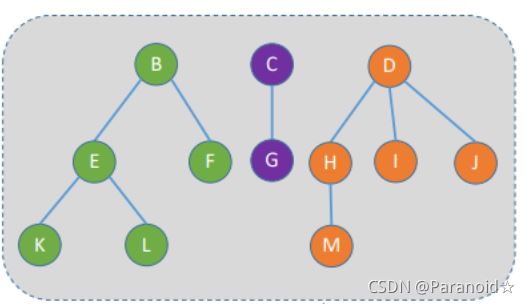
💚树的逻辑结构

树的遍历：从根节点出发，按照某种次序访问树中所有的节点，使得每个节点被访问一次且仅被访问一次

访问：抽象操作，可以是对节点进行的各种处理，这里简化为输出节点的数据

遍历的实质：树的结构(非线性结构) – > 线性结构

树通常有前序(根)遍历，后序(根)遍历，层序(次)遍历三种

🍉前序遍历

树的前序遍历操作定义为：若树为空，则空操作返回；否则:
(1)先访问根节点
(2)然后按照从左到右的顺序前序遍历根节点的每一颗子树

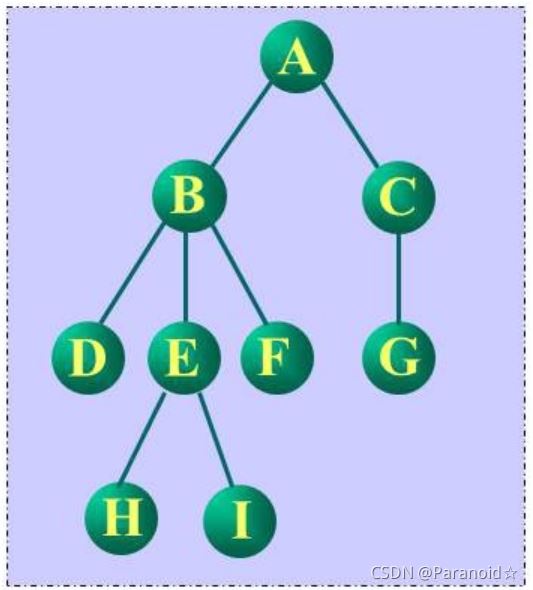
如图前序遍历序列：A–>B–>D–>E–>H–>I–>F–>C–>G

🍓后序遍历

树的后序遍历操作定义为：若树为空，则空操作返回；否则:
(1)先按照从左到右的顺序后序遍历根节点的每一颗子树
(2)最后访问根节点

如图后序遍历序列：D–>H–>I–>E–>F–>B–>G–>C–A

🍒层序遍历

树的层序遍历操作定义为：从树的第一层(即根节点）开始，自上而下的逐层遍历，在同一层中，按照从左到右的顺序对节点逐个访问

如图层序遍历序列：A–>B–>C–>D–>E–>F–>G–>H–>I

💜树的存储结构

实现树的存储结构，关键在于表示树中的节点之间的关系

🍀双亲表示法

基本思想：用一维数组来存储树的各个节点（一般按层序存储），数组中的一个元素对应树中的一个节点，包括节点的数据信息和节点的双亲在数组中的下标。

节点结构

struct PNode
{
	DataType data; //数据域
	int parent;   //指针域，双亲在数组中的下标
}

树的双亲表示法实质上是一个静态链表
如图所示：

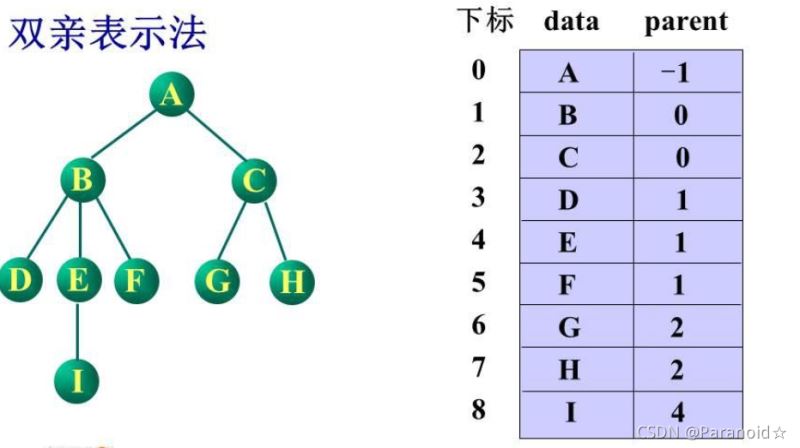
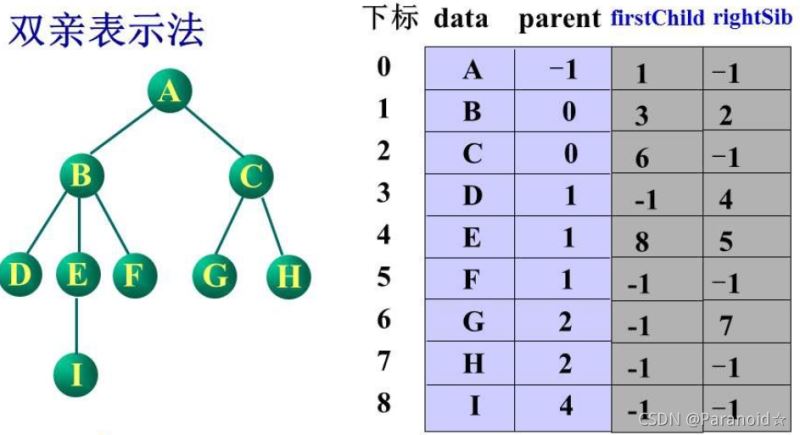
还可以将孩子节点或者兄弟节点的下标也进行存储

🍁孩子链表表示法

将结点的所有孩子放在一起，构成线性表

基本思想：把每个结点的孩子排列起来，看成是一个线性表，且以单链表存储，则n个结点共有n个孩子链表。这n个单链表共有n个头指针，这n个头指针又组成了一个线性表,为了便于进行查找采用顺序存储。最后, 将存放n个头指针的数组和存放n个结点的数组结合起来，构成孩子链表的表头数组

链表中的每个节点包含一个数据域和多个指针域，每个指针域指向该节点的一个孩子节点

方案一：
指针域的个数等于树的深度

缺点：浪费存储空间

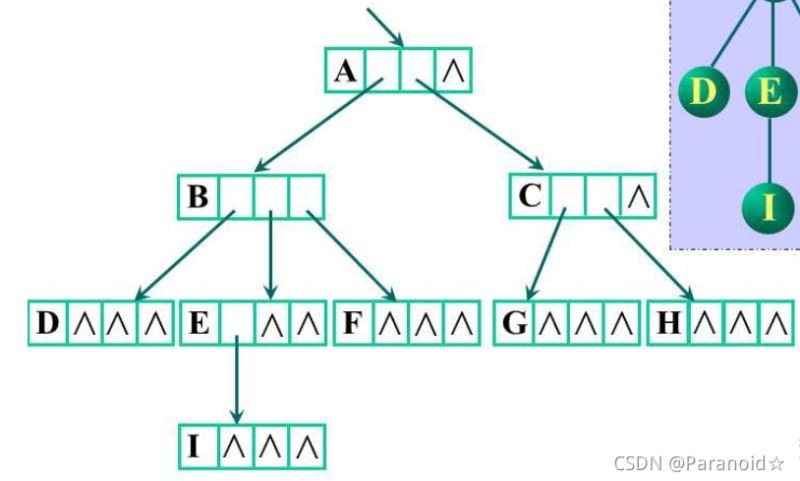
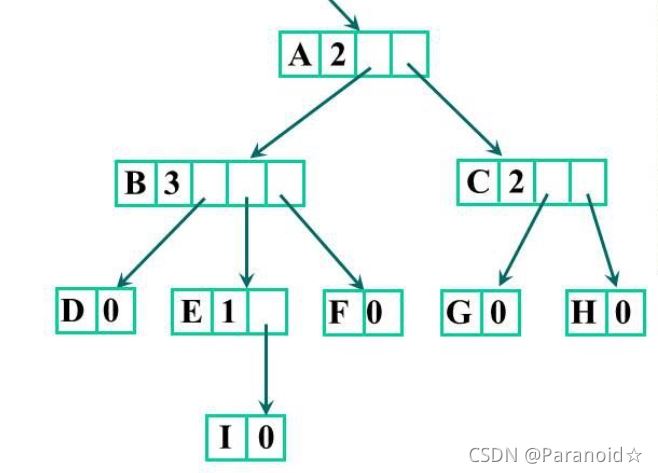
方案二：
指针域的个数等于该结点的度

缺点：每个结点结构不一致

孩子节点

struct CTNode
{
	int child;
	CTNode *next; // 指向下一个孩子结点的指针
}

表头结点

struct CBNode
{
	DataType data;
	CTNode *firstChild; // 每个链表的头指针
}

存储结构

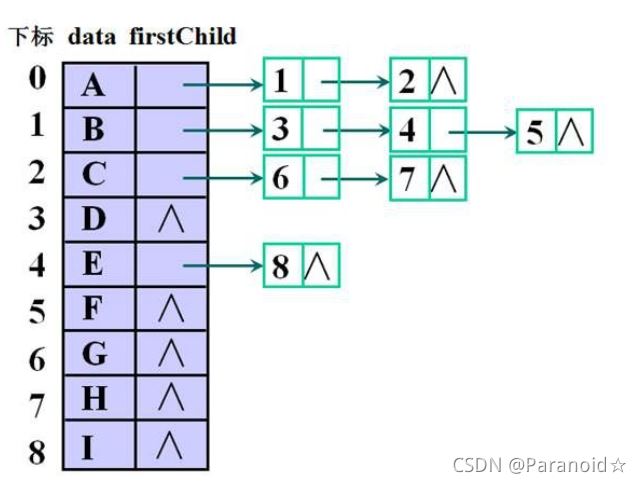
🍃双亲孩子表示法

在孩子链表中表头数组添加了节点的双亲结点

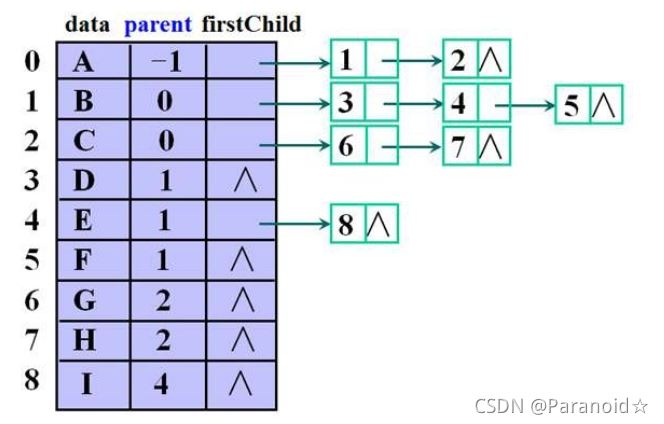
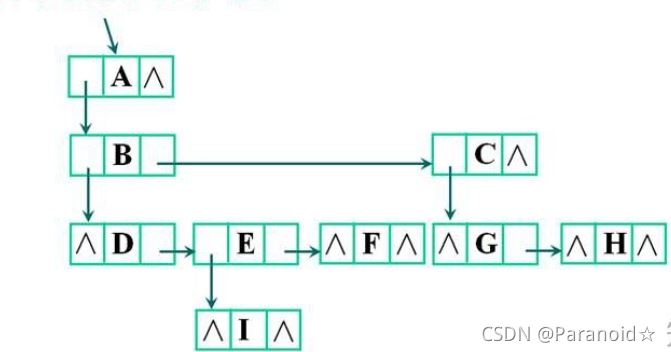
🍂孩子兄弟表示法

某节点的第一个孩子是唯一的，某一节点的右兄弟是唯一的，设置两个分别指向该节点的第一个孩子和右兄弟的指针

struct TNode
{
	DataType data;
	TNode *firstChild,*rightSib;
}

总结

提示：这里对文章进行总结：