PyTorch 逻辑斯蒂回归 PyTorch零基础入门之逻辑斯蒂回归

时间:2021-10-19 山顶夕景人气:0

想了解PyTorch零基础入门之逻辑斯蒂回归的相关内容吗，山顶夕景在本文为您仔细讲解PyTorch 逻辑斯蒂回归的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：PyTorch,逻辑斯蒂回归,Python,PyTorch，下面大家一起来学习吧。

学习总结

（1）和上一讲的模型训练是类似的，只是在线性模型的基础上加个sigmoid，然后loss函数改为交叉熵BCE函数（当然也可以用其他函数），另外一开始的数据y_data也从数值改为类别0和1（本例为二分类，注意x_data和y_data这里也是矩阵的形式）。

一、sigmoid函数

logistic function是一种sigmoid函数（还有其他sigmoid函数），但由于使用过于广泛，pytorch默认logistic function叫为sigmoid函数。还有如下的各种sigmoid函数：

在这里插入图片描述

二、和Linear的区别

逻辑斯蒂和线性模型的unit区别如下图：

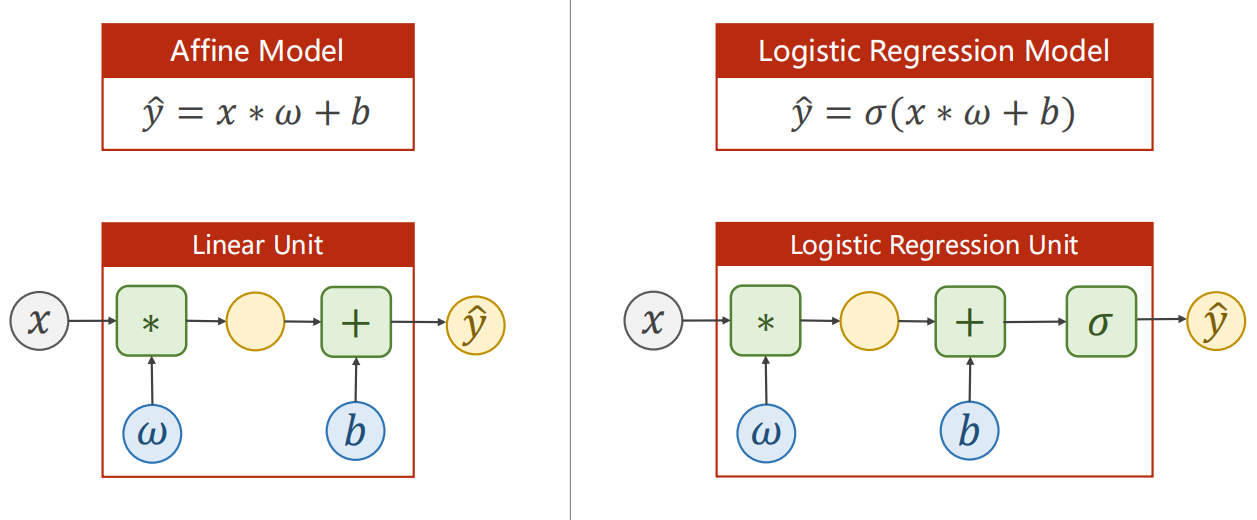
在这里插入图片描述

sigmoid函数是不需要参数的，所以不用对其初始化（直接调用nn.functional.sigmoid即可）。
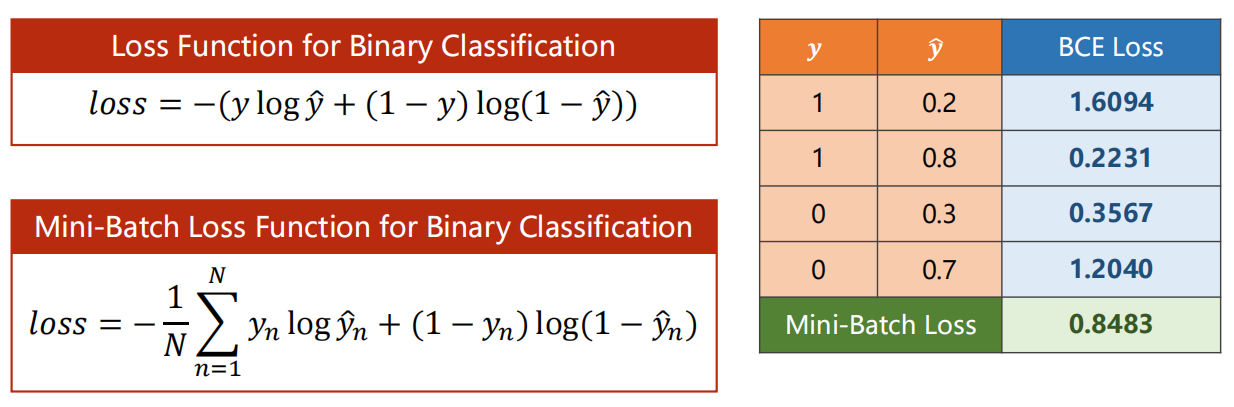
另外loss函数从MSE改用交叉熵BCE：尽可能和真实分类贴近。

在这里插入图片描述

如下图右方表格所示，当 y ^ \hat{y} y^越接近y时则BCE Loss值越小。

在这里插入图片描述

三、逻辑斯蒂回归（分类）PyTorch实现

# -*- coding: utf-8 -*-
"""
Created on Mon Oct 18 08:35:00 2021

@author: 86493
"""
import torch
import torch.nn as nn
import matplotlib.pyplot as plt  
import torch.nn.functional as F
import numpy as np

# 准备数据
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])


losslst = []

class LogisticRegressionModel(nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)
        
    def forward(self, x):
    	# 和线性模型的网络的唯一区别在这句，多了F.sigmoid
        y_predict = F.sigmoid(self.linear(x))
        return y_predict
    
model = LogisticRegressionModel()

# 使用交叉熵作损失函数
criterion = torch.nn.BCELoss(size_average = False)
optimizer = torch.optim.SGD(model.parameters(), 
                            lr = 0.01)

# 训练
for epoch in range(1000):
    y_predict = model(x_data)
    loss = criterion(y_predict, y_data)
    # 打印loss对象会自动调用__str__
    print(epoch, loss.item())
    losslst.append(loss.item())
    # 梯度清零后反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

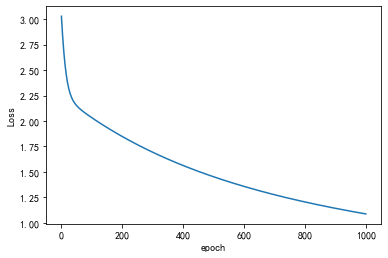
# 画图
plt.plot(range(1000), losslst)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()


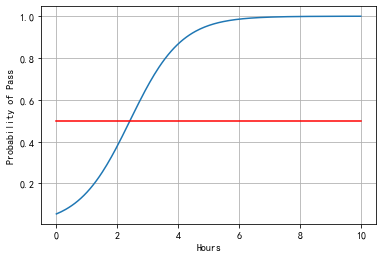
# test
# 每周学习的时间，200个点
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1))
y_t = model(x_t)
y = y_t.data.numpy()
plt.plot(x, y)
# 画 probability of pass = 0.5的红色横线
plt.plot([0, 10], [0.5, 0.5], c = 'r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

在这里插入图片描述

可以看出处于通过和不通过的分界线是Hours=2.5。

在这里插入图片描述

Reference

pytorch官方文档

加载全部内容