Turtle库实现对称勾股树 Python学习Turtle库画对称勾股树体会分形惊艳
Hann Yang 人气:0分形,具有以非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。分形(Fractal)一词,是芒德勃罗创造出来的,其原意具有不规则、支离破碎等意义。1973年,芒德勃罗(B.B.Mandelbrot)在法兰西学院讲课时,首次提出了分维和分形的设想。
分形是一个数学术语,也是一套以分形特征为研究主题的数学理论。分形理论既是非线性科学的前沿和重要分支,又是一门新兴的横断学科,是研究一类现象特征的新的数学分科,相对于其几何形态,它与微分方程与动力系统理论的联系更为显著。分形的自相似特征可以是统计自相似,构成分形也不限于几何形式,时间过程也可以,故而与鞅论关系密切。
分形几何是一门以不规则几何形态为研究对象的几何学。由于不规则现象在自然界普遍存在,因此分形几何学又被称为描述大自然的几何学。分形几何学建立以后,很快就引起了各个学科领域的关注。不仅在理论上,而且在实用上分形几何都具有重要价值。
——摘自百度百科


分形树是分形几何中的一小种类型,一棵分形树相当于一棵“满二叉树”。通常都用递归来实现,递归条件通常分两派,一派是用长度递减,直到长度不满足某个条件时退出;另一派则是按层数来递归,相当于“满二叉树”的层序遍历。前一派的长度递归相当于“满二叉树”的先序遍历,从根出发先左子树后右子树,每一棵子树都按这种“先根后左右”的顺序遍历。
举个例子:

源代码:
import turtle
def bintree(size):
angle = 60 # 分叉的角度
if size > 5: # 长度退出条件
turtle.forward(size)
turtle.left(angle)
bintree(size / 1.6)
turtle.right(angle*2)
bintree(size / 1.6)
turtle.left(angle)
turtle.backward(size)
def main():
turtle.speed(0)
turtle.hideturtle()
turtle.penup()
turtle.left(90)
turtle.backward(100)
turtle.showturtle()
turtle.pendown()
turtle.pensize(2)
turtle.color('green')
bintree(150)
turtle.done()
if __name__ == '__main__':
main()
以上代码中长度以等比数列递减,公比1/1.6;当然也可以改成等差数列形式。此方式缺点树的层数不能直接控制,需要用初始长度、递减公式和退出条件来计算得出。
勾股树,其实就是分形树的一种,只是不像上例一样简单地画2个分叉,而是画直角三角形加上各边上的正方形,就像平面几何中勾股定理证明时画的示意图。
以下是我用Turtle库画的一棵12层的对称勾股树,使用“层序遍历”方式:

根据二叉树的性质可知:12层的树会有 2^12 - 1 个正方形以及同样数量的三角形。时间复杂度为指数级,在关掉画笔踪迹开关的情况下画完此时耗时43秒。
简单点,就用一个6层的来示意一下其“层序”的过程:
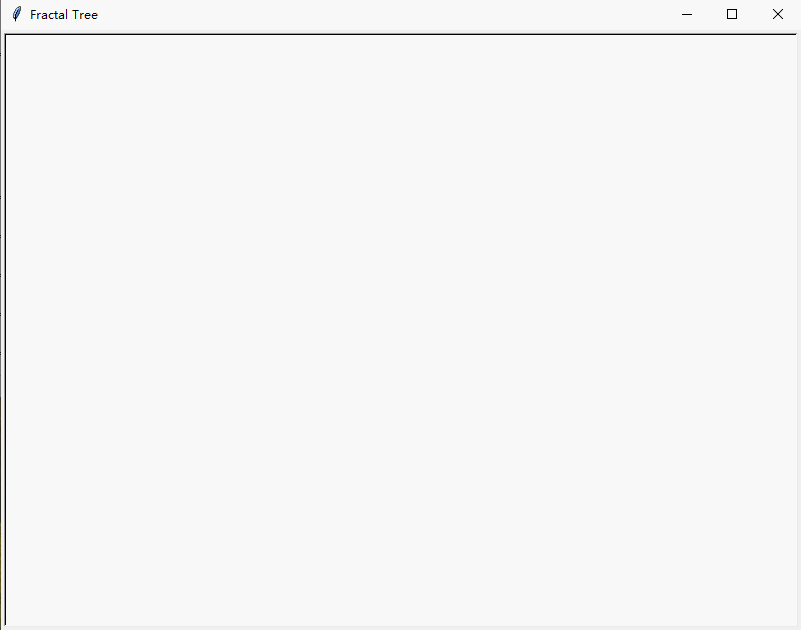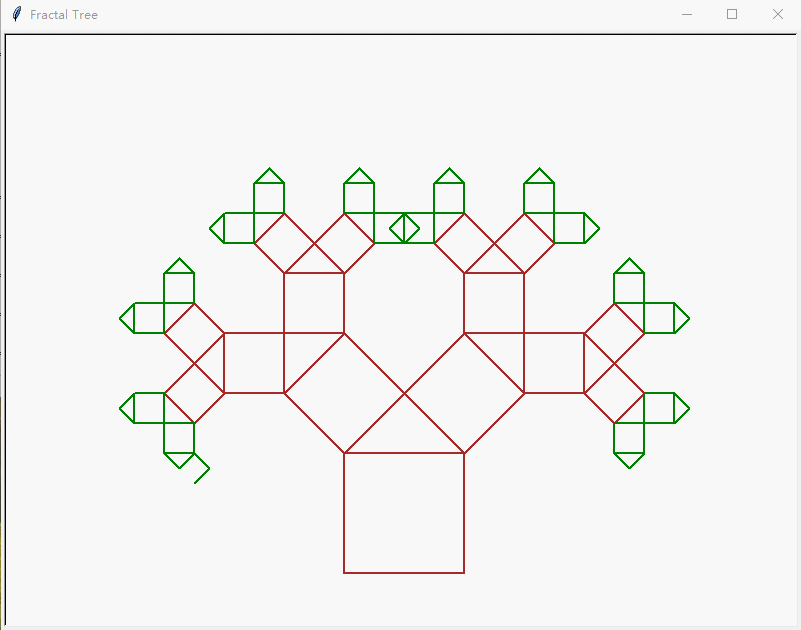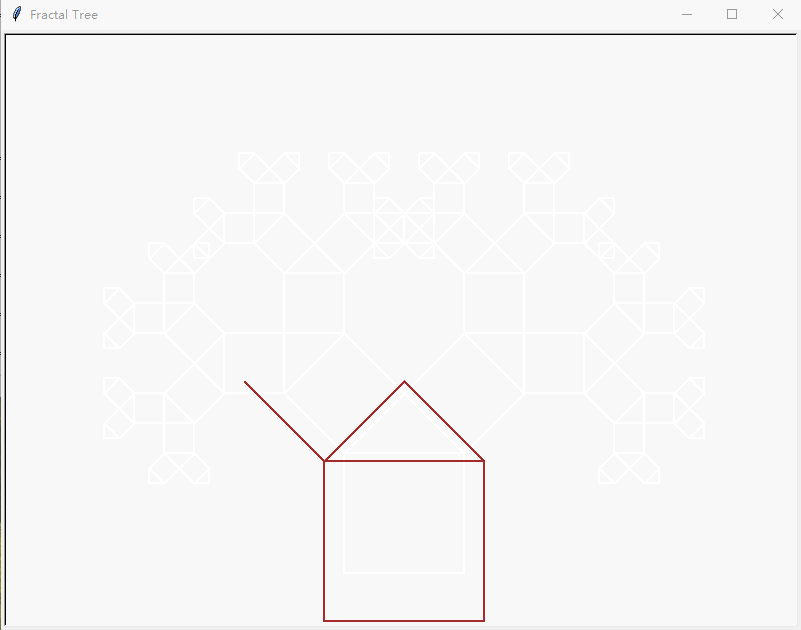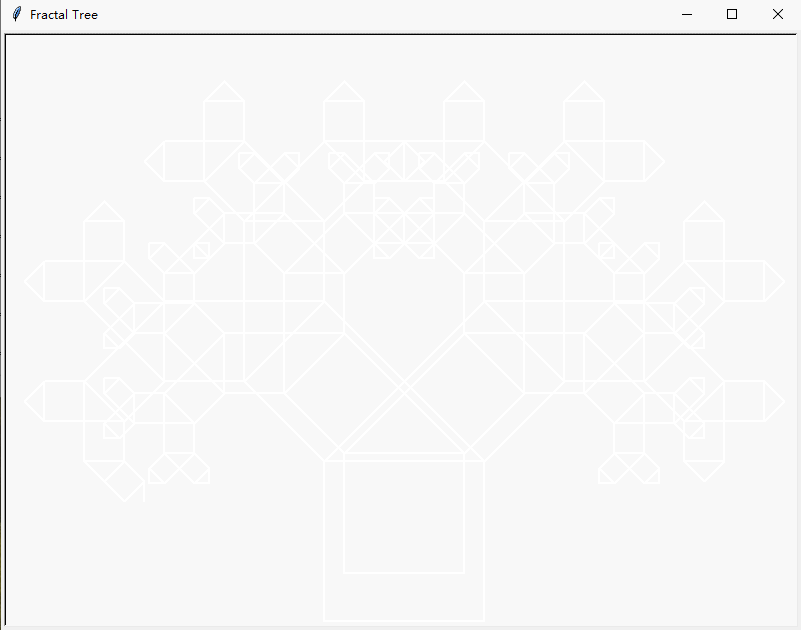
源代码:
from turtle import *
def Square(self,length):
for _ in range(5):
self.forward(length)
self.right(90)
def Triangle(self,length):
self.left(45)
self.forward(length/2**0.5)
self.right(90)
self.forward(length/2**0.5)
self.right(135)
self.forward(length)
def Move2Right(self,length):
self.back(length)
self.right(45)
self.forward(length/2**0.5)
self.right(90)
def Recursive(n, tracer, length):
if n<1: return
tracers = []
for left in tracer:
if n<3: left.pencolor('green')
else: left.pencolor('brown')
Square(left, length)
Triangle(left, length)
right = left.clone()
left.right(45)
Move2Right(right, length)
tracers.append(left)
tracers.append(right)
Recursive(n-1, tracers, length/2**0.5)
def Setup(self, length, speed):
self.hideturtle()
self.speed(speed)
self.penup()
self.goto(-length*0.5, -length*1.8)
self.seth(90)
self.pensize(2)
self.pendown()
def main(level, length, speed=-1):
setup(800,600)
title('Fractal Tree')
if speed==-1: tracer(0)
else: tracer(1)
t = Turtle()
Setup(t, length, speed)
from time import sleep
sleep(2)
Recursive(level, list([t]), length)
done()
bye()
if __name__ == '__main__':
main(6,150,10)
主函数: main(level, length, speed=-1)
参数:
level: 树的层数
length: 最底层正方形的边长
speed: 1~10,画笔速度递增;=0时速度最快;=-1时关闭画笔踪迹。
本篇完,其他分形图待继......
更多关于Turtle库实现对称勾股树的资料请关注其它相关文章!
加载全部内容