JAVA快速排序 JAVA十大排序算法之快速排序详解
阿粤Ayue 人气:0快速排序
快速排序是对冒泡排序的一种改进,也是采用分治法的一个典型的应用。JDK中Arrays的sort()方法,具体的排序细节就是使用快速排序实现的。
从数组中任意选取一个数据(比如数组的第一个数或最后一个数)作为关键数据,我们称为基准数(pivot,或中轴数),然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序,也称为分区(partition)操作。
问题
若给定一个无序数组 [8, 5, 6, 4, 3, 1, 7, 2],并指定一个数为基准,拆分数组使得左侧的数都小于等于它 ,右侧的数都大于它。
基准的选取最优的情况是基准值刚好取在无序区数值的中位数,这样能够最大效率地让两边排序,同时最大地减少递归划分的次数,但是一般很难做到最优。基准的选取一般有三种方式:
- 选取数组的第一个元素
- 选取数组的最后一个元素
- 以及选取第一个、最后一个以及中间的元素的中位数(如4 5 6 7, 第一个4, 最后一个7, 中间的为5, 这三个数的中位数为5, 所以选择5作为基准)。
思路
- 随机选择数组的一个元素,比如 6 为基准,拆分数组同时引入一个初始指针,也叫分区指示器,初始指针指向 -1
- 将数组中的元素和基准数遍历比较
- 若当前元素大于基准数,不做任何变化
- 若当前元素小于等于基准数时,分割指示器右移一位,同时
- 当前元素下标小于等于分区指示器时,当前元素保持不动
- 当前元素下标大于分区指示器时,当前元素和分区指示器所指元素交换

荷兰国旗问题
荷兰的国旗是由红白蓝三种颜色构成,如图:

若现在给一个随机的图形,如下:

把这些条纹按照颜色排好,红色的在上半部分,白色的在中间部分,蓝色的在下半部分,这类问题称作荷兰国旗问题。
对应leetcode:颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
分析:
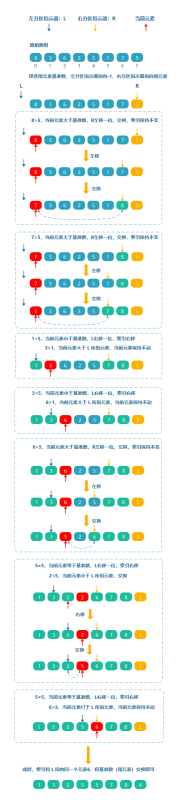
假如给定一个数组[8, 3, 6, 2, 5, 1, 7, 5],做如下操作:
1.随机选择数组的一个元素,比如 5 为基准,拆分数组同时引入一个左分区指示器,指向 -1,右分区指示器指向基准数(注:此时的基准数为尾元素)
2.若当前元素大于基准数,右分区指示器左移一位,当前元素和右分区指示器所指元素交换,
索引保持不变
3.若当前元素小于等于基准数时,左分区指示器右移一位,索引右移
- 当前元素大于等于左分区指示器所指元素,当前元素保持不动
- 当前元素小于左分区指示器所指元素,交换
简单来说就是,左分区指示器向右移动的过程中,如果遇到大于或等于基准数时,则停止移动,右分区指示器向左移动的过程中,如果遇到小于或等于主元的元素则停止移动。这种操作也叫双向快速排序。
代码实现
public class QuickSort {
public static final int[] ARRAY = {8, 5, 6, 4, 3, 1, 7, 2};
public static final int[] ARRAY2 = {8, 3, 6, 2, 5, 1, 7, 5};
private static int[] sort(int[] array, int left, int right) {
if (array.length < 1 || left > right) return null;
//拆分
int partitionIndex = partition(array, left, right);
//递归
if (partitionIndex > left) {
sort(array, left, partitionIndex - 1);
}
if (partitionIndex < right) {
sort(array, partitionIndex + 1, right);
}
return array;
}
/**
* 分区快排操作
*
* @param array 原数组
* @param left 左侧头索引
* @param right 右侧尾索引
* @return 分区指示器 最后指向基准数
*/
public static int partition(int[] array, int left, int right) {
//基准数下标---随机方式取值,也就是数组的长度随机1-8之间
int pivot = (int) (left + Math.random() * (right - left + 1));
//分区指示器索引
int partitionIndex = left - 1;
//基准数和尾部元素交换
swap(array, pivot, right);
//按照规定,如果当前元素大于基准数不做任何操作;
//小于基准数,分区指示器右移,且当前元素的索引大于分区指示器,交换
for (int i = left; i <= right; i++) {
if (array[i] <= array[right]) {//当前元素小于等于基准数
partitionIndex++;
if (i > partitionIndex) {//当前元素的索引大于分区指示器
//交换
swap(array, i, partitionIndex);
}
}
}
return partitionIndex;
}
/**
* 双向扫描排序
*/
public static int partitionTwoWay(int[] array, int left, int right) {
//基准数
int pivot = array[right];
//左分区指示器索引
int leftIndex = left - 1;
//右分区指示器索引
int rightIndex = right;
//索引
int index = left;
while (index < rightIndex) {
//若当前元素大于基准数,右分区指示器左移一位,当前元素和右分区指示器所指元素交换,索引保持不变
if (array[index] > pivot) {
swap(array, index, --rightIndex);
} else if (array[index] <= pivot) {//当前元素小于等于基准数时,左分割指示器右移一位,索引右移
leftIndex++;
index++;
//当前元素小于等于左分区指示器所指元素,交换
if (array[index] < array[leftIndex]) {
swap(array, index, leftIndex);
}
}
}
//索引和 L 指向同一个元素
swap(array, right, rightIndex);
return 1;
}
//交换
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void print(int[] array) {
for (int i : array) {
System.out.print(i + " ");
}
System.out.println("");
}
public static void main(String[] args) {
print(ARRAY);
System.out.println("============================================");
print(sort(ARRAY, 0, ARRAY.length - 1));
System.out.println("====================双向排序==================");
print(ARRAY2);
System.out.println("============================================");
print(sort(ARRAY2, 0, ARRAY2.length - 1));
}
}
时间复杂度
在拆分数组的时候可能会出现一种极端的情况,每次拆分的时候,基准数左边的元素个数都为0,而右边都为n-1个。这个时候,就需要拆分n次了。而每次拆分整理的时间复杂度为O(n),所以最坏的时间复杂度为O(n2)。什么意思?举个简单例子:
在不知道初始序列已经有序的情况下进行排序,第1趟排序经过n-1次比较后,将第1个元素仍然定在原来的位置上,并得到一个长度为n-1的子序列;第2趟排序经过n-2次比较后,将第2个元素确定在它原来的位置上,又得到一个长度为n-2的子序列;以此类推,最终总的比较次数:
C(n) = (n-1) + (n-2) + … + 1 = n(n-1)/2
所以最坏的情况下,快速排序的时间复杂度为O(n^2)
而最好的情况就是每次拆分都能够从数组的中间拆分,这样拆分logn次就行了,此时的时间复杂度为O(nlogn)。
而平均时间复杂度,则是假设每次基准数随机,最后算出来的时间复杂度为O(nlogn)
参考:快速排序的时间复杂度与空间复杂度
算法稳定性
通过上面的分析可以知道,在随机取基准数的时候,数据是可能会发生变化的,所以快速排序有不是稳定的情况。
总结
本篇文章就到这里了,希望能给你带来帮助,也希望您能够多多关注的更多内容!
加载全部内容