python实现CTC python实现CTC以及案例讲解

在大多数语音识别任务中，我们都缺少文本和音频特征的alignment，Connectionist Temporal Classification作为一个损失函数，用于在序列数据上进行监督式学习，可以不需要对齐输入数据及标签。

对于输入序列 X = [ x 1 , x 2 , . . , x T ] X=[x_1, x_2, .., x_T] X=[x1​,x2​,..,xT​] 和 输出序列 Y = [ y 1 , y 2 , . . . , y U ] Y = [y_1, y_2, ..., y_U ] Y=[y1​,y2​,...,yU​]，我们希望训练一个模型使条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X) 达到最大化，并且给定新的输入序列时我们希望模型可以推测出最优的输出序列， Y ∗ = a r g m a x Y   P ( Y ∣ X ) Y^*=\underset{Y}{argmax}\space P(Y|X) Y∗=Yargmax​ P(Y∣X)，而CTC算法刚好可以同时做到训练和解码。

损失函数

语音识别任务中，大多数情况下都是输入序列长度大于文本序列长度，所以CTC算法的alignment方案也是基于将连续的几帧输入合并对应到某一个输出的token，即多对一，同时除了训练数据中所有的token集合，CTC还引入了一个空白token，在这里用 ϵ \epsilon ϵ 指代，他没有实际意义并且在最终输出序列中被移除，但这个token对生成alignment很有帮助。

CTC算法生成最终token输出序列步骤如下：
生成和输入序列长度相同的alignment → 合并相同token → 删除空白token → token序列

上面步骤准确来讲是解码的步骤，解码之前我们要训练模型，训练模型就需要损失函数，或者说需要一个被优化的目标函数：

以下图的普通RNN为例， p t ( a t ∣ X ) p_t(a_t|X) pt​(at​∣X) 是每一帧在token集合（含空白token）上的概率分布

通过每一帧的概率分布我们可以得到所有（有效）alignment的概率，最后所有alignment都可以对应到一个输出序列，进而也就得到所有输出序列的概率分布。我们找到所有能够合并到 label （Y）序列的 alignment，并将他们的概率分数相加，再取负对数就可以得到一对训练数据的Loss。

那么对于整个数据集，可以得到目标函数 ∑ ( X , Y ) ∈ 训 练 数 据 集 − l o g   P ( Y ∣ X ) \sum_{(X,Y)\in 训练数据集}-log\space P(Y|X) ∑(X,Y)∈训练数据集​−log P(Y∣X)，训练中需要将其最小化。

用暴力的方法找出所有alignment并对其概率求和效率很低，常用的算法是通过动态规划对alignment进行合并，准确来讲是一个动态规划+DFS的算法：

为了实现这个算法，先引入一个中间序列 Z = ( ϵ , y 1 , ϵ , y 2 . . . , ϵ , y U ) Z=(\epsilon,y_1,\epsilon,y_2...,\epsilon,y_U) Z=(ϵ,y1​,ϵ,y2​...,ϵ,yU​)，也就是在label序列的起始，中间和终止位置插入空白token，引入这个中间序列可以说是CTC算法的精髓之一，下面我们以简单的 Y = ( a , b ) Y=(a,b) Y=(a,b) 输出序列进行说明：

中间序列 Z = ( ϵ , a , ϵ , b , ϵ ) Z=(\epsilon,a,\epsilon,b,\epsilon) Z=(ϵ,a,ϵ,b,ϵ)，长度为 S S S

输入序列 X = ( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ) X=(x_1, x_2, x_3, x_4,x_5,x_6) X=(x1​,x2​,x3​,x4​,x5​,x6​)，长度为 T T T

递归参数 α s , t \alpha_{s,t} αs,t​ 到 t t t 时刻为止中间序列的子序列 Z 1 : s Z_{1:s} Z1:s​获得的概率分数，也就是在 t t t时刻走到中间序列第 s s s个token时的概率分数

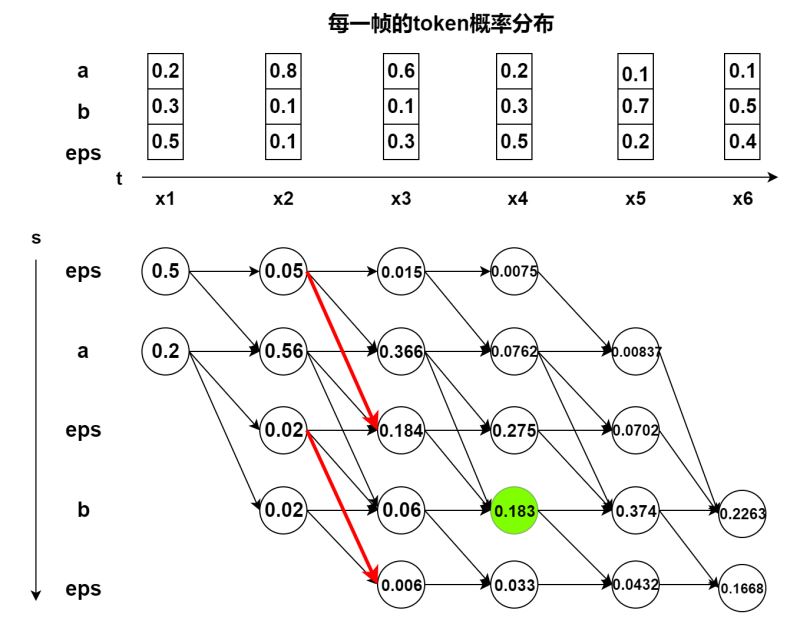
算法整体流程如下图所示，和原文中的图比起来加入了具体数值，理解起来更加直观，图中的红色路径表示不能进行跳转，因为如果直接从 t = 2 t=2 t=2 的第一个 ϵ \epsilon ϵ 跳到 t = 3 t=3 t=3 时刻的第3个 ϵ \epsilon ϵ，中间的token a a a 会被忽略，这样后面的路径不管怎么走都得不到正确的token序列。

其他情况下都可以接受来自上一个时刻的第 s − 2 , s − 1 , s s-2,s-1,s s−2,s−1,s个token的跳转，再对图中的节点做进一步解释，以绿色节点为例，该节点就是 α 4 , 4 \alpha_{4,4} α4,4​ （下标从1开始），表示前面不管怎么走，在 t = 4 t=4 t=4时刻落到第4个token时获得的概率分数，也就是把这个时刻能走到 b b b 的所有alignment 概率分数加起来。那么把最后一帧的2个节点的概率分数相加就是所有alignment的概率分数，即 P ( Y ∣ X ) = α S , T + α S − 1 , T P(Y|X)=\alpha_{S,T}+\alpha_{S-1, T} P(Y∣X)=αS,T​+αS−1,T​

下面直接给出dp的状态转换公式， p t ( z s ∣ X ) p_t(z_s|X) pt​(zs​∣X) 表示 t t t 时刻第 s s s 个字符的概率：

α s , t = ( α s , t − 1 + α s − 1 , t − 1 ) × p t ( z s ∣ X ) \alpha_{s,t}=(\alpha_{s,t-1}+\alpha_{s-1, t-1})\times p_t(z_s|X) αs,t​=(αs,t−1​+αs−1,t−1​)×pt​(zs​∣X)， ( a , ϵ , a ) (a,\epsilon, a) (a,ϵ,a)或者 ( ϵ , a , ϵ ) (\epsilon,a,\epsilon) (ϵ,a,ϵ) 模式

α s , t = ( α s − 2 , t − 1 + α s − 1 , t − 1 + α s , t − 1 ) × p t ( z s ∣ X ) \alpha_{s,t}=(\alpha_{s-2,t-1}+\alpha_{s-1,t-1}+\alpha_{s,t-1})\times p_t(z_s|X) αs,t​=(αs−2,t−1​+αs−1,t−1​+αs,t−1​)×pt​(zs​∣X)，其他情况

解码

解码问题就是已经有训练好的模型，需要通过输入序列推测出最优的token序列，实际上就是解决 Y ∗ = a r g m a x Y   P ( Y ∣ X ) Y^*=\underset{Y}{argmax}\space P(Y|X) Y∗=Yargmax​ P(Y∣X) 这个问题，那么能想到最直接的方法就是取每一帧概率分数最高的token，连接起来去掉 ϵ \epsilon ϵ 组成输出序列，也就是贪婪解码：

这样做虽然很高效但有时并不是最优解，比如几个概率分数较小的alignment序列最后都能转换为相同的token序列，那么将这些较小的alignment概率分数加起来可能会大于贪婪解码的概率分数。

常用的算法是改进版的beam search，常规的beam search是在每一帧都会保存概率分数最大的前几个路径并舍弃其他的，最后会给出最优的 b e a m beam beam 个路径，在此基础上，我们在路径搜索的过程中，需要对能映射到相同输出的alignment进行合并，合并之后再进行beam的枝剪。

和语言模型结合

CTC最明显的特点就是前后帧之间的条件独立假设

缺点：不适合包括语音识别在内的大多数seq2seq任务，上下文之间的相关性会被忽略，因此经常需要额外引入语言模型。

优点：不考虑上下文的相关性可以使模型泛化能力更强，比如如果不考虑文本之间的相关性，用于识别日常会话的声学模型可以直接用在会议内容转录的场景中。

由于语言模型分数和CTC的条件概率分数相互独立，因此最终的解码序列可以写成
Y ∗ = a r g m a x Y   P ( Y ∣ X ) × P ( Y ) α Y^*=\underset{Y}{argmax} \space P(Y|X)\times P(Y)^\alpha Y∗=Yargmax​ P(Y∣X)×P(Y)α， P ( Y ) P(Y) P(Y)表示语言模型的概率分数，可以是bigram也可以是3gram，以bigram为例的话，如果当前时刻序列是 ( a , b , c ) (a,b,c) (a,b,c)，计算下一帧跳到 d d d 的概率分数时，不仅要考虑下一时刻的token概率分布，还要考虑训练文本中 ( c , d ) (c,d) (c,d) 出现的频次，即 c o u n t ( c , d ) / c o u n t ( c , ∗ ) count(c,d) / count(c,*) count(c,d)/count(c,∗)，将这个概率和 d d d出现的概率相乘才是最终的概率分数， α \alpha α 是语言模型因子，需要fine tuning。

代码实现

损失函数（动态规划+DFS）
常规beam search解码
合并alignment的beam search解码
加入语言模型的 beam search解码