java动态规划 Java实现动态规划背包问题
Abro. 人气:0想了解Java实现动态规划背包问题的相关内容吗,Abro.在本文为您仔细讲解java动态规划的相关知识和一些Code实例,欢迎阅读和指正,我们先划重点:java动态规划,java动态规划背包,下面大家一起来学习吧。
前言
给定 n n n 种物品和一个背包。物品 i i i 的重量是 w i wi wi,其价值为 v i vi vi,背包的容量为 c c c。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
一、原理
0 − 0 - 0− 1 1 1 背包问题是一个特殊的整数规划问题。

1.1 最优子结构性质
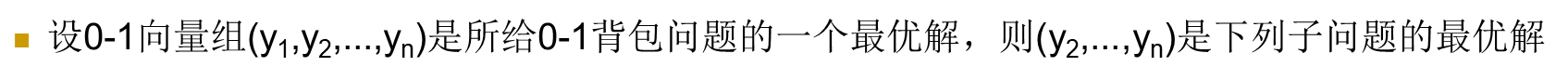
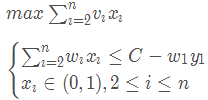
1.2 递归关系
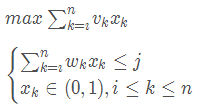
设所给 0 − 1 0-1 0−1 背包问题的子问题的最优值为 m(i,j),即 m(i,j)是背包容量为 j,可选择物品为 i,i+1,…,n 时 0-1背包问题的最优值。由 0-1背包问题的最优子结构性质,可以建立计算 m(i,j)的递归式如下:
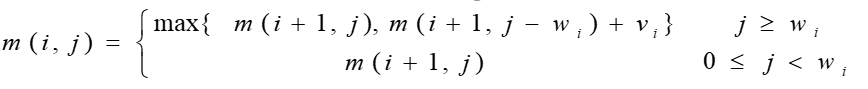
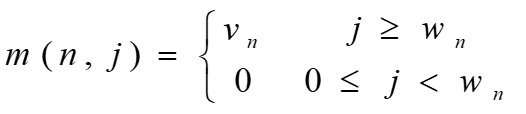
二、算法描述
2.1 算法描述
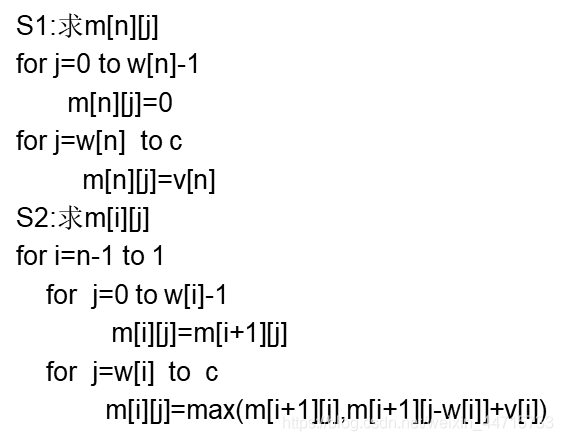
伪代码:

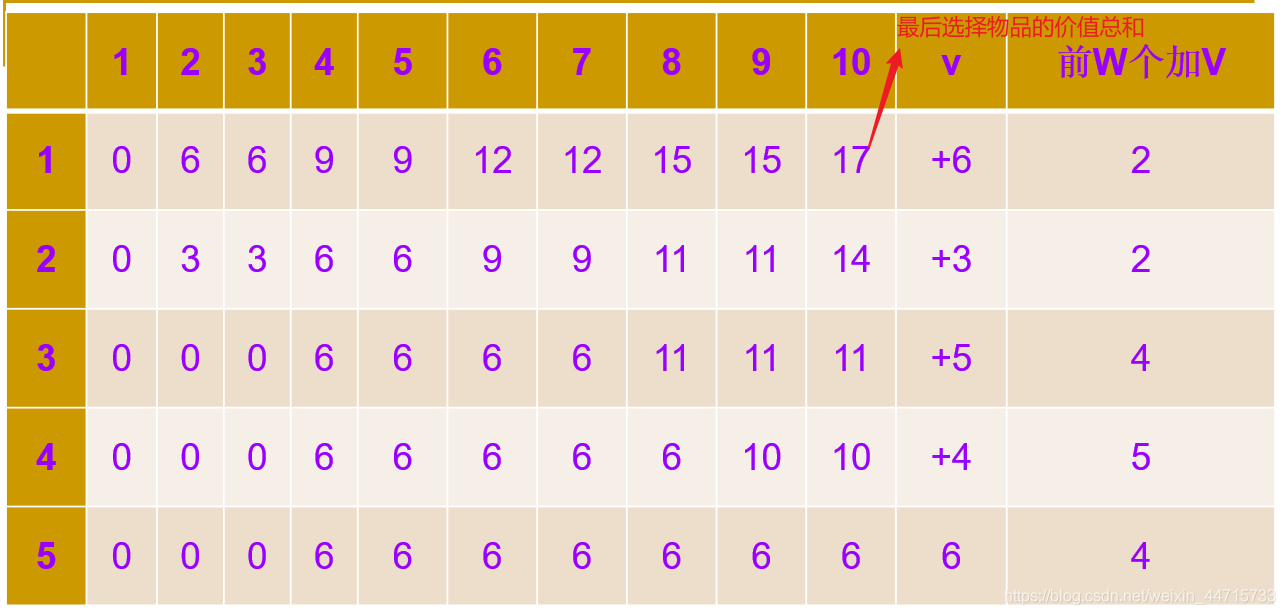
2.2 图解

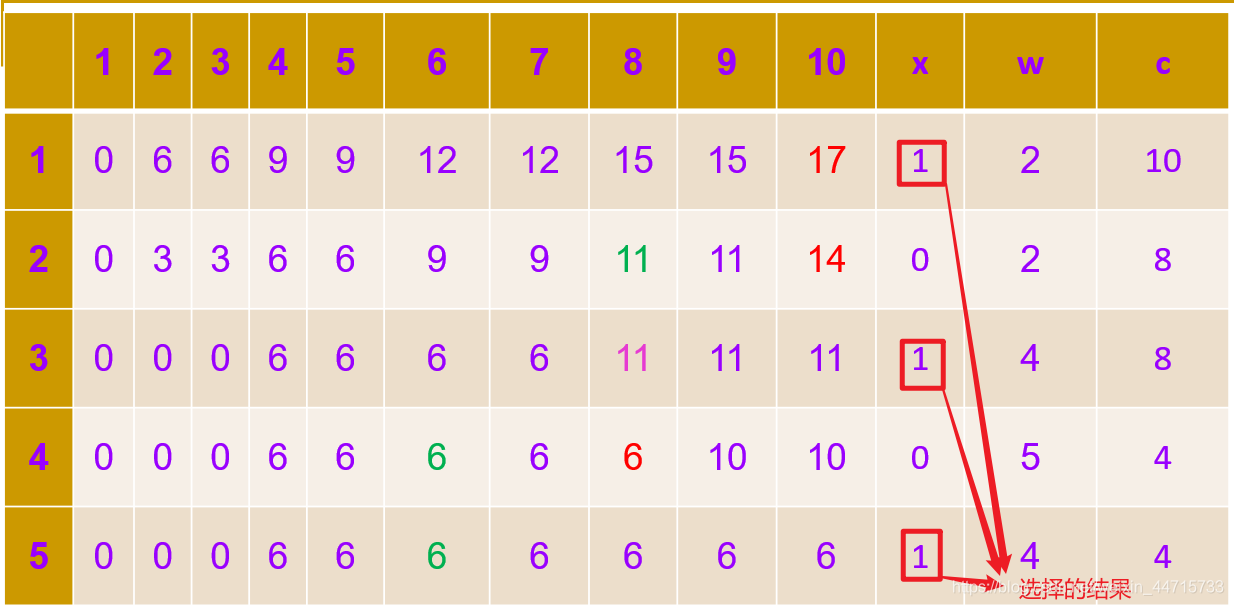
2.3 构造最优解

三、 0 − 1 0-1 0−1 背包问题相关题目
3.1 题目
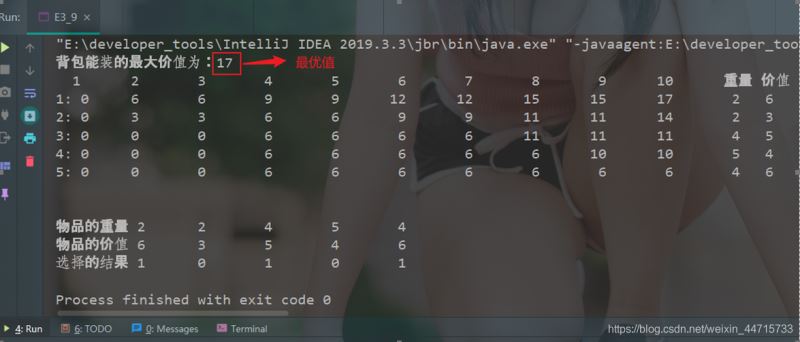
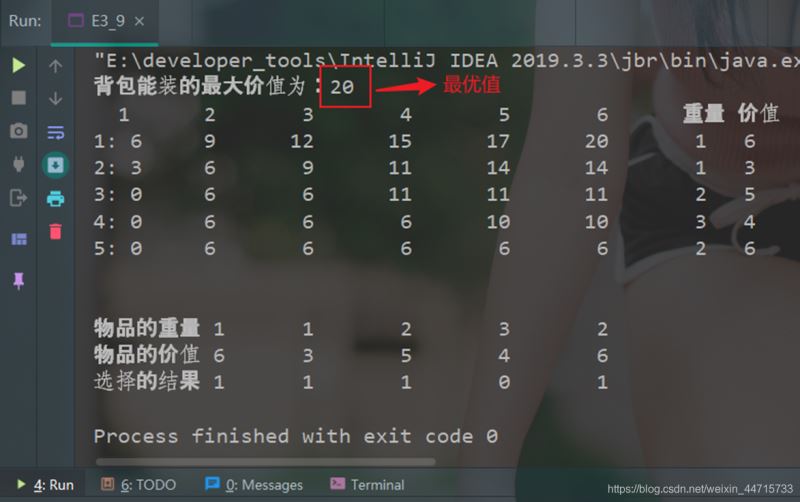
已知有5个物体,它们的重量分别为:2,2,4,5,4,各物体的价值依次为6,3,5,4,6,背包大小为10,使用动态规划法求矩阵m[i][j],并给出最优解。修改数据为:5个物体,它们的重量分别为:1,1,2,3,2,各物体的价值依次为6,3,5,4,6,背包大小为6,使用动态规划法求矩阵m[i][j],并给出最优解
3.2 源程序(Java求解 0 − 1 0-1 0−1背包问题)
/**
* 0-1背包问题(动态规划法求解)
*/
public class E3_9 {
//物品的个数+1(第一个数我写成0)
static int N = 6;
//static int C = 7;
static int C = 11;
/**
* 程序的入口
* @param args
*/
public static void main(String[] args) {
//int n = N-1;
//背包的容量
int c = C-1;
int i;
//物体的重量
//int w[] = new int[N];
int w[] = new int[]{0,2,2,4,5,4};
//int w[] = new int[]{0,1,1,2,3,2};
//物体的价值
//int v[] = new int[N];
int v[] = new int[]{0,6,3,5,4,6};
//动态规划法求解过程的矩阵
int m[][] = new int[N][C];
//选择的结果
int x[] = new int [N];
// for (i = 1; i < N; i++) {
// w[i] = 1+(int) (Math.random()*5);
// v[i] = 1+(int) (Math.random()*10);
// }
knapsack(v,w,c,m);
traceback(m,w,c,x);
System.out.printf("背包能装的最大价值为:"+"%d \n ",m[1][c]);
for (i = 1; i <= c; i++) {
System.out.printf("%2d \t",i);
}
System.out.printf("重量 价值\n");
for (i = 1; i < N; i++) {
System.out.printf("%d:",i);
for (int j = 1; j <= c; j++) {
System.out.printf("%2d \t",m[i][j]);
}
System.out.printf("%2d%4d\n",w[i],v[i]);
}
System.out.printf("\n\n物品的重量");
for (i = 1; i < N; i++) {
System.out.printf("%2d \t",w[i]);
}
System.out.printf("\n物品的价值");
for (i = 1; i < N; i++) {
System.out.printf("%2d \t",v[i]);
}
System.out.printf("\n选择的结果");
for (i = 1; i < N; i++) {
System.out.printf("%2d \t",x[i]);
}
System.out.printf("\n");
}
/**
* 由0-1背包问题的最优子结构性质建立的递归式
* @param v 存储物品价值的数组
* @param w 存储物品重量的数组
* @param c 背包容量
* @param m 动态规划法求解过程的矩阵
*/
public static void knapsack(int []v,int []w,int c,int [][]m){
int n=v.length-1;
int jMax=Math.min(w[n]-1,c);
for(int j=0;j<=jMax;j++) m[n][j]=0;
for(int j=w[n];j<=c;j++) m[n][j]=v[n];
for(int i=n-1;i>0;i--){
jMax=Math.min(w[i]-1,c);
for(int j=0;j<=jMax;j++)
m[i][j]=m[i+1][j];
for(int j=w[i];j<=c;j++)
m[i][j]=Math.max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
//m[1][c]=m[2][c];
//对于i=1时的两种情况
if(c>=w[1])
m[1][c]=Math.max(m[2][c],m[2][c-w[1]]+v[1]);
else
m[1][c]=m[2][c];
}
/**
* 构造最优解
* @param m 动态规划法求解过程的矩阵
* @param w 存储物体的重量的数组
* @param c 背包容量
* @param x 存储选择结果的数组
*/
public static void traceback(int [][]m,int []w,int c,int []x){
int n=w.length-1;
for(int i=1;i<n;i++)
if(m[i][c]==m[i+1][c])
x[i]=0;
else {
x[i]=1;
c-=w[i];
}
x[n]=(m[n][c]>0)?1:0;
}
}
3.3 运行结果
总结
动态规划基本步骤
- 找出最优解的性质,并刻划其结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解。
加载全部内容