Javascript结合Vue迷宫自动寻路 Javascript结合Vue实现对任意迷宫图片的自动寻路
最后的绅士 人气:0前言
可以直接体验最终效果:https://maze-vite.vercel.app/
寻路前:

寻路后,自动在图片上生成红色路径,蓝色是探索过的区域:

这里我故意用手机斜着角度拍,就是为了展示程序完全可以处理手机从现实拍摄的迷宫图片。
整个程序我准备用 Vue 3 + Vite 来写,但其实用不用 Vue 都一样,不会涉及复杂的界面,用别的框架甚至不用框架其实也完全可以。
二维数组,一本道
说了要从零开始,所以先尝试从非常简单的迷宫入手吧

对于我们人类来说,这个迷宫十分简单,显而易见的只有一条路。但是计算机解决这样的迷宫还是得稍微花费那么一点力气的。
二维数组很适合用来表达这个迷宫:
const m = [ [1, 1, 0, 0, 0], [0, 1, 1, 1, 0], [0, 0, 0, 1, 0], [0, 0, 0, 1, 1] ]
1 代表可以走的格子,0 代表不能走的格子。每个格子可以使用 [x, y] 来表示,比如这里起点是 [0, 0],终点是 [3, 4]。
那么应该有这么一个函数: function solveMaze (matrix, begin, end) {//...},matrix是描述迷宫的二维数组,begin 是起点,end 是终点,最终返回值是一个有序集合,每一个元素是一个格子,代表正确的路线轨迹。
这里我们准备采用的策略十分简单,从起点开始,看看周围上下左右(不能斜着走)哪些是可以走的格子,然后移动到这个格子,接着循环上面的步骤,直到遇到 end 格子,注意还需要记录上一步的格子,把它排除,以免走回头路。具体看以下代码:
// maze.js
function getPoint(m, x, y) {
if (x >= 0 && y >= 0 && x < m.length && y < m[x].length) {
return m[x][y]
} else {
return 0
}
}
function getNextPoint(m, current, lastPoint) {
let [x, y] = current
let nextPoint = [
[x - 1, y], [x + 1, y], [x, y - 1], [x, y + 1]
].find(p => {
let r1 = getPoint(m, p[0], p[1]) > 0
let r2 = !isSamePoint(p, lastPoint)
return r1 && r2
})
return nextPoint
}
function isSamePoint (p1, p2) {
return p1[0] === p2[0] && p1[1] === p2[1]
}
function solveMaze (matrix, begin, end) {
let path = []
// 当前点
let current = begin
path.push(current)
// 上次走过的路
let lastPoint = begin
// 随便挑一个可以走的点
while (1) {
if (isSamePoint(current, end)) {
break
}
let validPoint = getNextPoint(matrix, current, lastPoint)
path.push(validPoint)
lastPoint = current
current = validPoint
}
return path
}
const m = [
[1, 1, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 1]
]
console.log(
solveMaze(m, [0, 0], [3, 4])
)
getNextPoint 获取可以下一步通行的格子,solveMaze 获取最终可行走的路径,控制台输出:

这些坐标就是最终的行走轨迹,目测是正确的。
映射基础界面
为了方便测试观察,得把我们的数据结构映射到网页上面。
// maze.js
// ...
// 导出 solveMaze 函数,让vue组件调用
export {
solveMaze
}
<template>
<div>
<div class="div-matrix">
<div v-for="(row, x) in matrix" :key="x">
<div class="cell"
:class="{ black: p <= 0, path: isPath(x, y) }"
v-for="(p, y) in row" :key="y" :style="{ left: `${y * 2.5}em`, top: `${x * 2.5}em` }">
{{ begin[0] === x && begin[1] === y ? 'B' : '' }}
{{ end[0] === x && end[1] === y ? 'E' : '' }}
</div>
</div>
</div>
</div>
</template>
<script>
import { solveMaze } from './maze'
export default {
data () {
return {
begin: [0, 0],
end: [3, 4],
matrix: [],
paths: []
}
},
methods: {
isPath (x, y) {
const p = this.paths.find(path => path[0] === x && path[1] === y)
return p
}
},
created () {
const m = this.matrix = [
[1, 1, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 1]
]
this.paths = solveMaze(m, this.begin, this.end)
}
}
</script>
<style>
.top {
margin-bottom: 1em;
}
.div-matrix {
position: relative;
}
.cell {
border: 1px black solid;
width: 2em;
height: 2em;
position:absolute;
text-align: center;
}
.cell.path {
border: 1px red solid;
}
.black {
background: black;
}
</style>
最终效果:
其实就是通过二维数组 matrix 生成对应 div,数组里面元素值决定黑白。paths 数组存储结果路径,把路径用红色边框标记出来。这样就方便以后测试结果的查看了。
广度优先,地毯式搜索
看看下面这个迷宫:
const m = this.matrix = [ [1, 1, 0, 0, 0], [1, 1, 1, 1, 1], [0, 1, 0, 1, 0], [0, 1, 0, 1, 1] ]
如果把他应用到上面的代码,会发现页面卡死了,这是因为这个迷宫含有岔路,导致算法一直在绕圈。我们需要一些手段,把走过的路记住,以后就不再走了,方法不难,只要把当前可以走的格子,放进一个队列中,然后要做的,就是不断对这个队列里的格子,作出同样处理,直到遇到终点格子。
为了方便我们用算法进行处理,需要使用新的数据结构来表达,它就是 图(Graph) 结构。

图结构和链表很像,最大不同是每个节点可以有多个指针指向不同的节点。
同时把二维数组给他降维打击,变成一维:
const m = [ 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1 ]
虽然这样访问起来不那么直接,但是只需要一次寻址,复制传输也比二维数组方便得多。
然后创建一个 Node 类代表节点,NodeGraph 类代表整个图结构。
class Node {
constructor (x, y, value) {
this.x = x
this.y = y
this.value = value
this.checked = false
this.nearNodes = []
}
}
class NodeGraph {
constructor (matrix, width, height) {
this.nodes = []
this.matrix = matrix
this.width = width
this.height = height
}
buildNodeGraph () {
let { width, height } = this
for (let y = 0; y < height; y++) {
for (let x = 0; x < width; x++) {
let node = this.getNode(x, y)
let up = this.getNode(x, y - 1)
let down = this.getNode(x, y + 1)
let left = this.getNode(x - 1, y)
let right = this.getNode(x + 1, y)
node.nearNodes = [ up, down, left, right].filter(node => node && node.value === 1)
}
}
}
getNode (x, y) {
let { nodes, width, matrix } = this
if (x >= 0 && y >= 0) {
let node = nodes[y * width + x]
if (!node) {
let value = matrix[y * width + x]
if (value !== undefined) {
node = new Node(x, y, value)
nodes[y * width + x] = node
}
}
return node
} else {
return null
}
}
}
buildNodeGraph 把 matrix 数组转换为图结构,每个节点的 nearNodes 就相当于是下一步可以走的格子集合,checked 表示这个节点是否已经探索过。
为了方便查看每一步状态的变化,需要把当前所在格子和队列中的格子,在画面上标记出来,完整代码我就不贴了,codesandbox 可以随意看:
蓝色边框就是队列中的格子,小人就是当前所在的格子,当它走到右下角时就会停下来。
目前做的,只是顺利让小人移动到终点而已,但是怎么得出我们要的路径呢?方法就是在 Node 多加一个属性 parent,记录上一个 Node。当取出 nearNodes 时,把当前节点赋值到每一个 nearNode 的 parent 即可:
// ...
for (let node of current.nearNodes) {
if (node.checked === false) {
node.parent = current
queue.push(node)
}
}
// ...
然后就是从当前节点,读取 parent 一个一个回溯即可:
function buildPath (endNode) {
let path = []
let node = endNode
while (node) {
path.push(node)
node = node.parent
}
return path
}
效果:
当小人到达终点时,红色方格就是最短路径了。
地图编辑
稍微改动下代码,让我们可以实时编辑迷宫,测试更加方便。
操作:点击方格可以改变黑白状态,按住alt点击可以设置新的目标点。
逐渐把 solveMaze 里面的局部变量移到 NodeGraph 类里面,这样外部访问更加便利。注意当寻路结束的时候,不要结束函数,而是使用 while 循环一直等待新的目标点被设置:
// ...
if (equalsNode(current, nodeGraph.endNode)) {
while (equalsNode(current, nodeGraph.endNode)) {
await sleep(1000)
}
continue
}
// ...
优化寻路算法
想象一下这种情形:

起点和终点一条直线,中间毫无阻挡,但是这个小人竟然到处跑,好一会才到终点,这样下去不行的,必须要优化。
在 Node 类加一个属性 endDistance 记录每个节点到终点的距离,getDistance 函数根据坐标可以直接计算出距离,这个距离是没有考虑到中间可能出现的障碍的,但对路线的评估也十分有用:
class Node {
constructor (x, y, value) {
this.x = x
this.y = y
this.value = value
this.endDistance = 0 // 与终点的距离,忽略中间的障碍
this.checked = false
this.parent = null
this.nearNodes = []
}
}
function getDistance (nodeA, nodeB) {
const x = Math.abs(nodeB.x - nodeA.x)
const y = Math.abs(nodeB.y - nodeA.y)
return (x + y)
}
每次通过 popBestNextNode 方法从队列取出 endDistance 最小的 Node:
class NodeGraph {
// ...
popBestNextNode () {
let { queue } = this
let bestNode = queue[0]
let bestNodeIndex = 0
let { length } = queue
for (let i = 0; i < length; i++) {
let node = queue[i]
if (node.endDistance < bestNode.endDistance) {
bestNode = node
bestNodeIndex = i
}
}
queue.splice(bestNodeIndex, 1)
return bestNode
}
// ...
}
既然有 endDistance,那也要有 beginDistance,用来记录从起点走过来的步数。这个数值不直接从坐标计算,而是随着前进累加,这样 beginDistance 就不是估算值了,而是实际值:
// ...
for (let node of current.nearNodes) {
if (node.checked === false && node.value) {
node.parent = current
node.checked = true
node.endDistance = getDistance(node, nodeGraph.endNode)
node.beginDistance = current.beginDistance + 1
node.cost = node.endDistance + node.beginDistance
nodeGraph.queue.push(node)
}
}
// ...
考虑到以后可能会有新的因素加入,所以直接添加一个 cost 属性,用来表达 成本。目前 cost 就是 endDistance + beginDistance,cost 越小,优先级越高。

像这样的情况,小人一开始企图从上方靠近,但是随着不断前进,经过的步数越来越多,倒不如走下面了,于是就放弃的上面的路线。
现在,小人的行动变成更加靠谱了:
对图片进行寻路
拿这张我随便画的图来作为参数:
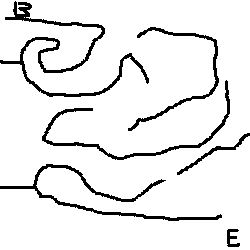
目标是从 B 点到达 E 点,我们只需要读取这张图片的像素,根据黑白颜色,转换成为一个数组,放到 solveMaze 函数即可。
为此,需要有一个 input 标签,type="file",用来选择图片,通过 URL.createObjectURL(File) 生成一个 URL,然后使用 new Image() 创建一个 img 标签,它不需要添加进 body,把 url 给到 img.src。通过 CanvasRenderingContext2D.drawImage() 复制进 Canvas,再调用 CanvasRenderingContext2D.getImageData() 即可获取像素数组。
这时不能再用 div 去渲染了,因为这张图几万个像素,每个像素一个 div 的话,浏览器也吃不消,再加上将来图片将会更大。
所以这里改用 Canvas 进行渲染,安排三个 Canvas,一个显示迷宫的原图,一个显示探索过的节点,一个显示当前最短路径,也就是 path 数组里面的节点,然后把这三个 Canvas 叠在一起即可,最后就是在回调里面去更新后面两个 Canvas 即可。
把我上面的图片下载到自己电脑,点击选择文件按钮选择图片,然后就能看到效果了,选别的图片也可以,只是我的起点和终点坐标是写死的,而且代码没有优化过,太大的图片恐怕难以处理。
注意:如果遇到跨域问题那就要自己上传图片了。
自定义起始点,以及随时变更路线
利用点击事件中的 offsetX、offsetY 即可知道点击坐标,把起点和终点的坐标保存起来,一旦有变化,则停止之前的寻路函数,重新执行当前的寻路函数,因此需要在循环中作一个判断来决定是否退出函数,这件事情适合在回调里面做。
然后提供一个输入框,自由调整经历多少个循环才更新一次画面,这样能调整寻路的速度。
处理彩色图片
预览:https://codesandbox.io/s/maze-vite-8-h845p?file=/src/App.vue (注意如果出现跨域错误,就自己上传图片吧)
不放iframe了,感觉放太多了,让这个页面已经相当卡。
前面都是默认白色像素是可以行走的区域,现在尝试把颜色相似的附近像素作为行走区域,这样效果会更加好。

直接把 rgba 颜色数据传入 solveMaze,然后在循环中计算出相邻节点与当前节点的颜色差距,差距过大则不放入队列。
把一个 rgba 整数的各个通道拆分开来可以这么写:
/**
* 获取 Node 的 RGB 值
* @param {Node} node
* @returns
*/
function getNodeRGB (node) {
let { value } = node
let r = value & 0xFF
let g = value >> 8 & 0xFF
let b = value >> 16 & 0xFF
return [ r, g, b ]
}
求 rgb 颜色的相似度,最朴素的方法是把两个颜色看成是两个三维坐标的点,然后求其欧几里得距离,但这不符合人眼的感知模型。详细方法wiki已经有了:https://zh.wikipedia.org/wiki/颜色差异
关于这方面的运算有点复杂,我都写到了 color.js 里面了。
结果:

注意代码里的 colorDiffThreshold,目前我用的 2.25,如果太高,会导致穿墙,太低则容易找不到路失败。
性能优化
当点击两次画面后,需要稍微等一会才会开始寻路,这里应该耗费了不少CPU。打开 DevTools 的性能分析器分析下到底是哪里消耗最多性能:

很明显 solveMaze 函数占据了大多数时间,展开下面的 Call Tree:

buildNodeGraph 和 getNode 是优化重点,打开代码,可以直接看到每句话耗费的CPU时间:

57 行的 if (!node) {...} 明明是简单的判断,却耗费了不少时间,试试看改成 node === undefined,并且 value 也不再需要判断了。对 nodes 数组的访问与读取也耗费不少时间,尝试一开始用 new Array(length) 初始化,应该会好一些。优化之后的代码:

看起来稍微好一些。
在寻路途中进行性能监测:
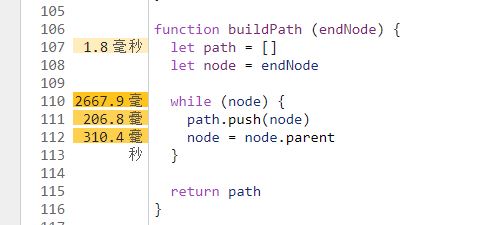
发现 buildPath 相当的耗费时间,这也是理所应当的,毕竟每次循环都调用,并且完整遍历整个链条。处理办法也简单,只在最后出结果时调用他即可,根据前面的经验,while (node) 改为 while (node !== null)。

现在他完全没有存在感了。
然后是 for...of 语句,建议改为传统的数组下标自减,这是最快的,当然日常使用 for...of 可读性更强。

然后是 popBestNextNode:
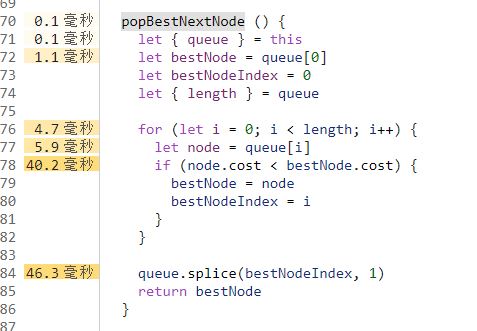
这里每次都完整遍历整个数组找出cost最小的节点,最后还有一个数组元素移除的操作。我真的很难判断 JavaScript 的数组到底是存储在连续内存里面还是分散的,但是不管怎么样,这里完全可以使用二叉堆替代来获取更好的性能。具体就不自己实现了,直接用现成的:https://www.npmjs.com/package/heap-js。注意 new Heap() 的时候传入自定义的比较器,然后把 popBestNextNode 的实现改为 return this.queue.pop() 即可。
最后,把 buildNodeGraph 的那两层for循环全部移除,不再预先初始化所有的 Node,给 NodeGraph 添加一个新方法:
getNearNodes (node) {
let { x, y } = node
let up = this.getNode(x, y - 1)
let down = this.getNode(x, y + 1)
let left = this.getNode(x - 1, y)
let right = this.getNode(x + 1, y)
return [ up, down, left, right ].filter(node => node !== null)
}
在后面的寻路循环中再去调用 getNearNodes 来获取相邻的节点,这样就大幅缩减了一开始的卡顿了。
最后,提供两种策略:
- 严格:当相邻像素颜色差距小于某个值,才加入队列。适合行走区域的颜色变化不大的图片,得出的结果几乎就是最短的路径。
- 模糊:相邻像素无论颜色的差距,都加入队列,其差距值乘以某些系数,作为节点的 cost。适合任何图片,最终总是能找到一条路。。。
let nearNodes = nodeGraph.getNearNodes(current)
for (let i = nearNodes.length - 1; i >= 0; i--) {
let node = nearNodes[i]
if (node.checked === false) {
node.checked = true
let colordiff = getNodeColorDiff(node, current)
const colorDiffThreshold = 2 // 容许通过的颜色差异,范围 0~100
node.parent = current
node.endDistance = getDistance(node, nodeGraph.endNode)
node.beginDistance = current.beginDistance + 1
if (mode === "1") { // 严格
node.cost = node.endDistance + node.beginDistance
if (colordiff < colorDiffThreshold) {
nodeGraph.queue.push(node)
}
} else if (mode === "2") { // 模糊
node.cost = node.endDistance + node.beginDistance + (colordiff * width * height)
nodeGraph.queue.push(node)
}
}
}
加载全部内容