亲宝软件园·资讯

展开

opencv图像矫正 深入讨论opencv图像矫正算法实战

唯有自己强大 人气:0
想了解深入讨论opencv图像矫正算法实战的相关内容吗，唯有自己强大在本文为您仔细讲解opencv图像矫正的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：opencv图像矫正,opencv图像校正，下面大家一起来学习吧。

摘要

在机器视觉中，对于图像的处理有时候因为放置的原因导致ROI区域倾斜，这个时候我们会想办法把它纠正为正确的角度视角来，方便下一步的布局分析与文字识别，这个时候通过透视变换就可以取得比较好的裁剪效果。

本次实战，对于图像的矫正使用了两种矫正思路：

基于轮廓提取的矫正算法

整体思路：

opencv实现（分解步骤）：

（一）图片灰度化，二值化（开运算，消除噪点）

  Mat src = imread("D:/opencv练习图片/图片矫正.png");
    imshow("原图片", src);
    // 二值图像
    Mat gray, binary;
    cvtColor(src, gray, COLOR_BGR2GRAY);
    threshold(gray, binary, 0, 255, THRESH_BINARY_INV| THRESH_OTSU);
    imshow("二值化", binary);
    // 定义结构元素
    Mat se = getStructuringElement(MORPH_RECT, Size(3, 3), Point(-1, -1));
    morphologyEx(binary, binary, MORPH_OPEN, se);
    imshow("开运算", binary);

注意：由于原图像背景是白色，因此二值化时候要用THRESH_BINARY_INV

（二）提取轮廓，筛选轮廓

// 寻找最大轮廓
    vector<vector<Point>> contours;
    findContours(binary, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
    int index = -1;
    int max = 0;
    for (size_t i = 0; i < contours.size(); i++) 
    {
        double area = contourArea(contours[i]);
        if (area > max) 
        {
            max = area;
            index = i;
        }
    }

（三）求取最小外接矩形以及四顶点坐标，并定义变换后的四顶点坐标

// 寻找最小外接矩形
    RotatedRect rect = minAreaRect(contours[index]);    
    Point2f srcpoint[4];//存放变换前四顶点
    Point2f dstpoint[4];//存放变换后四顶点
    rect.points(srcpoint);//获取最小外接矩形四顶点坐标
    //显示顶点
    for (size_t i = 0; i < 4; i++)
    {
        circle(src, srcpoint[i], 5, Scalar(0, 0, 255),-1);//-1表示填充
    }
    imshow("顶点坐标", src);
    //获取外接矩形宽高
    float width = rect.size.width;
    float height = rect.size.height;
    //定义矫正后四顶点
    dstpoint[0]= Point2f(0, height);
    dstpoint[1] = Point2f(0, 0);
    dstpoint[2] = Point2f(width, 0);
    dstpoint[3] = Point2f(width, height);

😄 这里需要注意的是：

RotatedRect 类的矩形返回的是矩形的中心坐标，倾斜角度。

Rect类的矩形返回的是矩形的左上角坐标，宽，高。因此要获取RotatedRect 类的矩形的宽，高就要用：

//获取外接矩形宽高
    float width = rect.size.width;
    float height = rect.size.height;

获取RotatedRect 类四顶点坐标的顺序依次是：左下-左上-右上-右下（可通过显示顶点依次查看）

对应矫正后的四顶点就是：(0，height)-(0，0)-(width，0)-(width，height）

（四）透视变换

// 透视变换
    Mat M = getPerspectiveTransform(srcpoint, dstpoint);
    Mat result = Mat::zeros(Size(width, height), CV_8UC3);
    warpPerspective(src, result, M, result.size());
    imshow("矫正结果", result);

基于霍夫直线探测的矫正算法

对于文本图像（如图），它没有明显的轮廓边缘去求四顶点。但是经过深入分析，可以发现：文本的每一行文字都是呈一条直线，而且这些直线都是平行的！

利用这个特征就可以实现基于霍夫直线探测的矫正算法：

用霍夫线变换探测出图像中的所有直线计算出每条直线的倾斜角，求他们的平均值根据倾斜角旋转矫正

💙先来看看什么是霍夫变换：

霍夫变换在检测各种形状的的技术中非常流行，如果你要检测的形状可以用数学表达式写出，你就可以是使用霍夫变换检测它。

霍夫变换的直线检测简单来说就是在空间坐标系和映射到另外一个参数空间，将空间坐标系中的每一个点映射到另外一个参数空间中的线，通过该参数空间中所有线的交叉次数得到实际空间坐标系中的直线。

在OpenCV中，使用Hough变换的直线检测在函数HoughLines和HoughLinesP中实现。

HoughLines函数（标准霍夫变换）

从平面坐标转换到霍夫空间，最终输出是找到直线的极坐标（r，θ）

HoughLines(
InputArray src,        // 输入图像，必须CV_8U的二值图像（常用canny处理后的二值图像）
OutputArray lines,     // 输出的极坐标来表示直线
double rho,            // 步长(常为1）
double theta,          //角度，（一般是CV_PI/180）
int threshold,         // 阈值，只有获得足够交点的极坐标点才被看成是直线
double min_theta=0，   // 表示角度扫描范围 0 ~180之间， 默认即可
double max_theta=CV_PI) 
// 一般情况是有经验的开发者使用，需要自己反变换到平面空间

HoughLinesP函数（霍夫变换直线概率)

从平面坐标转换到霍夫空间，最终输出是找到直线的起点和终点（直角坐标系）

HoughLinesP(
InputArray src, // 输入图像，必须CV_8U的二值图像
OutputArray lines, // 输出找到直线的两点
double rho, // 步长（半径，常设为1）
double theta, //角度，一般取值CV_PI/180
Int threshold, // 阈值，累计次数必须达到的值,一般为150
double minLineLength=0，// 最小直线长度，一般为50
double maxLineGap=0）// 最大间隔，一般为10

opencv实现（分解步骤）：

（一）图片灰度化，Canny边缘提取

Mat src, src_edge, src_gray,src_rotate;
    double angle;
    src = imread("D:/opencv练习图片/文本矫正.png");
    imshow("文本图片", src);
    cvtColor(src, src_gray, COLOR_RGB2GRAY);
    Canny(src_gray, src_edge, 50, 200, 3);
    imshow("canny", src_edge);

（二） 霍夫直线检测（HoughLines函数）并显示

//通过霍夫变换检测直线
    vector<Vec2f> plines;
    //第5个参数就是阈值，阈值越大，检测精度越高
    HoughLines(src_edge, plines, 1, CV_PI / 180, 200, 0, 0);
    cout << plines.size() << endl;
    //由于图像不同，阈值不好设定，因为阈值设定过高导致无法检测直线，阈值过低直线太多，速度很慢
    //所以根据阈值由大到小设置了三个阈值，如果经过大量试验后，可以固定一个适合的阈值。
    
    float sum = 0;
    //依次画出每条线段
    for (size_t i = 0; i < plines.size(); i++)
    {
        float rho = plines[i][0];
        float theta = plines[i][1];
        Point pt1, pt2;
        double a = cos(theta), b = sin(theta);
        double x0 = a * rho, y0 = b * rho;
        pt1.x = cvRound(x0 + 1000 * (-b));//cvRound四舍五入
        pt1.y = cvRound(y0 + 1000 * (a));
        pt2.x = cvRound(x0 - 1000 * (-b));
        pt2.y = cvRound(y0 - 1000 * (a));
        sum += theta;
        line(src_gray, pt1, pt2, Scalar(55, 100, 195), 1, LINE_AA);//Scalar函数用于调节线段颜色         
        imshow("直线探测效果图", src_gray);
        float average = sum / plines.size(); //对所有角度求平均，这样做旋转效果会更好
        angle = DegreeTrans(average) - 90;
    }

😊核心代码分析：

由于需要求解直线的倾斜角度，因此这里使用了HoughLines函数，返回的是直线的步长和弧度（极坐标系下）

通过极坐标系下的步长和弧度，可以转换到直接坐标系下的两点坐标，然后显示。（原理如图）

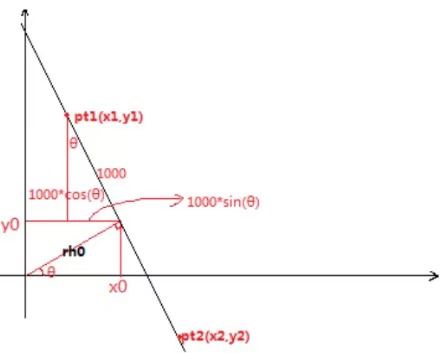
（三）根据倾斜角度，进行放射变换（逆时针旋转矫正）

    //旋转中心为图像中心    
    Point2f center;
    center.x = float(src.cols / 2.0);
    center.y = float(src.rows / 2.0);
    int length = 0;
    length = sqrt(src.cols*src.cols + src.rows*src.rows);
    Mat M = getRotationMatrix2D(center, angle, 1);
    warpAffine(src, src_rotate, M, Size(length, length), 1, 0, Scalar(255, 255, 255));//仿射变换，背景色填充为白色  
    imshow("矫正后", src_rotate);

加载全部内容
相关教程
猜你喜欢
用户评论