Java哈夫曼树 Java数据结构之哈夫曼树概述及实现

时间:2021-05-13 菜菜的大数据开发の路人气:0

想了解Java数据结构之哈夫曼树概述及实现的相关内容吗，菜菜的大数据开发の路在本文为您仔细讲解Java哈夫曼树的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：Java哈夫曼树,Java数据结构,java树，下面大家一起来学习吧。

一、与哈夫曼树相关的概念

概念	含义
1. 路径	从树中一个结点到另一个结点的分支所构成的路线
2. 路径长度	路径上的分支数目
3. 树的路径长度	长度从根到每个结点的路径长度之和
4. 带权路径长度	结点具有权值, 从该结点到根之间的路径长度乘以结点的权值, 就是该结点的带权路径长度
5. 树的带权路径长度	树中所有叶子结点的带权路径长度之和

二、什么是哈夫曼树

定义:

给定n个权值作为n个叶子结点, 构造出的一棵带权路径长度(WPL)最短的二叉树,叫哈夫曼树(), 也被称为最最优二叉树.
WPL: Weighted Path Length of Tree 树的带权路径长度

哈夫曼树的特点:

1.权值越大的结点, 距离根节点越近;

2.树中没有度为1的结点, 哈夫曼树的度只能是0 或 1;

3.带权路径长度最短的一棵二叉树;

判断下图三个二叉树那个是哈夫曼树?

当然是WPL最小的树啦, 即中间的二叉树是也;

那么我们是如何手动构造出一棵哈夫曼树的呢?

三、哈夫曼树的构造方法

构造哈夫曼树的步骤:

1.把所有结点的权值按照从小到大的顺序进行排序;

2.取出根节点权值最小的两棵二叉树;

3.组成一棵新的二叉树, 这课新二叉树的根节点的权值是前面两棵二叉树权值的和

4.再将这棵新的二叉树,以根节点的权值大小进行排序, 不断重复1-2-3-4的步骤, 直到给定序列中的所有权值都被处理,我们就得到了一棵哈夫曼树.

[图解分析构造过程]

下面以序列{13,7,8,3}为例, 图解构造哈夫曼树的过程

首先对序列进行升序排列,得到{3,7,8,13};

取出权值最小的两个结点3,7 , 组成一棵二叉树,根节点是权值为10的结点;

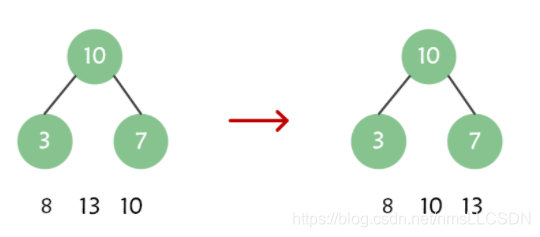
在原序列中去除步骤2中已经被使用了的3和7, 并把新的结点权值10加入到序列中并重新排序, 得到{8,10,13};

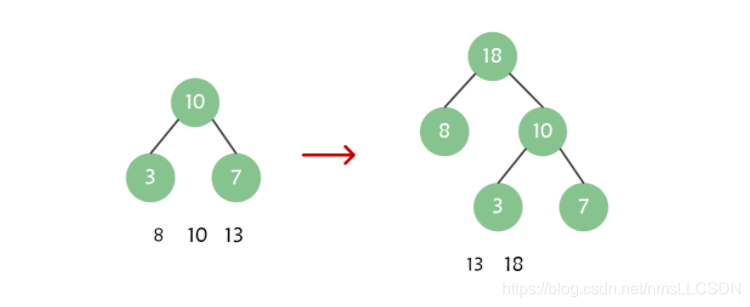
再次取出权值最小的两个节点8,10, 组成一棵根节点为18的二叉树, 然后我们去除序列中的8,10, 将18添加到序列中并排序, 得到了{13,18};

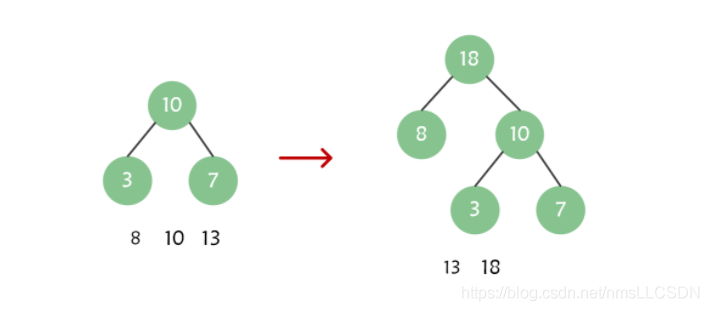
将序列{13,18}取出构成一棵新的二叉树, 权值为31, 此时序列中只剩下了31这个结点, 他是这个哈夫曼树的根节点;

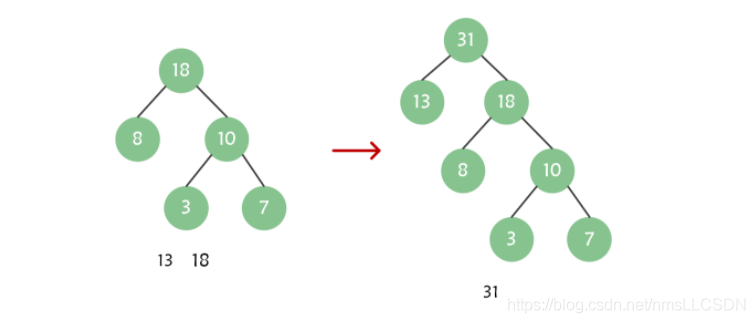
至此, {13,7,8,3}的哈夫曼树构建完毕.

四、哈夫曼树的代码实现

结点类

package DataStrcture.huffmantreedemo;

public class HTreeNode implements Comparable<HTreeNode>{
    //
    public HTreeNode leftNode;
    public HTreeNode rightNode;
    public int weight;

    // 前序遍历
    public void preOrder(){

        System.out.println(this);

        if(this.leftNode != null) this.leftNode.preOrder();

        if(this.rightNode != null) this.rightNode.preOrder();
    }

    // 设置左右子节点
    public void setLeftNode(HTreeNode node){
        this.leftNode = node;
    }
    public void setRightNode(HTreeNode node){
        this.rightNode = node;
    }
    //构造方法和toString()
    public HTreeNode(int weight){
        this.weight = weight;
    }
    public String toString(){
        return "Node{weight: "+weight+"}";
    }
    //根据权值对结点进行排序
//    public int compareTo(Object obj){
//        return this.weight - ((HTreeNode)(obj)).weight;
//    }
    public int compareTo(HTreeNode node){
        return this.weight - node.weight;
    }
}

哈夫曼树类

package DataStrcture.huffmantreedemo;

import java.util.ArrayList;
import java.util.Collections;

public class HuffmanTree{
    //哈夫曼树的实现:
    //1. 构建哈夫曼树的方法 buildHuffumanTree(int[] arr)
    //2. 对哈夫曼树进行遍历(二叉树遍历)
    public static void main(String[] args) {
        int[] arr = {13,7,8,3,29,6,1};
        HTreeNode hTreeNode = buildHuffmanTree(arr);
        preOrder(hTreeNode);
    }
    public static HTreeNode buildHuffmanTree(int[] arr){
        //
        ArrayList<HTreeNode> nodesList = new ArrayList<HTreeNode>();
        //1. 把存放权值的数组拿出来构建结点
        //2. 把这些节点存放到集合中
        for(int x : arr){
            nodesList.add(new HTreeNode(x));
        }
        while(nodesList.size() > 1){
            //3. 利用集合的排序方法,可以根据权值对结点进行排序
            Collections.sort(nodesList);
            // (当然了, 我们需要实现comparable接口中的copareTo方法), 在哪实现的? 在结点类中!
            //4. 不断的循环从集合中取出两个结点进行相加, 直到集合中只剩下一个结点才会终止循环
            HTreeNode leftNode = nodesList.get(0);
            HTreeNode rightNode = nodesList.get(1);

            HTreeNode parent = new HTreeNode(leftNode.weight + rightNode.weight);
            建立父节点和左右子节点的关系(千万不要忘了)
            //因为我们虽说是父节点和左右子节点, 还是要实实在在的于内存中体现出来的哈
            parent.setLeftNode(leftNode);
            parent.setRightNode(rightNode);
            //5.从结合中移除用过的左右子节点, 添加父节点进去
            nodesList.remove(leftNode);
            nodesList.remove(rightNode);
            nodesList.add(parent);
        }
        //6. 返回一个最终的唯一结点
        return nodesList.get(0);
    }
    //前序遍历哈夫曼树
    public static void preOrder(HTreeNode root){
        if(root != null){
            root.preOrder();
        }else{
            System.out.println("二叉树为空! ");
        }
    }
}

加载全部内容