pytorch autograde计算图 pytorch-autograde-计算图的特点说明

在PyTorch实现中，autograd会随着用户的操作，记录生成当前variable的所有操作，并由此建立一个有向无环图。用户每进行一个操作，相应的计算图就会发生改变。

更底层的实现中，图中记录了操作Function，每一个变量在图中的位置可通过其grad_fn属性在图中的位置推测得到。在反向传播过程中，autograd沿着这个图从当前变量（根节点\textbf{z}z）溯源，可以利用链式求导法则计算所有叶子节点的梯度。

每一个前向传播操作的函数都有与之对应的反向传播函数用来计算输入的各个variable的梯度，这些函数的函数名通常以Backward结尾。

下面结合代码学习autograd的实现细节。

在PyTorch中计算图的特点可总结如下：

autograd根据用户对variable的操作构建其计算图。对变量的操作抽象为Function

对于那些不是任何函数(Function)的输出，由用户创建的节点称为叶子节点，叶子节点的grad_fn为None。叶子节点中需要求导的variable，具有AccumulateGrad标识，因其梯度是累加的

variable默认是不需要求导的，即requires_grad属性默认为False，如果某一个节点requires_grad被设置为True，那么所有依赖它的节点requires_grad都为True

variable的volatile属性默认为False，如果某一个variable的volatile属性被设为True，那么所有依赖它的节点volatile属性都为True。volatile属性为True的节点不会求导，volatile的优先级比requires_grad高。

多次反向传播时，梯度是累加的。反向传播的中间缓存会被清空，为进行多次反向传播需指定retain_graph=True来保存这些缓存

非叶子节点的梯度计算完之后即被清空，可以使用autograd.grad或hook技术获取非叶子节点的值

variable的grad与data形状一致，应避免直接修改variable.data，因为对data的直接操作无法利用autograd进行反向传播

反向传播函数backward的参数grad_variables可以看成链式求导的中间结果，如果是标量，可以省略，默认为1

PyTorch采用动态图设计，可以很方便地查看中间层的输出，动态的设计计算图结构

在 e.backward() 执行求导时，系统遍历 e.grad_fn.next_functions ，分别执行求导。

如果 e.grad_fn.next_functions 中有哪个是 AccumulateGrad ，则把结果保存到 AccumulateGrad 的variable引用的变量中。

否则，递归遍历这个function的 next_functions ，执行求导过程。

最终到达所有的叶节点，求导结束。同时，所有的叶节点的 grad 变量都得到了相应的更新。

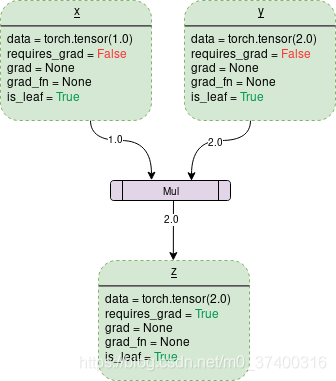
他们之间的关系如下图所示：

例子：

x = torch.randn(5, 5)
y = torch.randn(5, 5)
z = torch.randn((5, 5), requires_grad=True)
a = x + z
print(a.requires_grad)

可以z是一个标量，当调用它的backward方法后会根据链式法则自动计算出叶子节点的梯度值。

但是如果遇到z是一个向量或者是一个矩阵的情况，这个时候又该怎么计算梯度呢？这种情况我们需要定义grad_tensor来计算矩阵的梯度。在介绍为什么使用之前我们先看一下源代码中backward的接口是如何定义的：

torch.autograd.backward(
		tensors, 
		grad_tensors=None, 
		retain_graph=None, 
		create_graph=False, 
		grad_variables=None)

grad_tensors作用

x = torch.ones(2,requires_grad=True)
z = x + 2
z.backward()
>>> ...
RuntimeError: grad can be implicitly created only for scalar outputs

当我们运行上面的代码的话会报错，报错信息为RuntimeError: grad can be implicitly created only for scalar outputs。

x = torch.ones(2,requires_grad=True)
z = x + 2
z.sum().backward()
print(x.grad)
>>> tensor([1., 1.])

我们再仔细想想，对z求和不就是等价于z点乘一个一样维度的全为1的矩阵吗？即sum(Z)=dot(Z,I),而这个I也就是我们需要传入的grad_tensors参数。(点乘只是相对于一维向量而言的，对于矩阵或更高为的张量，可以看做是对每一个维度做点乘)

代码如下：

x = torch.ones(2,requires_grad=True)
z = x + 2
z.backward(torch.ones_like(z)) # grad_tensors需要与输入tensor大小一致
print(x.grad)
>>> tensor([1., 1.])

x = torch.tensor([2., 1.], requires_grad=True).view(1, 2)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)
z = torch.mm(x, y)
print(f"z:{z}")
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")
>>> z:tensor([[5., 8.]], grad_fn=<MmBackward>)
x.grad: tensor([[1., 3.]])
y.grad: tensor([[2., 0.],
        [1., 0.]])

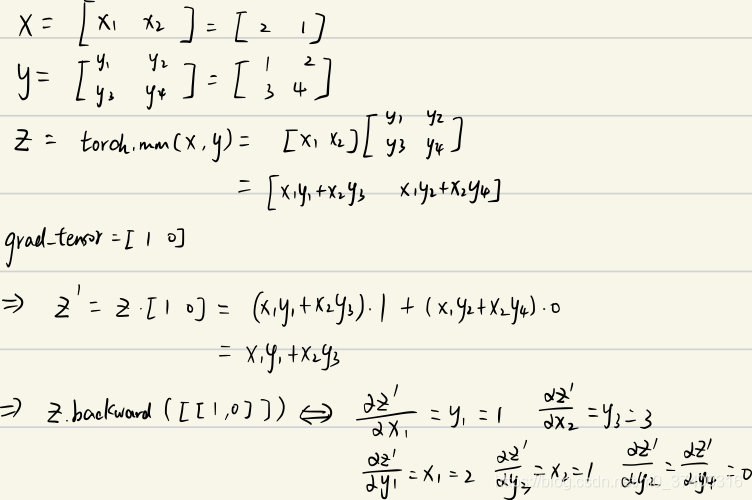
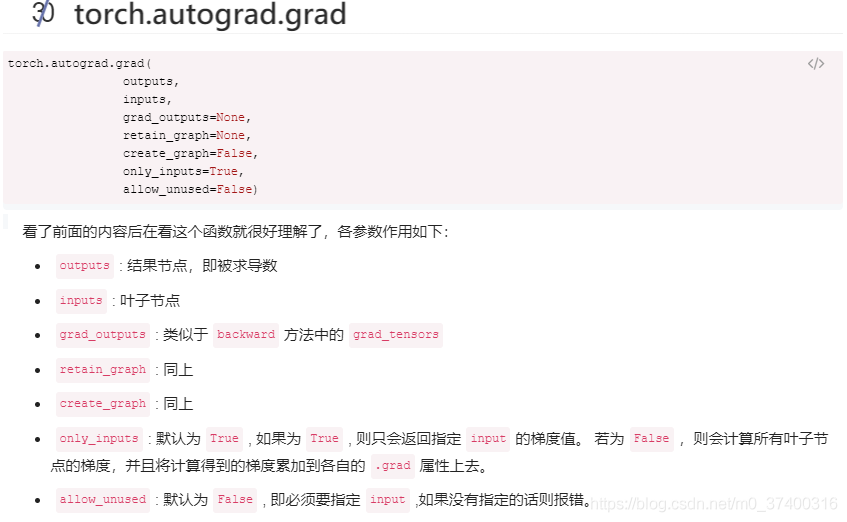
补充：PyTorch的计算图和自动求导机制

自动求导机制简介

PyTorch会根据计算过程自动生成动态图，然后根据动态图的创建过程进行反向传播，计算每个节点的梯度值。

为了能够记录张量的梯度，首先需要在创建张量的时候设置一个参数requires_grad=True，意味着这个张量将会加入到计算图中，作为计算图的叶子节点参与计算，最后输出根节点。

对于PyTorch来说，每个张量都有一个grad_fn方法，包含创建该张量的运算的导数信息。在反向传播的过程中，通过传入后一层的神经网络的梯度，该函数会计算出参与运算的所有张量的梯度。

同时，PyTorch提供了一个专门用来做自动求导的包torch.autograd。它包含两个重要的函数，即torch.autograd.bakward和torch.autograd.grad。

torch.autograd.bakward通过传入根节点的张量以及初始梯度张量，可以计算产生该根节点的所有对应叶子节点的梯度。当张量为标量张量时，可以不传入梯度张量，这是默认会设置初始梯度张量为1.当计算梯度张量时，原先建立起来的计算图会被自动释放，如果需要再次做自动求导，因为计算图已经不存在，就会报错。如果要在反向传播的时候保留计算图，可以设置retain_graph=True。

另外，在自动求导的时候默认不会建立反向传播的计算图，如果需要在反向传播的计算的同时建立梯度张量的计算图，可以设置create_graph=True。对于一个可求导的张量来说，也可以调用该张量内部的backward方法。

自动求导机制实例

定义一个函数f(x)=x2，则它的导数f'(x)=2x。于是可以创建一个可导的张量来测试具体的导数。

t1 = torch.randn(3, 3, requires_grad=True) # 定义一个3×3的张量
print(t1)
t2 = t1.pow(2).sum() # 计算张量的所有分量的平方和
t2.backward() # 反向传播
print(t1.grad) # 梯度是原始分量的2倍
t2 = t1.pow(2).sum() # 再次计算张量的所有分量的平方和
t2.backward() # 再次反向传播
print(t1.grad) # 梯度累积
print(t1.grad.zero_()) # 单个张量清零梯度的方法

得到的结果：

tensor([[-1.8170, -1.4907,  0.4560],
        [ 0.9244,  0.0798, -1.2246],
        [ 1.7800,  0.0367, -2.5998]], requires_grad=True)
tensor([[-3.6340, -2.9814,  0.9120],
        [ 1.8488,  0.1597, -2.4492],
        [ 3.5600,  0.0735, -5.1996]])
tensor([[ -7.2681,  -5.9628,   1.8239],
        [  3.6975,   0.3193,  -4.8983],
        [  7.1201,   0.1469, -10.3992]])
tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])

需要注意的一点是： 张量绑定的梯度张量在不清空的情况下会逐渐累积。这在例如一次性求很多Mini-batch的累积梯度时是有用的，但在一般情况下，需要注意将张量的梯度清零。

梯度函数的使用

如果不需要求出当前张量对所有产生该张量的叶子节点的梯度，可以使用torch.autograd.grad函数。

这个函数的参数是两个张量，第一个张量是计算图的张量列表，第二个参数是需要对计算图求导的张量。最后输出的结果是第一个张量对第二个张量求导的结果。

这个函数不会改变叶子节点的grad属性，同样该函数在反向传播求导的时候释放计算图，如果要保留计算图需要设置retain_graph=True。

另外有时候会碰到一种情况：求到的两个张量之间在计算图上没有关联。在这种情况下需要设置allow_unused=True，结果会返回分量全为0的梯度张量。

t1 = torch.randn(3, 3, requires_grad=True)
print(t1)
t2 = t1.pow(2).sum() 
print(torch.autograd.grad(t2, t1)) 

得到的结果为：

tensor([[ 0.5952,  0.1209,  0.5190],
        [ 0.4602, -0.6943, -0.7853],
        [-0.1460, -0.1406, -0.7081]], requires_grad=True)
(tensor([[ 1.1904,  0.2418,  1.0379],
        [ 0.9204, -1.3885, -1.5706],
        [-0.2919, -0.2812, -1.4161]])

计算图构建的启用和禁用

由于计算图的构建需要消耗内存和计算资源，在一些情况下计算图并不是必要的，所以可以使用torch.no_grad这个上下文管理器，对该管理器作用域中的神经网络计算不构建任何的计算图。

还有一种情况是对于一个张量，在反向传播的时候可能不需要让梯度通过这个张量的节点，也就是新建的计算图需要和原来的计算图分离，使用张量的detach方法，可以返回一个新的张量，该张量会成为一个新的计算图的叶子结点。

总结

PyTorch使用动态计算图，该计算图的特点是灵活。虽然在构件计算图的时候有性能开销，但PyTorch本身的优化抵消了一部分开销，尽可能让计算图的构建和释放过程代价最小，因此，相对于静态图的框架来说，PyTorch本身的运算速度并不慢。

有了计算图之后，就可以很方便地通过自动微分机制进行反向传播的计算，从而获得计算图叶子节点的梯度。在训练深度学习模型的时候，可以通过对损失函数的反向传播，计算所有参数的梯度，随后在优化器中优化这些梯度。

以上为个人经验，希望能给大家一个参考，也希望大家多多支持。