python sympy常微分方程 python中sympy库求常微分方程的用法
t4ngw 人气:0问题1:
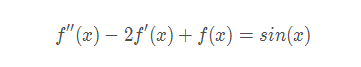
程序,如下
from sympy import *
f = symbols('f', cls=Function)
x = symbols('x')
eq = Eq(f(x).diff(x, x) - 2*f(x).diff(x) + f(x), sin(x))
print(dsolve(eq, f(x)))
结果
Eq(f(x), (C1 + C2*x)*exp(x) + cos(x)/2)
1.利用python的Sympy库求解微分方程的解

程序,如下
from sympy import *
f = symbols('f', cls=Function)
x = symbols('x')
eq = Eq(f(x).diff(x,1)+f(x)+f(x)**2, 0)
print(dsolve(eq, f(x)))
C1 = symbols('C1')
eqr = -C1/(C1 - exp(x))
eqr1 = eqr.subs(x, 0)
print(solveset(eqr1 - 1, C1))
eqr2 = eqr.subs(C1, 1/2)
# 画图
import matplotlib.pyplot as plt
import numpy as np
x_1 = np.arange(-5, 5, 0.1)
y_1 = [-0.5/(0.5 - exp(x)) for x in x_1]
plt.plot(x_1, y_1)
plt.axis([-6,6,-10,10])
plt.grid()
plt.show()
结果
Eq(f(x), -C1/(C1 - exp(x)))
FiniteSet(1/2)

2.利用python的Sympy库求解微分方程的解
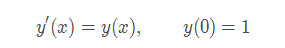
程序,如下
from sympy import *
y = symbols('y', cls=Function)
x = symbols('x')
eq = Eq(y(x).diff(x,1), y(x))
print(dsolve(eq, y(x)))
C1 = symbols('C1')
eqr = C1*exp(x)
eqr1 = eqr.subs(x, 0)
print(solveset(eqr1 - 1, C1))
eqr2 = eqr.subs(C1, 1)
# 画图
import matplotlib.pyplot as plt
import numpy as np
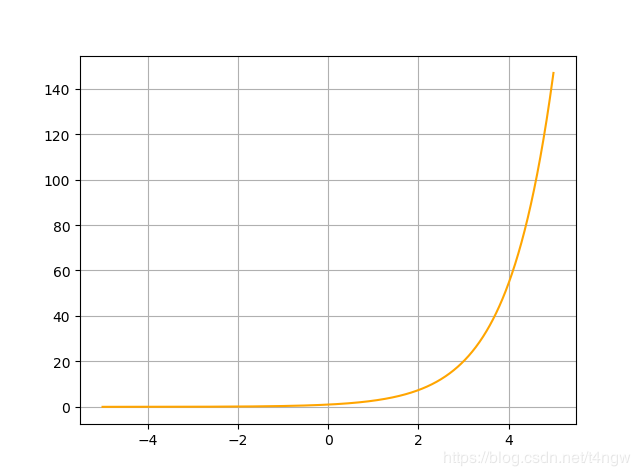
x_1 = np.arange(-5, 5, 0.01)
y_1 = [exp(x) for x in x_1]
plt.plot(x_1, y_1, color='orange')
plt.grid()
plt.show()
结果
Eq(y(x), C1*exp(x))
FiniteSet(1)
加载全部内容