python平稳时间序列建模 利用python实现平稳时间序列的建模方式
Nicole_Liang 人气:4一、平稳序列建模步骤
假如某个观察值序列通过序列预处理可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列进行建模。建模的基本步骤如下:
(1)求出该观察值序列的样本自相关系数(ACF)和样本偏自相关系数(PACF)的值。
(2)根据样本自相关系数和偏自相关系数的性质,选择适当的ARMA(p,q)模型进行拟合。
(3)估计模型中位置参数的值。
(4)检验模型的有效性。如果模型不通过检验,转向步骤(2),重新选择模型再拟合。
(5)模型优化。如果拟合模型通过检验,仍然转向不走(2),充分考虑各种情况,建立多个拟合模型,从所有通过检验的拟合模型中选择最优模型。
(6)利用拟合模型,预测序列的将来走势。
二、代码实现
1、绘制时序图,查看数据的大概分布
trainSeting.head() Out[36]: date 2017-10-01 126.4 2017-10-02 82.4 2017-10-03 78.1 2017-10-04 51.1 2017-10-05 90.9 Name: sales, dtype: float64 plt.plot(trainSeting)

2、平稳性检验
'''进行ADF检验
adf_test的返回值
Test statistic:代表检验统计量
p-value:代表p值检验的概率
Lags used:使用的滞后k,autolag=AIC时会自动选择滞后
Number of Observations Used:样本数量
Critical Value(5%) : 显著性水平为5%的临界值。
(1)假设是存在单位根,即不平稳;
(2)显著性水平,1%:严格拒绝原假设;5%:拒绝原假设,10%类推。
(3)看P值和显著性水平a的大小,p值越小,小于显著性水平的话,就拒绝原假设,认为序列是平稳的;大于的话,不能拒绝,认为是不平稳的
(4)看检验统计量和临界值,检验统计量小于临界值的话,就拒绝原假设,认为序列是平稳的;大于的话,不能拒绝,认为是不平稳的
'''
#滚动统计
def rolling_statistics(timeseries):
#Determing rolling statistics
rolmean = pd.rolling_mean(timeseries, window=12)
rolstd = pd.rolling_std(timeseries, window=12)
#Plot rolling statistics:
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
##ADF检验
from statsmodels.tsa.stattools import adfuller
def adf_test(timeseries):
rolling_statistics(timeseries)#绘图
print ('Results of Augment Dickey-Fuller Test:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value #增加后面的显著性水平的临界值
print (dfoutput)
adf_test(trainSeting) #从结果中可以看到p值为0.1097>0.1,不能拒绝H0,认为该序列不是平稳序列
返回结果如下

Results of Augment Dickey-Fuller Test: Test Statistic -5.718539e+00 p-value 7.028398e-07 #Lags Used 0.000000e+00 Number of Observations Used 6.200000e+01 Critical Value (1%) -3.540523e+00 Critical Value (5%) -2.909427e+00 Critical Value (10%) -2.592314e+00 dtype: float64
通过上面可以看到,p值小于0.05,可以认为该序列为平稳时间序列。
3、白噪声检验
'''acorr_ljungbox(x, lags=None, boxpierce=False)函数检验无自相关 lags为延迟期数,如果为整数,则是包含在内的延迟期数,如果是一个列表或数组,那么所有时滞都包含在列表中最大的时滞中 boxpierce为True时表示除开返回LB统计量还会返回Box和Pierce的Q统计量 返回值: lbvalue:测试的统计量 pvalue:基于卡方分布的p统计量 bpvalue:((optionsal), float or array) – test statistic for Box-Pierce test bppvalue:((optional), float or array) – p-value based for Box-Pierce test on chi-square distribution ''' from statsmodels.stats.diagnostic import acorr_ljungbox def test_stochastic(ts,lag): p_value = acorr_ljungbox(ts, lags=lag) #lags可自定义 return p_value
test_stochastic(trainSeting,[6,12])
Out[62]: (array([13.28395274, 14.89281684]), array([0.03874194, 0.24735042]))
从上面的分析结果中可以看到,延迟6阶的p值为0.03<0.05,因此可以拒绝原假设,认为该序列不是白噪声序列。
4、确定ARMA的阶数
(1)利用自相关图和偏自相关图
####自相关图ACF和偏相关图PACF import statsmodels.api as sm def acf_pacf_plot(ts_log_diff): sm.graphics.tsa.plot_acf(ts_log_diff,lags=40) #ARIMA,q sm.graphics.tsa.plot_pacf(ts_log_diff,lags=40) #ARIMA,p acf_pacf_plot(trainSeting) #查看数据的自相关图和偏自相关图
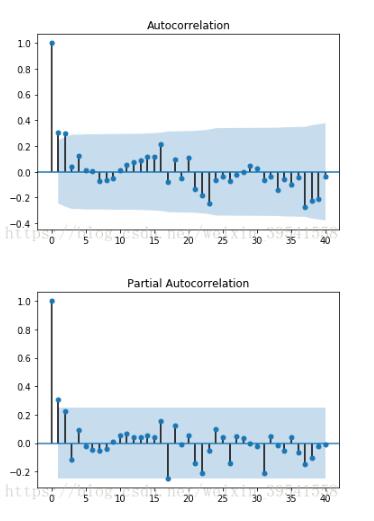
(2)借助AIC、BIC统计量自动确定
##借助AIC、BIC统计量自动确定
from statsmodels.tsa.arima_model import ARMA
def proper_model(data_ts, maxLag):
init_bic = float("inf")
init_p = 0
init_q = 0
init_properModel = None
for p in np.arange(maxLag):
for q in np.arange(maxLag):
model = ARMA(data_ts, order=(p, q))
try:
results_ARMA = model.fit(disp=-1, method='css')
except:
continue
bic = results_ARMA.bic
if bic < init_bic:
init_p = p
init_q = q
init_properModel = results_ARMA
init_bic = bic
return init_bic, init_p, init_q, init_properModel
proper_model(trainSeting,40)
#在statsmodels包里还有更直接的函数: import statsmodels.tsa.stattools as st order = st.arma_order_select_ic(ts_log_diff2,max_ar=5,max_ma=5,ic=['aic', 'bic', 'hqic']) order.bic_min_order ''' 我们常用的是AIC准则,AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个模型。 为了控制计算量,我们限制AR最大阶不超过5,MA最大阶不超过5。 但是这样带来的坏处是可能为局部最优。 timeseries是待输入的时间序列,是pandas.Series类型,max_ar、max_ma是p、q值的最大备选值。 order.bic_min_order返回以BIC准则确定的阶数,是一个tuple类型
返回值如下:
order.bic_min_order
Out[13]: (1, 0)
5、建模
从上述结果中可以看到,可以选择AR(1)模型
################################模型######################################
# AR模型,q=0
#RSS是残差平方和
# disp为-1代表不输出收敛过程的信息,True代表输出
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(trainSeting,order=(1,0,0)) #第二个参数代表使用了二阶差分
results_AR = model.fit(disp=-1)
plt.plot(trainSeting)
plt.plot(results_AR.fittedvalues, color='red') #红色线代表预测值
plt.title('RSS:%.4f' % sum((results_AR.fittedvalues-trainSeting)**2))#残差平方和

6、预测未来走势
############################预测未来走势########################################## # forecast方法会自动进行差分还原,当然仅限于支持的1阶和2阶差分 forecast_n = 12 #预测未来12个天走势 forecast_AR = results_AR.forecast(forecast_n) forecast_AR = forecast_AR[0] print (forecast_AR)
print (forecast_ARIMA_log)
[90.49452199 84.05407353 81.92752342 81.22536496 80.99352161 80.9169700380.89169372 80.88334782 80.88059211 80.87968222 80.87938178 80.87928258]
##将预测的数据和原来的数据绘制在一起,为了实现这一目的,我们需要增加数据索引,使用开源库arrow:
import arrow
def get_date_range(start, limit, level='day',format='YYYY-MM-DD'):
start = arrow.get(start, format)
result=(list(map(lambda dt: dt.format(format) , arrow.Arrow.range(level, start,limit=limit))))
dateparse2 = lambda dates:pd.datetime.strptime(dates,'%Y-%m-%d')
return map(dateparse2, result)
# 预测从2017-12-03开始,也就是我们训练数据最后一个数据的后一个日期
new_index = get_date_range('2017-12-03', forecast_n)
forecast_ARIMA_log = pd.Series(forecast_AR, copy=True, index=new_index)
print (forecast_ARIMA_log.head())
##绘图如下
plt.plot(trainSeting,label='Original',color='blue')
plt.plot(forecast_ARIMA_log, label='Forcast',color='red')
plt.legend(loc='best')
plt.title('forecast')
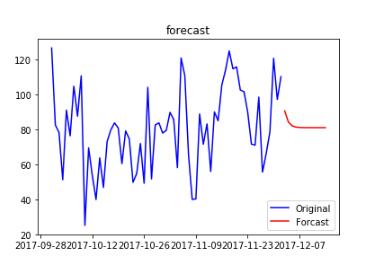
以上这篇利用python实现平稳时间序列的建模方式就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持。
加载全部内容