C语言二叉搜索树 C语言实现二叉搜索树的完整总结
奋斗的龙猫 人气:01、 二叉树的构建
我们都知道二叉搜索树的特点是:当前节点的值大于它的左子树的值,小于等于右子树的值。所以我们这里可以通过迭代的方式构建二叉搜索树,当然也可以通过递归的方式构建二叉树。
定义一个结构体,表示节点:
typedef struct NODE{
int va;
struct NODE *left,*right;
}Node;
①通过迭代的方式实现二叉搜索树的构建,值得注意的是,这种方式构建二叉搜索树的时候,需要定义一个变量,表示这个节点插入的位置是父节点的左子节点还是右子节点的位置,同时定义一个变量,表示插入的父节点。
Node * createBinaryTree(Node *root,int val){
int isLeftChild = 0;//定义一个临时变量,表示这个新节点的插入位置是否为它的左子节点
Node *cur = root,*parent = NULL,*node;
node = (Node *)malloc(sizeof(Node));
if(node == NULL){
printf("创建节点失败!!!\n");
exit(0);//退出虚拟机
}
node->val = val;
node->left = node->right = NULL;
while(*cur != NULL){
//找到新节点要插入的位置
parent = cur;
if(cur->val > x){
cur = cur->left;//新节点的值小于当前节点的值,那么就往当前节点的左子树方向进行查找
isLeftChild = 1;
} else{
cur = cur->right;//如果新节点的值大于等于当前节点的值,那么就往当前节点的右子树方向进行查找
isLeftChild = 0;
}
}
//判断parent/root是否为空,如果为空,说明新节点是根节点
if(pre == NULL){
root = node;
}else{
//parent不为空,说明不是空树,这是需要判断插入的位置是否是在左子节点的位置
if(isLeftChild){
parent->left = node;
}else{
parent->right= node;
}
}
return root;
}
②通过迭代的方式进行创建二叉搜索树
Node *createBinaryTree(Node *root,int val){
if(root == NULL){
root = (Node *)malloc(sizeof(Node));//给新节点分配空间
if(root == NULL){
printf("创建节点失败!!!\n"):
exit(0);//退出虚拟机
}
root->val = val;
root->left = root->right = NULL;
}else{
//如果当前的节点不为空,那么就判断新节点插入的是左子节点还是右子节点的位置
if(val < root->val)//新节点的值小于当前节点的值,说明将其插入在当前节点左子树的位置
root->left = createBinaryTree(root->left,val);
else//新节点的值大于等于当前节点的值,说明时将其插入在当前节点的右子树位置
root->right = createBinaryTree(root->right,val);
}
return root;
}
2、二叉树的遍历
二叉树的遍历主要包括几种遍历方式,分别是前序遍历,中序遍历,后序遍历,层序遍历。
前序遍历:先访问当前的节点,然后访问它的左子树,最后访问它的右子树。
中序遍历:先访问当前节点的左子树,然后访问自身,最后访问它的右子树。
后序遍历:先访问当前节点的左子树,然后访问当前节点的右子树,最后才访问自身。
层序遍历:一层一层,从左到右遍历的。
前序遍历
递归实现
void preOrderDisplay(Node *root){
if(root != NULL){
printf("%5d",root->val);//访问自身
preOrderDisplay(root->left);//访问当前节点的左子树
preOrderDisplay(root->right);//访问当前节点的右子树
}
}
迭代实现
注意的是,通过迭代实现二叉树的前序遍历,我们需要利用到栈。
void preOrderTraversal(Node *root){
Stack *s;
if(!createStack(s)){
printf("创建栈失败!!!\n");
return;
}
Node *t = root,k;
while(t != NULL || !isEmpty(s)){
//当前的节点不为空,或者栈不为空,那么就继续进循环
while(t!= NULL){
//如果当前的节点不为空,那么就将当前的节点输出,然后将它的左子树压入栈中(遍历到最左)
printf("%5d",t->val);//由于是前序遍历,那么先输出父节点的值
pushStack(s,t);
t = t->left;
}
if(!isEmpty(s)){
//如果栈不为空,那么这时候,将从栈中跳出一个节点,并且将获得它的右子树,然后将右子树压入栈中
popStack(s,k);//(跳出一个节点)
t = k.right;//将右子树重复上面的操作(往这个跳出节点k的右子树方向移动)
}
}
}
中序遍历
递归实现
//利用递归中序遍历树
void InOrderDisplay(Node *root){
if(root != NULL){
//如果节点不为空,那么递归实现中序遍历
InOrderDisplay(root->left);//先访问左子树
printf("%5d",root->val);//访问自身
InOrderDisplay(root->right);//访问右子树
}
}
迭代实现
/*
利用迭代循环实现树的中序遍历
基本思路:利用堆栈实现的
基本步骤:
1、判断当前的节点或者栈是否为空,如果其中至少有一个不为空,那么
这时候将进入循环
2、判断当前的节点是否为空,(必须要判断,因为进入外部循环的循环条件有两个,所以不知道是否因为当前
节点是否为空),如果节点不为空,那么将当前的节点压入栈中,然后当前的节点变成它的左节点,将它的左子树压入
栈中
3、判断栈是否为空,将栈顶节点跳出,并将其输出,然后后去这个跳出节点的右子节点
*/
void InOrderTraversal(Node *root){
Stack *s;
Node *t = root,k;
if(!createStack(s)){
printf("创建栈失败!!!\n");
return;
}
while(t != NULL || !isEmpty(s)){
while(t != NULL){
pushStack(s,t);//将当前的节点及其左子树压入栈中(遍历到最左)
t = t->left;
}
if(!isEmpty(s)){
//从栈中跳出最后一个左子节点的父节点
popStack(s,k);
printf("%5d",k.val);//输入当前节点的值
t = k.right;//将其右子树压入栈中(往跳出节点k的右子树方向移动)
}
}
}
后序遍历
递归实现
/*
递归实现树的后序遍历
*/
void postOrderDisplay(Node *root){
if(root != NULL){
//当前的节点不为空,那么就先访问左子树,然后访问右子树,最后访问当前的节点
postOrderDisplay(root->left);
postOrderDisplay(root->right);
printf("%5d",root->val);
}
}
迭代实现
/*
利用迭代实现树的后序遍历:
基本思路:
1、判断当前的节点或者栈是否为空,如果其中至少有一个不为空,那么循环继续
2、判断该当前的节点是否为空,如果不为空,那么就将当前的节点及其左子树压入栈中
3、判断当前的栈是否为空,如果不为空,那么就从栈中跳出一个节点
获取这个节点的右子节点,如果这个右子节点为空,那么就将当前的节点输出,然后再吃从栈中跳出一个节点
4、重复上面的2、3步骤
*/
void postOrderTraversal(Node *root){
Node *t = root,k,pre;//pre表示上一次访问过的右子节点
Stack *s;
if(!createStack(s)){
printf("创建栈失败!!!\n");
return;
}
while(t != NULL || !isEmpty(s)){
//如果当前的节点不为空或者栈不为空,那么就继续循环遍历
while(t != NULL){
//如果当前的节点不为空,那么就将其压入栈中
pushStack(s,t);
t = t->left;
}
//注意这里并不是直接从栈中跳出一个节点,而是先获取栈顶节点,判断条件满足之后才跳出节点
if( getTop(s,k) && k.right == NULL || pre.val == k.right->val){
/*
判断当前的栈顶节点的右子节点是否为空,或者这个栈顶的右子节点已经输
出过了,如果这个栈顶节点的右子节点为空或者已经输出过了,那么就将这
个栈顶节点从栈中跳出,并输出它的值否则,就将这个栈顶节点的右子树压
入栈中,重复循环操作
*/
popStack(s,k);
pre = k;
printf("%5d",k.val);
}else{
t = k.right;//如果上面的条件不满足,那么就往它的右子树方向移动
}
}
}
测试完整代码:
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 100
#define INCREMENT 10
#define ERROR 0
#define OK 1
typedef struct NODE{
int val;
struct NODE *left;
struct NODE *right;
}Node;
typedef struct STACK{
Node * arr;
int top;
}Stack;
//创建栈
int createStack(Stack *s){
s->arr = (Node *)malloc(sizeof(Node) * MAX_SIZE);//分配MAX_SIZE个空间
if(s->arr == NULL)
//如果arr为空,说明分配空间事变,这时候返回ERROR
return ERROR;
s->top = 0;
return OK;
}
//压栈
int pushStack(Stack *s,Node *node){
if(s->top == MAX_SIZE){
return ERROR;
}
Node t;
t.val = node->val;
t.left = node->left;
t.right = node->right;
s->arr[s->top++] = t;
return OK;
}
//出栈
int popStack(Stack *s,Node &node){
if(s->top == 0){
//如果栈为空,那么这时候返回ERROR
return ERROR;
}
node = s->arr[--s->top];//获取栈顶节点
return OK;
}
int getTop(Stack *s,Node &k){
if(s->top == 0)
return ERROR;
k = s->arr[s->top - 1];
return OK;
}
//判断栈是否为空
int isEmpty(Stack *s){
return s->top == 0;
}
/*
节点的插入基本思路:
判断这颗树是否为空树,如果是一棵空树,那么新节点就是整棵树的
根节点,如果不是,那么就需要通过遍历找到插入的位置。
根据二叉搜索树的特点,如果新节点的值小于根节点或者父节点的值,那么就
往左边走,找到第一个为空的地方,然后将其插入;如果新节点的值大于等于父节点的值,
那么就往右边走,找到第一个为空的地方,将其插入。
值得注意的是,我们需要标记插入的是否为左子节点还是右子节点,所以需要定义一个临时
变量,判断插入的位置是否为父节点的左节点
*/
Node * insert(Node *root,int val){
Node *node = (Node *)malloc(sizeof(Node));
node->val = val;
node->left = NULL;
node->right = NULL;
//如果不是空树,那么就需要定义临时变量,表示插入的位置是否为左节点
//同时定义一个临时节点,表示要插入位置的父节点
Node *current = root,*parent = NULL;
int isLeftChild = 1; //值为1表示插入的是父节点的左子节点的位置,否则为右子节点的位置
while(current != NULL){
parent = current;//表示插入位置的父节点
if(current->val > val){
//如果当前的节点比新节点的值大,那么就往左子节点的方向走
isLeftChild = 1;
current = current->left;
}else{
isLeftChild = 0;
current = current->right;
}
}
if(parent == NULL){
//如果parent为空,说明是一棵空树,此时新节点就是根节点
root = node;
}else{
if(isLeftChild)
parent->left = node;
else
parent->right = node;
}
return root;
}
//利用递归中序遍历树
void InOrderDisplay(Node *root){
if(root != NULL){
//如果节点不为空,那么递归实现中序遍历
InOrderDisplay(root->left);//先访问左子树
printf("%5d",root->val);//访问自身
InOrderDisplay(root->right);//访问右子树
}
}
void preOrderDisplay(Node *root){
if(root != NULL){
//如果root节点不为空,那么就进行递归
printf("%5d",root->val);
preOrderDisplay(root->left);//访问左子树
preOrderDisplay(root->right);//访问右子树
}
}
/*
递归实现树的后序遍历
*/
void postOrderDisplay(Node *root){
if(root != NULL){
//当前的节点不为空,那么就先访问左子树,然后访问右子树,最后访问当前的节点
postOrderDisplay(root->left);
postOrderDisplay(root->right);
printf("%5d",root->val);
}
}
/*
利用迭代实现树的后序遍历:
基本思路:
1、判断当前的节点或者栈是否为空,如果其中至少有一个不为空,那么循环继续
2、判断该当前的节点是否为空,如果不为空,那么就将当前的节点及其左子树压入栈中
3、判断当前的栈是否为空,如果不为空,那么就从栈中跳出一个节点
获取这个节点的右子节点,如果这个右子节点为空,那么就将当前的节点输出,然后再吃从栈中跳出一个节点
4、重复上面的2、3步骤
*/
void postOrderTraversal(Node *root){
Node *t = root,k,pre;//pre表示上一次访问过的右子节点
Stack *s;
if(!createStack(s)){
printf("创建栈失败!!!\n");
return;
}
while(t != NULL || !isEmpty(s)){
//如果当前的节点不为空或者栈不为空,那么就继续循环遍历
while(t != NULL){
//如果当前的节点不为空,那么就将其压入栈中
pushStack(s,t);
t = t->left;
}
//注意这里并不是从栈中跳出一个节点
if( getTop(s,k) && k.right == NULL || pre.val == k.right->val){
/*
判断当前的栈顶节点的右子节点是否为空,或者这个栈顶的右子节点已经输出过了
如果这个栈顶节点的右子节点为空或者已经输出过了,那么就将这个栈顶节点从栈中跳出,并输出它的值
否则,就将这个栈顶节点的右子树压入栈中,重复循环操作
*/
popStack(s,k);
pre = k;
printf("%5d",k.val);
}else{
t = k.right;
}
}
}
/*
利用迭代循环实现树的中序遍历
基本思路:利用堆栈实现的
基本步骤:
1、判断当前的节点或者栈是否为空,如果其中至少有一个不为空,那么
这时候将进入循环
2、判断当前的节点是否为空,(必须要判断,因为进入外部循环的循环条件有两个,所以不知道是否因为当前
节点是否为空),如果节点不为空,那么将当前的节点压入栈中,然后当前的节点变成它的左节点,将它的左子树压入
栈中
3、判断栈是否为空,将栈顶节点跳出,并将其输出,然后后去这个跳出节点的右子节点
*/
void InOrderTraversal(Node *root){
Stack *s;
Node *t = root,k;
if(!createStack(s)){
printf("创建栈失败!!!\n");
return;
}
while(t != NULL || !isEmpty(s)){
while(t != NULL){
pushStack(s,t);//将当前的节点及其左子树压入栈中
t = t->left;
}
if(!isEmpty(s)){
//从栈中跳出最后一个左子节点的父节点
popStack(s,k);
printf("%5d",k.val);
t = k.right;//将其右子数压入栈中
}
}
}
/*
前序遍历的非递归实现:
基本思路:利用栈实现的
1、如果当前节点不为空或者当前栈不为空,那么就进入循环语句
2、如果当前的节点不为空,那么这时候将当前的节点输出,然后将当前节点压入栈中
然后这个节点往它的左子节点的方向移动,重复2的步骤,知道左子节点为空
3、如果栈不为空,那么就从栈中跳出一个节点,然后将往这个节点的右子树方向移动
4、重复上面的2、3步骤
*/
void preOrderTraversal(Node *root){
Stack *s;
if(!createStack(s)){
printf("创建栈失败!!!\n");
return;
}
Node *t = root,k;
while(t != NULL || !isEmpty(s)){
//当前的节点不为空,或者栈不为空,那么就继续进循环
while(t!= NULL){
//如果当前的节点不为空,那么就将当前的节点输出,然后将它的左子树压入栈中
printf("%5d",t->val);//由于是前序遍历,那么先输出父节点的值
pushStack(s,t);
t = t->left;
}
if(!isEmpty(s)){
//如果栈不为空,那么这时候,将从栈中跳出一个节点,并且将获得它的右子树,然后将右子树压入栈中
popStack(s,k);
t = k.right;//将右子树重复上面的操作
}
}
}
int main(){
int n,i,val;
Node *root = NULL;
printf("请输入树的节点个数:");
scanf("%d",&n);
printf("请输入各个节点的值:");
for(i = 0; i < n; i++){
scanf("%d",&val);
root = insert(root,val);
}
printf("递归实现树的中序遍历:");
InOrderDisplay(root);
printf("\n");
printf("迭代实现数的中序遍历:");
InOrderTraversal(root);
printf("\n");
printf("递归实现树的前序遍历:");
preOrderDisplay(root);
printf("\n");
printf("迭代实现树的前序遍历:");
preOrderTraversal(root);
printf("\n");
printf("递归实现树的后序遍历:");
postOrderDisplay(root);
printf("\n");
printf("迭代实现树的后序遍历:");
postOrderTraversal(root);
printf("\n");
return 0;
}
运行结果:

层序遍历
二叉搜索树的层序遍历,需要使用到队列。
基本思路:
1·、定义一个队列
2、创建二叉搜索树
3、将当前的根节点压入到队列中
4、当队列不为空的时候,那么我们将从队列中跳出节点,将它的值输出,然后判断它的左右子节点是否为空,如果不为空,那么我们就将他们压入到队列中
5、重复4的操作,直到队列为空,此时层序遍历完成。
代码实现:
/*
实现二叉树的层序遍历基本思路:
利用队列来实现的
1、判断当前的节点是否为空或者队列是否为空,如果
不为空,那么就将当前的节点压入队列,同时需要判断当前
节点的子节点是否为空,如果不为空,那么同样的将它的子节点压入队列中
2、如果把这个节点的子节点压入道队列之后,那么这时候我们需要将从
队列中跳出一个节点,然后将这个节点的信息输出。
3、获取队列头,如果队列头不为空,那么这时候重复2的操作
*/
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 100
#define ERROR 0
#define OK 1
typedef struct NODE * Node;
typedef Node * List;
struct NODE{
int val;
Node left;
Node right;
};
typedef struct QUEUE{
List arr;
int front;//队头指针
int rear;//队尾指针
}Queue;
int init(Queue &s){
s.arr = (List)malloc(sizeof(List) * MAX_SIZE);//定义一个指针类型的数组
if(s.arr == NULL){
return ERROR;
}
int i;
//给数组初始化之后还没有可以,还需要给所有的节点分配空间,如果没有这一步,那么就会发生报错
for(i = 0; i < MAX_SIZE; i++){
s.arr[i] = (Node)malloc(sizeof(struct NODE));
if(s.arr[i] == NULL)
return ERROR;
}
s.front = s.rear = 0;//将队头指针、队尾指针都初始为0
return OK;
}
//压入队列
int pushQueue(Queue &s,Node &node){
if((s.rear + 1) % MAX_SIZE == s.front){
//如果栈满了,返回ERROR
printf("队列为满!!!\n");
return ERROR;
}
s.arr[s.rear] = node;
s.rear = (s.rear + 1) % MAX_SIZE;
return OK;
}
int popQueue(Queue &s,Node &k){
if(s.rear == s.front){
//printf("队列为空!!!\n");
return ERROR;
}
k = s.arr[s.front];
s.front = (s.front + 1) % MAX_SIZE;
return OK;
}
int getTop(Queue &s,Node &k){
if(s.rear == s.front){
//printf("队列为空!!!\n");
return ERROR;
}
k = s.arr[s.front];
return OK;
}
int isEmpty(Queue &s){
return s.rear == s.front;//判断队列是否为空
}
int getSize(Queue &s){
return (s.rear - s.front + MAX_SIZE)%MAX_SIZE;//获取队列的个数
}
/*
利用递归创建二叉查找树
基本思路:
1、首先判断当前的节点是否为空,如果为空,就说明这个位置是新节点要插入的位
置此时需要给新节点分配空间,判断创建节点是否成功,如果失败,那么输出错误信
息,否则将这个节点返回
2、如果当前的节点不为空,那么这时候拿当前节点和新节点的值进行比较,如果
新节点的值大于等于当前的节点,那么意味着新节点会插入在当前节点的右子树位
置,否则插入在当前节点的左子树位置
*/
Node createBinaryTree(Node root,int x){
if(root == NULL){
Node node = (Node)malloc(sizeof(struct NODE));
if(node == NULL){
//printf("创建新节点失败!!!\n");
exit(0);
}
node->val = x;
node->left = NULL;
node->right = NULL;
root = node;
}else{
//如果当前的节点不为空,说明不是要插入的位置,需要和当前节点的值进行
//比较,如果大于等于当前节点的值,那么往右子树的方向进行递归,否则往左子树方向递归
if(x < root->val){
root->left = createBinaryTree(root->left,x);
}else{
root->right = createBinaryTree(root->right,x);
}
}
return root;
}
/*
利用递归实现树的后序遍历
*/
void postOrderTraversal(Node root){
if(root != NULL){
//如果当前的节点不为空,那么就先访问左子树,然后访问右子树,最后访问自身
postOrderTraversal(root->left);
postOrderTraversal(root->right);
printf("%5d",root->val);
}
}
/*
利用递归实现树的前序遍历
*/
void preOrderTraversal(Node root){
if(root != NULL){
printf("%5d",root->val);
preOrderTraversal(root->left);
preOrderTraversal(root->right);
}
}
/*
利用队列实现树的层序遍历
*/
void levelOrderTraversal(Node root){
Node t = root,k;
Queue q;
init(q);
pushQueue(q,t);//将根节点压入队列中
while(!isEmpty(q)){
//如果队列不为空,那么就继续进行循环
popQueue(q,t);//将从队列中跳出一个节点,然后将这个节点的信息输出
printf("%5d",t->val);
/*
判断从队列中跳出的节点是否含有左右子节点,如果含有,那么就将这个节
点的左右子节点压入到队列中
*/
if(t->left != NULL){
pushQueue(q,t->left);
}
if(t->right != NULL){
pushQueue(q,t->right);
}
}
}
/*
为了使层序遍历看的更加直观,我们将定义一个临时变量size,表示在压入队列之前
队列的元素个数,然后将队列中的元素不断跳出,并且输出对应的信息,与此同时,
每跳出一个节点,我们都需要判断这个节点是否含有左右子节点,如果含有,那么就
将它的子节点压入到队列中去
*/
void levelOrderTraversal2(Node root){
Node t = root,k;
Queue q;
int size,i;
init(q);
pushQueue(q,t);//将根节点压入队列中
while(!isEmpty(q)){
size = getSize(q);
for(i = 1; i <= size; i++){
popQueue(q,k);
printf("%5d",k->val);
//每跳出一个节点,那么就将它的左右子节点压入到队列中
if(k->left != NULL){
pushQueue(q,k->left);
}
if(k->right != NULL){
pushQueue(q,k->right);
}
}
printf("\n");
}
}
int main(){
int n,i,val;
printf("请输入节点个数:");
scanf("%d",&n);
printf("请输入各个节点的值:");
Node root = NULL;
//创建二叉查找树
for(i = 0; i < n; i++){
scanf("%d",&val);
root = createBinaryTree(root,val);
}
//实现它的后序遍历
printf("递归实现树的后序遍历:");
postOrderTraversal(root);
printf("\n递归实现树的前序遍历:");
preOrderTraversal(root);
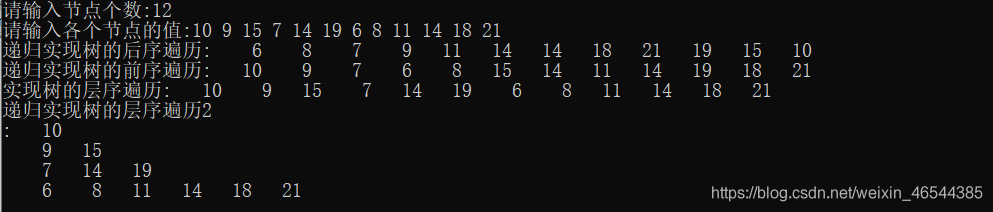
printf("\n实现树的层序遍历:");
levelOrderTraversal(root);
printf("\n递归实现树的层序遍历2\n:");
levelOrderTraversal2(root);
return 0;
}
运行结果:
4、二叉树的高度
求解二叉树某一个节点的高度的时候,我们需要获得这个节点的左右子树的高度,然后将两者中的最大值加1就是当前这个节点的高度.
对应的代码:
//节点
typedef struct NODE{
int val;
struct NODE *left;
struct NODE *right;
}Node;
int getHeight(Node * root){
int hl = 0,hr = 0,max;//hl表示的使左子树的高度,hr表示的使右子树的高度
if(root != NULL){
//当前的节点不为空,获取左右子树的高度
hl = getHeight(root->left);
hr = getHeight(root->right);
max = hl > hr ? hl : hr;
return max + 1;//左右子数高度的最大值加1就是当前节点的高度
}else return 0;//如果当前节点为空,那么它的高度为0
}
5、二叉树的删除
二叉搜索树的删除需要考虑三种情况:删除的节点是一个叶子节点、是一个含有一个子节点的节点、是一个含有两个子节点的节点。需要综合这三种情况进行书写代码。
Node deleteElement(Node root,int x){
if(root == NULL){
printf("节点为空,无法进行删除操作!!!");
}else if(x < root->val){
root->left = deleteElement(root->left,x);
}else if(x > root->val){
root->right = deleteElement(root->right,x);
}else{
/*如果当前的节点是要删除的节点
判断这个删除的节点是否为一个叶节点,如果是,那么直接将其变成NULL即可
否则,如果这个删除节点只有一个子节点,那么就将子节点的值赋值给这个删
除节点,然后将它的子节点变成为NULL,否则,如果这个删除节点含有两个子节点,那么
就将遍历它的右子树,获取右子树中的最小值,然后将这个右子树的最小值赋值给这个
删除节点的值,在将这个最小值变成NULL
*/
if(root->left != NULL && root->right != NULL){
//删除节点含有两个子节点
Node tmp = findMin(root->right);
root->val = tmp->val;
root->right = deleteElement(root->right,tmp->val);
}else{
/*
下面的代码如果使这样写的话,会发生错误的,为什么会这样呢?
其实很简单,因为这里已经包括了两种情况了,删除的节点是一个叶
节点或者只有一个子节点的节点,如果是这样写的话,并没有解决删
除节点是一个叶节点的情况,只是把这个删除节点的内存空间释放了
Node *t = root;
if(root->left != NULL){
root = root->left;
}else if(root->right != NULL){
root = root->right;
}
free(t);//释放删除的节点
*/
Node t = root;
if(root->left == NULL){
/*
如果当前节点的左子节点为空,那么就用它的右子节点替换当前节
点,否则用左子节替换,这样进行判断的好处就是,如果这个删除节点
是一个叶节点,那么两个子节点都是空的,那么这时候root = root-
>right = NULL了,如果这个删除节点含有一个子节点,并且它的左
子节点为空,那么这个节点就用它的右子节点替换,下面的if判断同
理
*/
root = root->right;
}else if(root->right == NULL){
root = root->left;
}
free(t);//释放删除的节点
}
}
return root;
}
6、由几种遍历序列还原二叉树
前序序列、中序序列还原二叉树:
Node getBinaryTree(int preOrder_arr[],int left,int right,int inOrder_arr[],int low,int high){
//结束递归的条件
if(left >= right){
//如果只有一个节点,那么就结束递归
return NULL;
}
int index,root,lcount = 0,rcount = 0;
root = preOrder_arr[left];//有前序序列得到根节点
index = getRoot(inOrder_arr,low,high,root);//在中序数组中获取根节点的下标
//由根节点的下标,我们可以直到左子树有多少个节点,右子树有多少个节点
lcount = index - low;
rcount = high - index - 1;
//创建根节点
Node node = (Node)malloc(sizeof(struct NODE));
node->val = root;
//递归获得根节点的左子树
node->left = getBinaryTree(preOrder_arr,left + 1,left + lcount + 1,inOrder_arr,low,index);
//递归获得根节点的右子树
node->right = getBinaryTree(preOrder_arr,left+lcount + 1,right,inOrder_arr,index + 1,high);
return node;
}
中序序列、后序序列还原二叉树:
//由中序序列、后序序列还原二叉树
Node getBinaryTree2(int inOrder_arr[],int low,int high,int postOrder_arr[],int left,int right){
if(left >= right){
//如果只有一个节点,那么就结束递归
return NULL;
}
int index,root,lcount = 0,rcount = 0;
root = postOrder_arr[right - 1];//后序序列最后一个节点是根节点
index = getRoot(inOrder_arr,low,high,root);//在中序序列中找到根节点的下标
//创建根节点
Node node = (Node)malloc(sizeof(struct NODE));
node->val = root;
//获取左右子数的节点个数
lcount = index - low;
rcount = high - index - 1;
// printf("根节点的左子树有%d个,右子树有%d个\n",lcount,rcount);
//创建按根节点的左子树
node->left = getBinaryTree2(inOrder_arr,low,index,postOrder_arr,left,left + lcount);
//创建根节点的右子树
node->right = getBinaryTree2(inOrder_arr,index + 1,high,postOrder_arr,left + lcount,right - 1);
return node;
}
测试运行代码:
/*
给出两种遍历序列(前序和中序、中序和后序),然后以这两种序列为依据还原二叉树
1、根据前序序列、中序序列还原二叉树
基本思路:
1、定义两个数组,表示两种序列的输出
2、由于前序序列,那么第一个数必定是一个根节点,所以我们有前序
序列,在中序序列中找到根节点对应的下标,从而我们由中序序列也知道了
根节点的左边是他的左子树,右边是他的右子树,那么我们将中序序列就划分成为了
两个子数组,同时也有左、右子数的节点个数,将前序序列也划分成为2哥子数组
3、重复步骤2,直到子数组中的只有一个节点或者没有,这时候结束递归
2、根据中序序列、后序序列还原二叉树
基本思路:和1的一样,只是在由后序序列找到根节点的值有所不同,因为后序序列的根节点
在最后一个,其他的步骤相似
请输入节点的个数:12
请输入前序序列:10 9 7 6 8 15 14 11 14 19 18 21
请输入中序序列:6 7 8 9 10 11 14 14 15 18 19 21
请输入后序序列:6 8 7 9 11 14 14 18 21 19 15 10
*/
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 100
#define ERROR 0
#define OK 1
typedef struct NODE * Node;
typedef Node * List;
struct NODE{
int val;
Node left;
Node right;
};
typedef struct QUEUE{
List arr;
int front;//队头指针
int rear;//队尾指针
}Queue;
int init(Queue &s){
s.arr = (List)malloc(sizeof(List) * MAX_SIZE);//定义一个指针类型的数组
if(s.arr == NULL){
return ERROR;
}
int i;
//给叔组初始化之后还没有可以,还需要给所有的节点分配空间,如果没有这一步,那么就会发生报错
for(i = 0; i < MAX_SIZE; i++){
s.arr[i] = (Node)malloc(sizeof(struct NODE));
if(s.arr[i] == NULL)
return ERROR;
}
s.front = s.rear = 0;//将队头指针、队尾指针都初始为0
return OK;
}
//压入队列
int pushQueue(Queue &s,Node &node){
if((s.rear + 1) % MAX_SIZE == s.front){
//如果栈满了,返回ERROR
printf("队列为满!!!\n");
return ERROR;
}
s.arr[s.rear] = node;
s.rear = (s.rear + 1) % MAX_SIZE;
return OK;
}
int popQueue(Queue &s,Node &k){
if(s.rear == s.front){
//printf("队列为空!!!\n");
return ERROR;
}
k = s.arr[s.front];
s.front = (s.front + 1) % MAX_SIZE;
return OK;
}
int getTop(Queue &s,Node &k){
if(s.rear == s.front){
//printf("队列为空!!!\n");
return ERROR;
}
k = s.arr[s.front];
return OK;
}
int isEmpty(Queue &s){
return s.rear == s.front;//判断队列是否为空
}
int getSize(Queue &s){
return (s.rear - s.front + MAX_SIZE)%MAX_SIZE;//获取队列的个数
}
//利用递归构建二叉树
Node createBinaryTree(Node root,int x){
if(root == NULL){
root = (Node )malloc(sizeof(struct NODE));
if(root == NULL){
printf("创建节点失败!!!\n");
exit(0);
}
root->val = x;
root->left = NULL;
root->right = NULL;
}else{
//如果根节点不为空,那么就绪要找打新节点的位置
if(x < root->val){
//如果新节点的值比当前节点的值小,那么就需要将其往当前节点的左子树方向找
root->left = createBinaryTree(root->left,x);
}else{
root->right = createBinaryTree(root->right,x);
}
}
return root;
}
//层序遍历
void levelOrderTraversal2(Node root){
Node t = root,k;
Queue q;
int size,i,count = 1;
init(q);
pushQueue(q,t);//将根节点压入队列中
while(!isEmpty(q)){
size = getSize(q);
for(i = 1; i <= size; i++){
popQueue(q,k);
printf("%5d",k->val);
//每跳出一个节点,那么就将它的左右子节点压入到队列中
if(k->left != NULL){
pushQueue(q,k->left);
}
if(k->right != NULL){
pushQueue(q,k->right);
}
}
printf("\n");
}
}
//通过循环找树中的最小值
Node findMin(Node root){
Node current = root;
while(current->left != NULL){
current = current->left;
}
return current;
}
//获取二叉搜索树的高度
int getHeight(Node root){
int hl = 0,hr = 0,max;//hl表示的使左子树的高度,hr表示的使右子树的高度
if(root != NULL){
//当前的节点不为空,获取左右子树的高度
hl = getHeight(root->left);
hr = getHeight(root->right);
max = hl > hr ? hl : hr;
return max + 1;//左右子数高度的最大值加1就是当前节点的高度
}else return 0;//如果当前节点为空,那么它的高度为0
}
/*
查找值为x的节点,然后将其返回
*/
Node findElement(Node root,int x){
Node current = root;
while(current != NULL){
if(x < current->val)//如果当前的节点的值大于x的值,那么就往左子树的方向进行查找
current = current->left;
else if(x > current->val)
current = current->right;
else
return current;
}
return NULL;//如果退出循环了,说明没有办法找到x的节点
}
/*
删除值为x的节点(如果x出现了多次,那么就会删除第一个x)
这时候我们需要将分为几种情况进行讨论:
1、删除的节点是一个叶节点,直接将这个节点释放即可
2、如果删除的节点含有一个子节点,那么这时候我们将这个删除节点的子节点
替换掉这个节点即可
3、如果这个删除节点含有两个子节点,那么我们将它的右子树中的最小节点的值赋给
当前节点的值,那么这时候变成了删除右子树中的最小节点了(即前面的两种情况)
*/
Node deleteElement(Node root,int x){
if(root == NULL){
printf("节点为空,无法进行删除操作!!!");
}else if(x < root->val){
root->left = deleteElement(root->left,x);
}else if(x > root->val){
root->right = deleteElement(root->right,x);
}else{
/*如果当前的节点是要删除的节点
判断这个删除的节点是否为一个叶节点,如果是,那么直接将其变成NULL即可
否则,如果这个删除节点只有一个子节点,那么就将子节点的值赋值给这个删
除节点,然后将它的子节点变成为NULL,否则,如果这个删除节点含有两个子节点,那么
就将遍历它的右子树,获取右子树中的最小值,然后将这个右子树的最小值赋值给这个
删除节点的值,在将这个最小值变成NULL
*/
if(root->left != NULL && root->right != NULL){
//删除节点含有两个子节点
Node tmp = findMin(root->right);
root->val = tmp->val;
root->right = deleteElement(root->right,tmp->val);
}else{
/*
下面的代码如果使这样写的话,会发生错误的,为什么会这样呢?
其实很简单,因为这里已经包括了两种情况了,删除的节点是一个叶
节点或者只有一个子节点的节点,如果是这样写的话,并没有解决删
除节点是一个叶节点的情况,只是把这个删除节点的内存空间释放了
Node *t = root;
if(root->left != NULL){
root = root->left;
}else if(root->right != NULL){
root = root->right;
}
free(t);//释放删除的节点
*/
Node t = root;
if(root->left == NULL){
/*
如果当前节点的左子节点为空,那么就用它的右子节点替换当前节
点,否则用左子节替换,这样进行判断的好处就是,如果这个删除节点
是一个叶节点,那么两个子节点都是空的,那么这时候root = root-
>right = NULL了,如果这个删除节点含有一个子节点,并且它的左
子节点为空,那么这个节点就用它的右子节点替换,下面的if判断同
理
*/
root = root->right;
}else if(root->right == NULL){
root = root->left;
}
free(t);//释放删除的节点
}
}
return root;
}
//利用递归的方式实现后序遍历
void postOrderDisplay(Node root){
if(root != 0){
postOrderDisplay(root->left);
postOrderDisplay(root->right);
printf("%d ",root->val);
}
}
//利用递归的方式实现前序遍历
void preOrderDisplay(Node root){
if(root != 0){
printf("%d ",root->val);
preOrderDisplay(root->left);
preOrderDisplay(root->right);
}
}
void input(int arr[],int n){
int i;
for(i = 0; i < n; i++)
scanf("%d",&arr[i]);
}
int getRoot(int inOrder_arr[],int low,int high,int x){
int i;
for(i = low; i < high; i++){
if(inOrder_arr[i] == x)
return i;
}
return -1;
}
Node getBinaryTree(int preOrder_arr[],int left,int right,int inOrder_arr[],int low,int high){
//结束递归的条件
if(left >= right){
//如果只有一个节点,那么就结束递归
return NULL;
}
int index,root,lcount = 0,rcount = 0;
root = preOrder_arr[left];//有前序序列得到根节点
index = getRoot(inOrder_arr,low,high,root);//在中序数组中获取根节点的下标
//由根节点的下标,我们可以直到左子树有多少个节点,右子树有多少个节点
lcount = index - low;
rcount = high - index - 1;
//创建根节点
Node node = (Node)malloc(sizeof(struct NODE));
node->val = root;
//递归获得根节点的左子树
node->left = getBinaryTree(preOrder_arr,left + 1,left + lcount + 1,inOrder_arr,low,index);
//递归获得根节点的右子树
node->right = getBinaryTree(preOrder_arr,left+lcount + 1,right,inOrder_arr,index + 1,high);
return node;
}
//由中序序列、后序序列还原二叉树
Node getBinaryTree2(int inOrder_arr[],int low,int high,int postOrder_arr[],int left,int right){
if(left >= right){
//如果只有一个节点,那么就结束递归
return NULL;
}
int index,root,lcount = 0,rcount = 0;
root = postOrder_arr[right - 1];//后序序列最后一个节点是根节点
index = getRoot(inOrder_arr,low,high,root);//在中序序列中找到根节点的下标
//创建根节点
Node node = (Node)malloc(sizeof(struct NODE));
node->val = root;
//获取左右子数的节点个数
lcount = index - low;
rcount = high - index - 1;
// printf("根节点的左子树有%d个,右子树有%d个\n",lcount,rcount);
//创建按根节点的左子树
node->left = getBinaryTree2(inOrder_arr,low,index,postOrder_arr,left,left + lcount);
//创建根节点的右子树
node->right = getBinaryTree2(inOrder_arr,index + 1,high,postOrder_arr,left + lcount,right - 1);
return node;
}
int main(){
int preOrder_arr[MAX_SIZE],inOrder_arr[MAX_SIZE],postOrder_arr[MAX_SIZE];//定义两个数组,分别表示前序序列、中序序列
int n,i;
Node root;
printf("请输入节点的个数:");
scanf("%d",&n);
printf("请输入前序序列:");
input(preOrder_arr,n);
printf("请输入中序序列:");
input(inOrder_arr,n);
printf("请输入后序序列:");
input(postOrder_arr,n);
root = getBinaryTree(preOrder_arr,0,n,inOrder_arr,0,n);
printf("递归实现由前序序列、中序序列还原的二叉树的后序遍历:");
postOrderDisplay(root);
printf("\n");
root = getBinaryTree2(inOrder_arr,0,n,postOrder_arr,0,n);
printf("递归实现由中序序列、后序序列还原的二叉树的前序遍历:");
preOrderDisplay(root);
printf("\n两种序列还原的二叉树的高度为:");
printf("%d\n",getHeight(root));
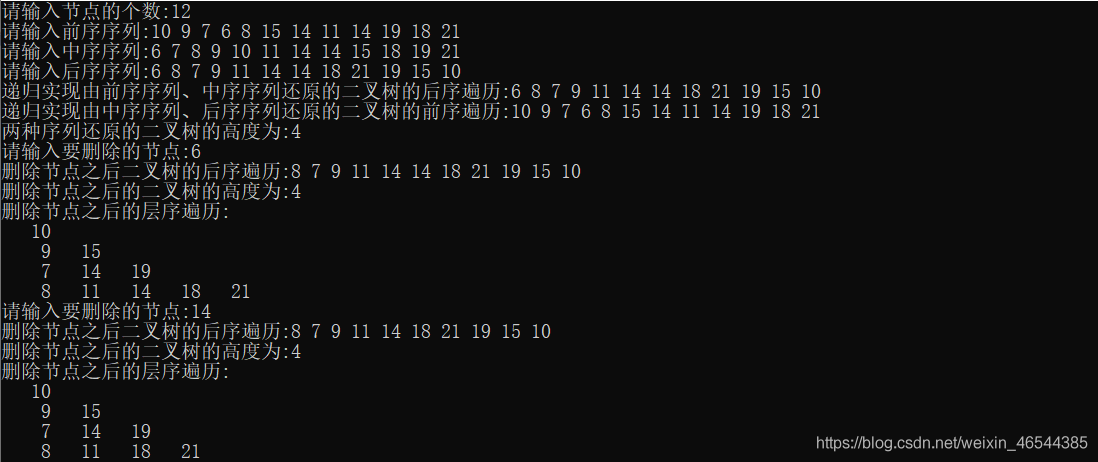
printf("请输入要删除的节点:");
while(scanf("%d",&n) != EOF){
if(n == 0)
break;
root = deleteElement(root,n);
printf("删除节点之后二叉树的后序遍历:");
postOrderDisplay(root);
printf("\n删除节点之后的二叉树的高度为:");
printf("%d\n",getHeight(root));
printf("删除节点之后的层序遍历:\n");
levelOrderTraversal2(root);
printf("请输入要删除的节点:");
}
return 0;
}
运行结果:
所有应用的完整代码:
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 100
#define INCREMENT 10
#define ERROR 0
#define OK 1
typedef struct NODE * Node;
typedef Node * List;//定义二重指针
struct NODE{
int val;
Node left,right;
};
typedef struct QUEUE{
List arr;
int front;//队头指针
int rear;//队尾指针
}Queue;
int init(Queue &s){
s.arr = (List)malloc(sizeof(List) * MAX_SIZE);//定义一个指针类型的数组
if(s.arr == NULL){
return ERROR;
}
int i;
//给叔组初始化之后还没有可以,还需要给所有的节点分配空间,如果没有这一步,那么就会发生报错
for(i = 0; i < MAX_SIZE; i++){
s.arr[i] = (Node)malloc(sizeof(struct NODE));
if(s.arr[i] == NULL)
return ERROR;
}
s.front = s.rear = 0;//将队头指针、队尾指针都初始为0
return OK;
}
//压入队列
int pushQueue(Queue &s,Node &node){
if((s.rear + 1) % MAX_SIZE == s.front){
//如果栈满了,返回ERROR
printf("队列为满!!!\n");
return ERROR;
}
s.arr[s.rear] = node;
s.rear = (s.rear + 1) % MAX_SIZE;
return OK;
}
int popQueue(Queue &s,Node &k){
if(s.rear == s.front){
//printf("队列为空!!!\n");
return ERROR;
}
k = s.arr[s.front];
s.front = (s.front + 1) % MAX_SIZE;
return OK;
}
int getTop(Queue &s,Node &k){
if(s.rear == s.front){
//printf("队列为空!!!\n");
return ERROR;
}
k = s.arr[s.front];
return OK;
}
int isEmpty(Queue &s){
return s.rear == s.front;//判断队列是否为空
}
int getSize(Queue &s){
return (s.rear - s.front + MAX_SIZE)%MAX_SIZE;//获取队列的个数
}
typedef struct STACK{
List arr;
int top;
}Stack;
//初始化栈
int init(Stack &stack){
stack.arr = (List)malloc(sizeof(List) * MAX_SIZE);//创建一个指针数组
if(stack.arr == NULL){
printf("创建节点数组失败!!!\n");
return ERROR;
}
//在创建完指针数组之后,还需要将它的节点进行分配空间,否则会发生错误
int i;
for(i = 0; i < MAX_SIZE; i++){
stack.arr[i] = (Node)malloc(sizeof(struct NODE));
if(stack.arr[i] == NULL){
printf("创建节点失败!!!\n");
return ERROR;
}
}
stack.top = 0;
return OK;
}
//压栈
int push(Stack &stack,Node node){
if(stack.top >= MAX_SIZE){
//如果栈满了,那么我们需要重新分配空间
List newBase = (List)realloc(stack.arr,sizeof(List) * (MAX_SIZE + INCREMENT));
if(newBase == NULL){
printf("重新分配空间失败!!!\n");
return ERROR;
}
stack.arr = newBase;
}
stack.arr[stack.top++] = node;
return OK;
}
//出栈
int pop(Stack &stack,Node &k){
if(stack.top == 0)
return ERROR;
k = stack.arr[--stack.top];
return OK;
}
int isEmpty(Stack &stack){
return stack.top == 0;
}
//利用递归创建二叉树
Node createTree(Node T,int x){
if(T == NULL){
T = (Node)malloc(sizeof(struct NODE));
if(T == NULL){
//如果分配空间错误,那么输出对应的信息,然后退出虚拟机
printf("创建节点错误");
exit(0);
}
T->val = x;
T->left = NULL;
T->right = NULL;
}else{
//如果当前的节点不为空,那么就需要找到x的位置
if(x < T->val)
T->left = createTree(T->left,x);
else
T->right = createTree(T->right,x);
}
/*
int isLeftChild = 0;
Node *current = T,*parent = NULL,*node = (Node *)malloc(sizeof(Node));
while(current != NULL){
parent = current;
if(x < current->val){
current = current->left;
isLeftChild = 1;
}else{
current = current->right;
isLeftChild = 0;
}
}
node->val = x;
node->left = NULL;
node->right = NULL;
if(parent == NULL){
T = node;
}else{
if(isLeftChild){
parent->left = node;
}else{
parent->right = node;
}
}
*/
return T;
}
//利用非递归的方式进行前序遍历(这时候需要用到栈)
void preOrderDisplay(Node t){
Stack stack;
init(stack);
Node root = t,tmp;
while(root != NULL || !isEmpty(stack)){
while(root !=NULL){
//将左子数的所有节点压入到栈中
/*
if(root->left == NULL && root->right == NULL)
printf("%d ",root->val);//将叶子节点输出
*/
printf("%d ",root->val);
push(stack,root);
root = root->left;
}
if(!isEmpty(stack)){
//如果栈不为空,那么我们需要从栈中跳出一个节点
pop(stack,root);
root = root->right;
}
}
}
//层序遍历
void levelOrderTraversal2(Node root){
Node t = root,k;
Queue q;
int size,i,count = 1;
init(q);
pushQueue(q,t);//将根节点压入队列中
while(!isEmpty(q)){
size = getSize(q);
for(i = 1; i <= size; i++){
popQueue(q,k);
printf("%5d",k->val);
//每跳出一个节点,那么就将它的左右子节点压入到队列中
if(k->left != NULL){
pushQueue(q,k->left);
}
if(k->right != NULL){
pushQueue(q,k->right);
}
}
printf("\n");
}
}
void preOrderDisplay2(Node root){
if(root != NULL){
/* if(root->left == NULL && root->right == NULL)
printf("%d ",root->val);//通过前序遍历,将所有的叶子节点输出
*/
printf("%5d",root->val);
preOrderDisplay2(root->left);
preOrderDisplay2(root->right);
}
}
Node findMin(Node root){
Node current = root;
while(current->left != NULL){
current = current->left;
}
return current;
}
Node deleteElement(Node root,int x){
if(root == NULL){
printf("节点为空,无法进行删除操作!!!");
}else if(x < root->val){
root->left = deleteElement(root->left,x);
}else if(x > root->val){
root->right = deleteElement(root->right,x);
}else{
/*如果当前的节点是要删除的节点
判断这个删除的节点是否为一个叶节点,如果是,那么直接将其变成NULL即可
否则,如果这个删除节点只有一个子节点,那么就将子节点的值赋值给这个删
除节点,然后将它的子节点变成为NULL,否则,如果这个删除节点含有两个子节点,那么
就将遍历它的右子树,获取右子树中的最小值,然后将这个右子树的最小值赋值给这个
删除节点的值,在将这个最小值变成NULL
*/
if(root->left != NULL && root->right != NULL){
//删除节点含有两个子节点
Node tmp = findMin(root->right);
root->val = tmp->val;
root->right = deleteElement(root->right,tmp->val);
}else{
/*
下面的代码如果使这样写的话,会发生错误的,为什么会这样呢?
其实很简单,因为这里已经包括了两种情况了,删除的节点是一个叶
节点或者只有一个子节点的节点,如果是这样写的话,并没有解决删
除节点是一个叶节点的情况,只是把这个删除节点的内存空间释放了
Node *t = root;
if(root->left != NULL){
root = root->left;
}else if(root->right != NULL){
root = root->right;
}
free(t);//释放删除的节点
*/
Node t = root;
if(root->left == NULL){
/*
如果当前节点的左子节点为空,那么就用它的右子节点替换当前节
点,否则用左子节替换,这样进行判断的好处就是,如果这个删除节点
是一个叶节点,那么两个子节点都是空的,那么这时候root = root-
>right = NULL了,如果这个删除节点含有一个子节点,并且它的左
子节点为空,那么这个节点就用它的右子节点替换,下面的if判断同
理
*/
root = root->right;
}else if(root->right == NULL){
root = root->left;
}
free(t);//释放删除的节点
}
}
return root;
}
/*
获取二叉树的高度:等于左右子树高度的最大值加上1,那么
我们需要可以通过递归来获取当前节点的左右子树的高度,然后
将左右子树的高度加1就是当前这个节点的高度了
*/
int getHeight(Node t){
int hl = 0,hr = 0,max;//hl表示当前节点的左子树的高度,hr表示的是当前节点的右子树的高度
if(t != NULL){
//注意这里不是+=,而是直接赋值
hl = getHeight(t->left);
hr = getHeight(t->right);
max = hl > hr ? hl : hr;
return (max + 1);
}else return 0;
}
int main(){
Node root = NULL;
int n,i,x;
scanf("%d",&n);
for(i = 0; i < n; i++){
scanf("%d",&x);
root = createTree(root,x);
}
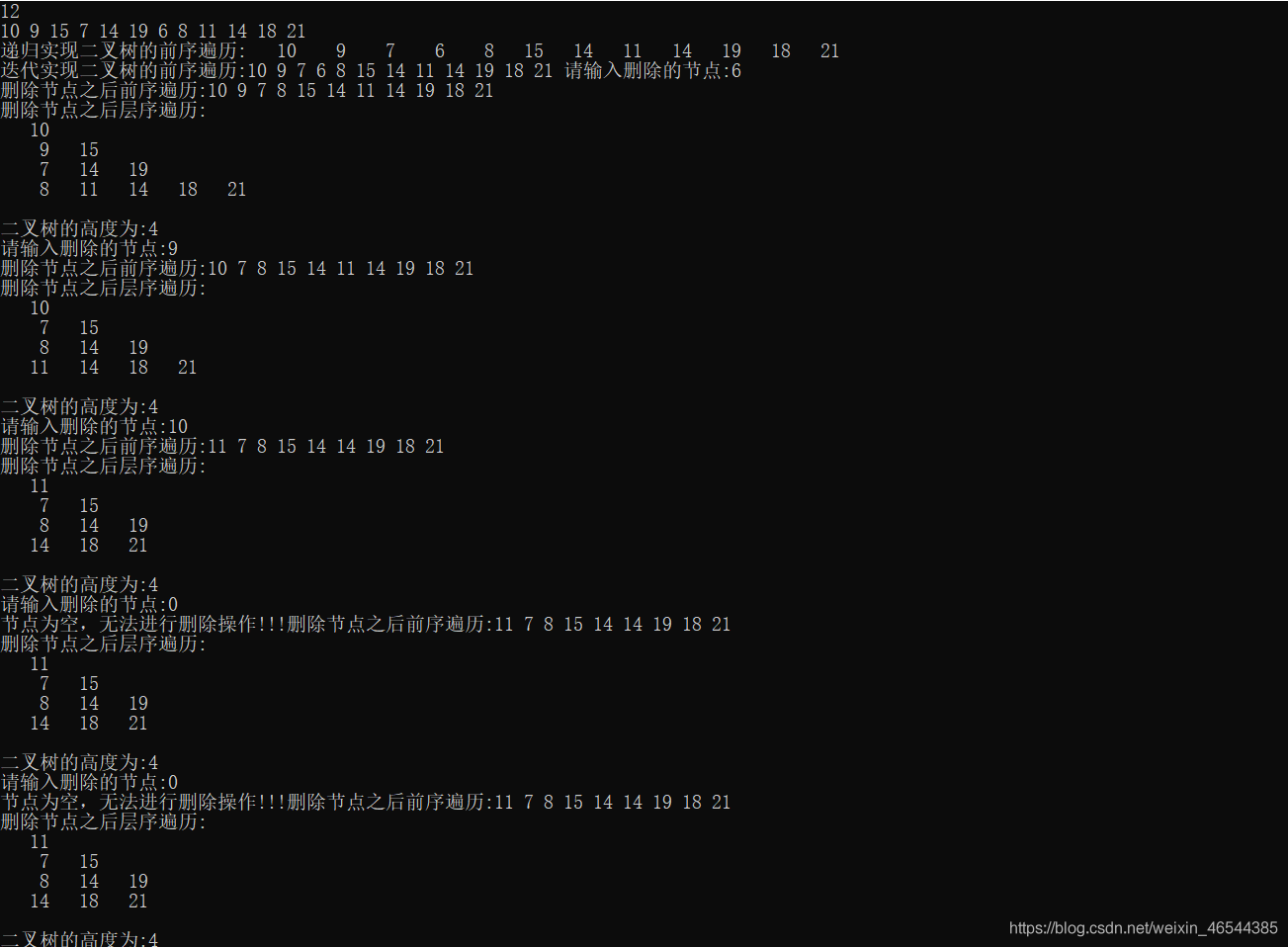
printf("递归实现二叉树的前序遍历:");
preOrderDisplay2(root);
printf("\n迭代实现二叉树的前序遍历:");
preOrderDisplay(root);
printf("请输入删除的节点:");
while(scanf("%d",&n) != EOF){
deleteElement(root,n);
printf("删除节点之后前序遍历:");
preOrderDisplay(root);
printf("\n删除节点之后层序遍历:\n");
levelOrderTraversal2(root);
printf("\n二叉树的高度为:%d\n",getHeight(root));
printf("请输入删除的节点:");
}
return 0;
}
运行结果:
加载全部内容