python信号时域统计特征提取 python实现信号时域统计特征提取代码
focusxy 人气:01.实验数据需求
为了对采集的压力实验数据做特征工程,需要对信号进行时域的统计特征提取,包含了均值、均方根、偏度、峭度、波形因子、波峰因子、脉冲因子、峭度因子等,现用python对其进行实现。
2.python实现
其中的输入参数含义:
① data:实验数据的DataFrame
② p1:所截取实验信号的起始采样点位置
③ p2:所截取实验信号的终止采样点位置
from pandas import Series import math pstf_list=[] def psfeatureTime(data,p1,p2): #均值 df_mean=data[p1:p2].mean() #方差 df_var=data[p1:p2].var() #标准差 df_std=data[p1:p2].std() #均方根 df_rms=math.sqrt(pow(df_mean,2) + pow(df_std,2)) #偏度 df_skew=data[p1:p2].skew() #峭度 df_kurt=data[p1:p2].kurt() sum=0 for i in range(p1,p2): sum+=math.sqrt(abs(data[i])) #波形因子 df_boxing=df_rms / (abs(data[p1:p2]).mean()) #峰值因子 df_fengzhi=(max(data[p1:p2])) / df_rms #脉冲因子 df_maichong=(max(data[p1:p2])) / (abs(data[p1:p2]).mean()) #裕度因子 df_yudu=(max(data[p1:p2])) / pow((sum/(p2-p1)),2) featuretime_list = [df_mean,df_rms,df_skew,df_kurt,df_boxing,df_fengzhi,df_maichong,df_yudu] return featuretime_list
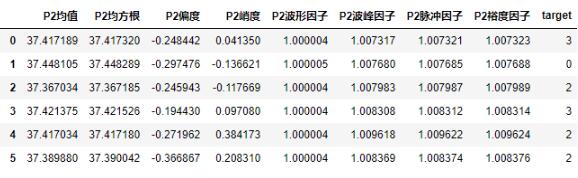
3.结果与说明
补充拓展:python数据结构与算法--回溯算法详解
回溯算法:一种优先搜索算法(试探法);按优条件向前搜索,以达目标;当试探到某步,发现原来选择并不好(走不通),就退回重新选择。
回溯算法的一般步骤:1:定义问题的解空间(搜索中动态生成);2:确定易搜索的解空间结构(一般为树形结构或图);3:以深度优先的方式搜索解空间,搜索中用剪枝函数避免无效搜索。
剪枝函数:1:用约束函数在扩展节点处减去不满足约束条件的子树;2:用限界函数减去不能得到最优解的子树。
回溯法:实战
1:电话号码的字母组合
方法:回溯(适用于组合问题)
class Solution:
def letterCombination(self,digits):
phone={'2': ['a', 'b', 'c'],
'3': ['d', 'e', 'f'],
'4': ['g', 'h', 'i'],
'5': ['j', 'k', 'l'],
'6': ['m', 'n', 'o'],
'7': ['p', 'q', 'r', 's'],
'8': ['t', 'u', 'v'],
'9': ['w', 'x', 'y', 'z']}
res=[]#存放组合结果
def backtrack(combination,next_digits):#回溯函数
#combination目前已经产生的组合,next_digits:输入的下一个字符
if len(next_digits)==0: #递归出口
res.append(combination)
else:
for i in phone[next_digits[0]]:
backtrack(combination+i,next_digits[1:]) #递归实现回溯
if digits:
backtrack('',digits) #初始化
return res
2:全排列
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
class Solution:
def permute(self,nums):
res=[] #存放组合结果
size=len(nums)
def backtrack(combination,nums):
#combination目前已经产生的组合,nums为剩下的数组
#递归出口
#递归的结束一定 要有return
if len(combination)==size:
res.append(combination)
return #注意
for i in range(len(nums)):
backtrack(combination+[nums[i]],nums[:i]+nums[i+1:]) #递归回溯
backtrack([],nums)
return res
if __name__=='__main__':
nums = [1,2,3]
solution=Solution()
print(solution.permute(nums))
3:数字组合
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
class Solution:
def combinationArray(self,candidates,target):
candidates.sort()
res=[] #存放组合结果
size=len(candidates)
def backtrack(combination,cur_sum,j):
#combination目前已经产生的组合,cur_sum当前计算和,j用于控制求和的查找范围起点
#递归出口
if cur_sum>target:
return
if cur_sum==target:
res.append(combination)
for i in range(j,size): #j避免重复
if cur_sum+candidates[i]>target: #约束函数(剪)
break
j=i
backtrack(combination+[candidates[i]],cur_sum+candidates[i],j)#递归回溯
backtrack([],0,0)
return res
if __name__=='__main__':
candidates = [2,3,6,7]
target = 7
solution=Solution()
print(solution.combinationArray(candidates,target))
4:
N皇后问题
class Solution:
def solveNqueen(self,n):
res=[] #存放结果组合,对于N皇后问题,这里存放的是其放在每一行对应的列下标
def backtrack(combination):
if len(combination)==n:
res.append(combination)
return
for j in range(n):
if combination:
#排除当前行,列和对应的两个对角线。
if j not in combination and j!=combination[-1]+1 and j!=combination[-1]-1:#约束条件
backtrack(combination+[j]) #递归回溯
else:
continue
else:
backtrack(combination+[j])
backtrack([]) #回溯初始化
#转化为需要的格式
output=[["." * k + "Q" + "." * (n - k - 1) for k in i] for i in res] #列表生成器
return output
if __name__=='__main__':
n=4
solution=Solution()
print(solution.solveNqueen(n))
5:子集
[1,2,3]的子集[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res=[]#存放组合结果
size=len(nums)
def backtrack(combination,nums):
#combination目前已经产生的组合,nums为剩下的数组
if len(combination)<=size:
res.append(combination)
#递归出口
#递归的结束一定 要有return
if len(combination)==size:
return
for i in range(len(nums)):
backtrack(combination+[nums[i]],nums[i+1:]) #递归回溯
backtrack([],nums)
return res
if __name__=='__main__':
nums=[1,2,3]
solution=Solution()
print(solution.subsets(nums))
6:
字母大小写的全排列
给定一个字符串S,通过将字符串S中的每个字母转变大小写,我们可以获得一个新的字符串。返回所有可能得到的字符串集合。
输入: S = "a1b2"
输出: ["a1b2", "a1B2", "A1b2", "A1B2"]
class Solution:
def letterpermute(self,S):
res=[]
size=len(S)
def backtrack(combination,S):
if len(combination)==size:
res.append(''.join(combination))
return
for i in range(len(S)):
if "a"<=S[i]<= "z" or "A"<=S[i]<= "Z":
for j in range(2):
if j==0:
backtrack(combination+[S[i].lower()],S[i+1:])
if j==1:
backtrack(combination+[S[i].upper()],S[i+1:])
else:
backtrack(combination+[S[i]],S[i+1:])
backtrack([],S)
return res
if __name__=='__main__':
S=[i for i in "1B2"]
solution=Solution()
print(solution.letterpermute(S))
7:生成括号
括号生成:给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
class Solution:
def generateParenthesis(self,n):
res=[] #存放组合结果
def backtrack(combination,left,right):
#combination目前已经产生的组合
if len(combination)==2*n: #递归出口
res.append(combination)
#对于有效的括号,左边先出
if left<n:
backtrack(combination+'(',left+1,right)#递归实现回溯
if right<left:
backtrack(combination+')',left,right+1)#递归实现回溯
backtrack('',0,0) #初始化
return res
if __name__=='__main__':
n=3
solution=Solution()
print(solution.generateParenthesis(n))
以上这篇python实现信号时域统计特征提取代码就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持。
加载全部内容