Python 图像压缩 在Python中使用K-Means聚类和PCA主成分分析进行图像压缩
deephub 人气:5在Python中使用K-Means聚类和PCA主成分分析进行图像压缩
各位读者好,在这片文章中我们尝试使用sklearn库比较k-means聚类算法和主成分分析(PCA)在图像压缩上的实现和结果。 压缩图像的效果通过占用的减少比例以及和原始图像的差异大小来评估。 图像压缩的目的是在保持与原始图像的相似性的同时,使图像占用的空间尽可能地减小,这由图像的差异百分比表示。 图像压缩需要几个Python库,如下所示:
# image processing from PIL import Image from io import BytesIO import webcolors # data analysis import math import numpy as np import pandas as pd # visualization import matplotlib.pyplot as plt from importlib import reload from mpl_toolkits import mplot3d import seaborn as sns # modeling from sklearn.cluster import KMeans from sklearn.decomposition import PCA from sklearn.preprocessing import MinMaxScaler
探索图像

每个颜色通道的图像
图像中的每个像素都可以表示为三个0到255之间的8位无符号(正)整数,或缩放为三个0到1之间的无符号(正)浮点数。这三个值分别指定红色,绿色,蓝色的强度值,这通常称为RGB编码。 在此文章中,我们使用了220 x 220像素的lena.jpg,这是在图像处理领域广泛使用的标准测试图像。
ori_img = Image.open("images/lena.png")
ori_img

原始图像
X = np.array(ori_img.getdata()) ori_pixels = X.reshape(*ori_img.size, -1) ori_pixels.shape
图像储存方式是形状为(220、220、3)的3D矩阵。 前两个值指定图像的宽度和高度,最后一个值指定RBG编码。 让我们确定图像的其他属性,即图像大小(以千字节(KB)为单位)和原色的数量。
def imageByteSize(img): img_file = BytesIO() image = Image.fromarray(np.uint8(img)) image.save(img_file, 'png') return img_file.tell()/1024 ori_img_size = imageByteSize(ori_img) ori_img_n_colors = len(set(ori_img.getdata()))
lena.jpg的原始图像大小为86 KB,并具有37270种独特的颜色。 因此,我们可以说lena.jpg中的两个像素具有相同的精确RGB值的可能性很小。
接下来,让我们计算图像的差异作为压缩结果的基准。
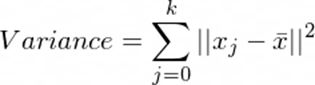
ori_img_total_variance = sum(np.linalg.norm(X - np.mean(X, axis = 0), axis = 1)**2)
我们得到方差为302426700.6427498。 但是我们无法解释方差本身的价值。 我们稍后将在K-Means聚类中使用它。
k-means聚类
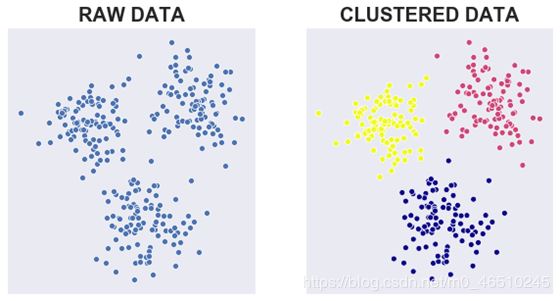
具有三个聚类中心的二维k-means聚类图像
算法
k-means聚类是一种常用的无监督学习算法,用于将数据集划分为k个聚类中心,其中k必须由用户预先指定。 该算法的目标是将现有数据点分类为几个集群,以便:
- 同一集群中的数据尽可能相似
- 来自不同集群的数据尽可能不同
每个集群由聚类中心表示,聚类中心是聚类数据点的平均值。 这是算法:
- 用户指定集群数k
- 从数据集中随机选择k个不同的点作为初始聚类中心
- 将每个数据点分配给最近的聚类中心,通常使用欧几里得距离
- 通过取属于该集群的所有数据点的平均值来计算新聚类中心
- 重复步骤3和4,直到收敛为止,即聚类中心位置不变
请注意,结果可能并不理想,因为它取决于随机的初始化。
理念
我们的原始图像包含数千种颜色。 我们将利用K-Means聚类算法来减少颜色数量,因此它仅需要存储一定数量的RGB值。 我们将减小图像尺寸使其更有效率地进行储存。 我们可以将像素值视为具有(宽度×高度)观察值和3个与RGB值相对应的特征的数据帧。 对于lena.jpg,我们将具有220×220(48400)个观测值和3个特征。
因此,我们可以可视化三维图中的每个像素。 这是前220个像素,代表原始图像中的第一行像素。
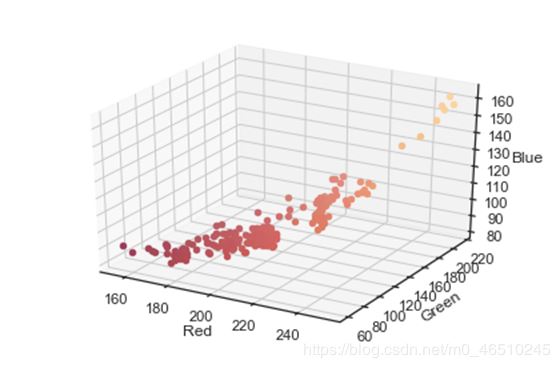
像素值的三维图
简单的例子
在我们对颜色数k使用各种值进行迭代之前,让我们使用k = 2来了解我们的目的。 到本节末,我们希望图像只有2种颜色。 首先,我们创建一个KMeans对象,该对象适合我们的原始像素X。
kmeans = KMeans(n_clusters = 2,
n_jobs = -1,
random_state = 123).fit(X)
kmeans_df = pd.DataFrame(kmeans.cluster_centers_, columns = ['Red', 'Green', 'Blue'])
然后我们将RGB值转换为其英文颜色名称:
def closest_colour(requested_colour):
min_colours = {}
for key, name in webcolors.CSS3_HEX_TO_NAMES.items():
r_c, g_c, b_c = webcolors.hex_to_rgb(key)
rd = (r_c - requested_colour[0]) ** 2
gd = (g_c - requested_colour[1]) ** 2
bd = (b_c - requested_colour[2]) ** 2
min_colours[(rd + gd + bd)] = name
return min_colours[min(min_colours.keys())]
def get_colour_name(requested_colour):
try:
closest_name = actual_name = webcolors.rgb_to_name(requested_colour)
except ValueError:
closest_name = closest_colour(requested_colour)
return closest_name
kmeans_df["Color Name"] = list(map(get_colour_name, np.uint8(kmeans.cluster_centers_)))
kmeans_df
当我们指定2为n_clusters参数值时,我们得到两个聚类中心。下一步,我们可以通过聚类中心来表示该群集中的每个像素值。 因此,在压缩图像中将只有两个像素值。
def replaceWithCentroid(kmeans):
new_pixels = []
for label in kmeans.labels_:
pixel_as_centroid = list(kmeans.cluster_centers_[label])
new_pixels.append(pixel_as_centroid)
new_pixels = np.array(new_pixels).reshape(*ori_img.size, -1)
return new_pixels
new_pixels = replaceWithCentroid(kmeans)
我们的聚类步骤已经完成,让我们看一下压缩图像的结果。
def plotImage(img_array, size):
reload(plt)
plt.imshow(np.array(img_array/255).reshape(*size))
plt.axis('off')
return plt
plotImage(new_pixels, new_pixels.shape).show()

只有两种颜色的压缩图片
K-Means仅使用两种颜色成功地保留了lena.jpg的形状。 在视觉上,我们可以比较原始图像相似与压缩图像是否相似。 但是,我们如何用程序做到这一点? 让我们介绍一组评估压缩图像的指标:
在群集平方和(WCSS)中,测量群集中所有点与其群集中心的欧几里德距离平方的总和。
在群集的平方和(BCSS)之间,测量所有聚类中心之间的欧几里得距离平方的总和。
解释方差,衡量压缩图像效果可以通过压缩图像解释原始图像的百分比。 如果将每个像素视为一个单独的群集,则WCSS等于0。因此,Exparined Variance = 100%。
图像大小,以千字节为单位,以评估缩小/压缩性能。
def calculateBCSS(X, kmeans):
_, label_counts = np.unique(kmeans.labels_, return_counts = True)
diff_cluster_sq = np.linalg.norm(kmeans.cluster_centers_ - np.mean(X, axis = 0), axis = 1)**2
return sum(label_counts * diff_cluster_sq)
WCSS = kmeans.inertia_
BCSS = calculateBCSS(X, kmeans)
exp_var = 100*BCSS/(WCSS + BCSS)
print("WCSS: {}".format(WCSS))
print("BCSS: {}".format(BCSS))
print("Explained Variance: {:.3f}%".format(exp_var))
print("Image Size: {:.3f} KB".format(imageByteSize(new_pixels)))
WCSS: 109260691.314189
BCSS: 193071692.34763986
Explained Variance: 63.861%
Image Size: 4.384 KB
图像大小从86 KB大幅下降到4.384 KB,但是要注意的是,压缩图像解释原始图像的能力达到63.861%。 我们期望比这更高的解释方差百分比。 接下来,我们将重复上述过程并改变𝑘来实现此目标。
重复试验
在本节中,我们将在𝑘= 2到𝑘= 20之间重复此步骤:
- 执行k-means以获取每个像素的聚类中心和聚类标签
- 将每个像素替换为其聚类中心。
- 保存指标值以进行进一步优化:WCSS,BCSS,解释方差和图像大小
- 用越来越多的颜色绘制压缩图像
range_k_clusters = (2, 21)
kmeans_result = []
for k in range(*range_k_clusters):
# CLUSTERING
kmeans = KMeans(n_clusters = k,
n_jobs = -1,
random_state = 123).fit(X)
# REPLACE PIXELS WITH ITS CENTROID
new_pixels = replaceWithCentroid(kmeans)
# EVALUATE
WCSS = kmeans.inertia_
BCSS = calculateBCSS(X, kmeans)
exp_var = 100*BCSS/(WCSS + BCSS)
metric = {
"No. of Colors": k,
"Centroids": list(map(get_colour_name, np.uint8(kmeans.cluster_centers_))),
"Pixels": new_pixels,
"WCSS": WCSS,
"BCSS": BCSS,
"Explained Variance": exp_var,
"Image Size (KB)": imageByteSize(new_pixels)
}
kmeans_result.append(metric)
kmeans_result = pd.DataFrame(kmeans_result).set_index("No. of Colors")
kmeans_result

聚类指标:最佳的颜色种类数
在本节中,我们将尝试搜索最佳的颜色数(聚类中心)k,以便在保持较高的解释方差百分比的同时将内存大小减小到尽可能小。
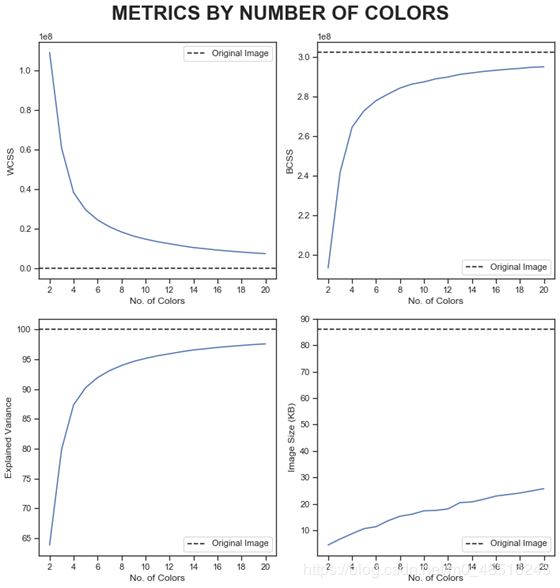
如何确定最佳颜色数k? 以下是算法:
- 用直线连接曲线的第一个和最后一个点
- 计算每个点到该线的垂直距离
- 将距离最长的点视为拐点
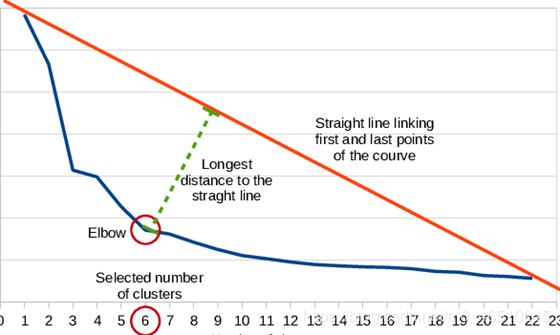
下一个问题,如何在步骤2中计算垂直距离? 很简单,我们可以使用从点(x0,y0)到线ax + by + c = 0的距离公式,如下所示:
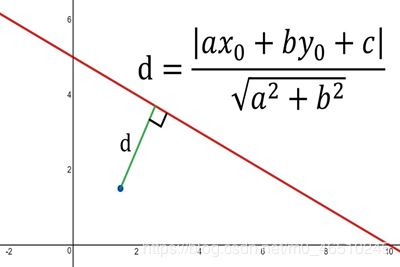
def locateOptimalElbow(x, y): # START AND FINAL POINTS p1 = (x[0], y[0]) p2 = (x[-1], y[-1]) # EQUATION OF LINE: y = mx + c m = (p2[1] - p1[1]) / (p2[0] - p1[0]) c = (p2[1] - (m * p2[0])) # DISTANCE FROM EACH POINTS TO LINE mx - y + c = 0 a, b = m, -1 dist = np.array([abs(a*x0+b*y0+c)/math.sqrt(a**2+b**2) for x0, y0 in zip(x,y)]) return np.argmax(dist) + x[0]
但是,如果图形不是增加或减少的曲线函数,该怎么办? 我们可以使用有限差分法使用二阶导数来定位梯度中变化最剧烈的地方。
什么是有限差分法? 这是一种数值方法,可以近似离散值的导数。 共有三种类型:
forward差异:
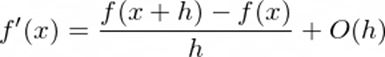
backward差异:
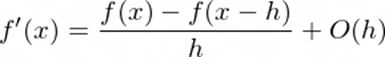
中心差异:
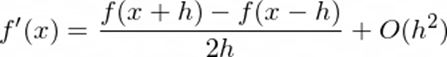
其中:
f'(x)是函数f(x)的一阶导数
h是步长,在这种情况下,h = 1(颜色数的步长)
O(h)是一级误差项
O(h²)是二次误差项
由于中心差异具有较高的度数误差项,因此预期它会比其他两个差异产生更好的结果。 我们仅对第一个点使用前向差异,对最后一个点使用后向差异。
def calculateDerivative(data):
derivative = []
for i in range(len(data)):
if i == 0:
# FORWARD DIFFERENCE
d = data[i+1] - data[i]
elif i == len(data) - 1:
# BACKWARD DIFFERENCE
d = data[i] - data[i-1]
else:
# CENTER DIFFERENCE
d = (data[i+1] - data[i-1])/2
derivative.append(d)
return np.array(derivative)
def locateDrasticChange(x, y):
# CALCULATE GRADIENT BY FIRST DERIVATIVE
first_derivative = calculateDerivative(np.array(y))
# CALCULATE CHANGE OF GRADIENT BY SECOND DERIVATIVE
second_derivative = calculateDerivative(first_derivative)
return np.argmax(np.abs(second_derivative)) + x[0]
让我们搜索每个指标的最佳k值:
optimal_k = []
for col in kmeans_result.columns[2:]:
optimal_k_dict = {}
optimal_k_dict["Metric"] = col
if col == "Image Size (KB)":
optimal_k_dict["Method"] = "Derivative"
optimal_k_dict["Optimal k"] = locateDrasticChange(kmeans_result.index, kmeans_result[col].values)
else:
optimal_k_dict["Method"] = "Elbow"
optimal_k_dict["Optimal k"] = locateOptimalElbow(kmeans_result.index, kmeans_result[col].values)
optimal_k.append(optimal_k_dict)
optimal_k = pd.DataFrame(optimal_k)
optimal_k
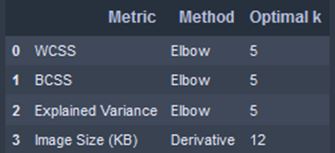
我们选择最大的最优k作为所有最优k的代表,即k = 12。
与原始图像进行比较
最后,让我们比较使用k = 12的压缩图像和原始图像的区别。

relative_size = ori_vs_kmeans.loc["Color-Reduced", "Image Size (KB)"]/ori_vs_kmeans.loc["Original", "Image Size (KB)"]
print("Reduction: {:.3f}% from original image size".format((1-relative_size)*100))
print("Explained Variance: {:.3f}%".format(ori_vs_kmeans.loc["Color-Reduced", "Explained Variance"]))
缩小比例:原始图像的79.012%
解释方差:95.916%
通过使用k-means,我们可以将图像大小减少79.012%,而解释方差为95.916%,这真是太好了! 接下来,我们执行PCA,看看它是否可以优于k-means。
主成分分析(PCA)
概念
PCA是用于降维的无监督学习技术之一。 它从协方差矩阵计算出特征向量,然后将其称为主轴,并按称为解释方差百分比的特征值进行递减排序。 然后将数据集居中并投影到形成主要成分(或分数)的主轴上。 为了减少数据维度,我们仅保留一定数量的主成分n来解释原始数据集的方差,而忽略其余部分。
假设我们有一个X_ori数据集,其中包含m个观察值和n个特征。 减去每行的平均值,我们得到居中的数据X。然后,PCA将为每个特征计算k个特征向量,从而产生形状为n×k的矩阵V。 PCA投影或分数将以Z = XV给出,其中Z的尺寸为m×k。
降维时,我们在X_ori中选择n_select小于n。 以下是我们使用所选PC重建矩阵X的方法:
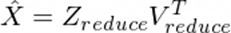
其中:
Z_reduce的尺寸为m×n_select
V_reduce的维数为n×n_select
T是矩阵转置运算
最后,我们添加均值以得到原始图像的最终PCA,如下所示:
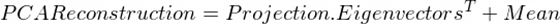
理念
我们将通过选择要使用的主分量n_select利用PCA来减小图像尺寸,以便它仅存储重要像素以保留原始图像的特征,从而使其在存储中更加有效。
我们的原始图像包含三个颜色通道:红色,绿色和蓝色。 对于每个颜色通道,我们将像素视为具有(高度)观察值和(宽度)特征的2D矩阵。 在lena.jpg中,我们有三个2D矩阵,其中包含220个观测值和220个特征。
RGB通道的主要组件
在每个颜色通道上执行PCA,从而得到PCA投影(或分数)和主成分(轴),它们都将是形状为220×220的矩阵形式。
res = []
cum_var = []
X_t = np.transpose(X)
for channel in range(3):
# SEPARATE EACH RGB CHANNEL
pixel = X_t[channel].reshape(*ori_pixels.shape[:2])
# PCA
pca = PCA(random_state = 123)
pixel_pca = pca.fit_transform(pixel)
pca_dict = {
"Projection": pixel_pca,
"Components": pca.components_,
"Mean": pca.mean_
}
res.append(pca_dict)
# EVALUATION
cum_var.append(np.cumsum(pca.explained_variance_ratio_))
我们可以可视化每个颜色通道的主要成分,如下所示:
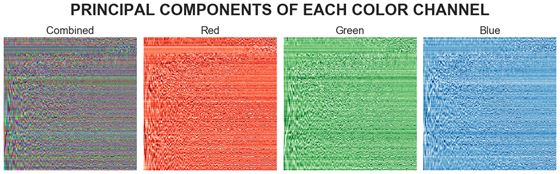
PC的可视化信息不足,随机性很大。 我们应该引入一个称为解释方差的指标来评估PC性能。 取值范围是0到100%,表示原始图像和压缩图像之间的相似度。
cum_var_df = pd.DataFrame(np.array(cum_var).T * 100,
index = range(1, pca.n_components_+1),
columns = ["Explained Variance by Red",
"Explained Variance by Green",
"Explained Variance by Blue"])
cum_var_df["Explained Variance"] = cum_var_df.mean(axis = 1)
cum_var_df
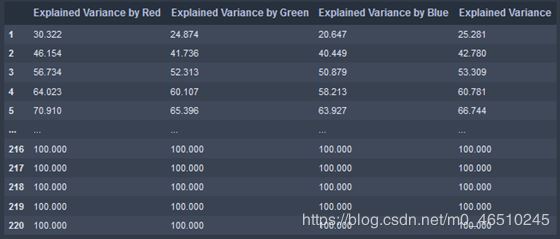
重复试验
在本节中,我们将重复以下步骤从n_select到n_select = 220:
- 区分PCA投影的前n_select列和组件的前n_select行
- 使用PCA建立公式和原始图像
- 对红色,绿色和蓝色每个颜色通道重复步骤1-2。
- 将三种颜色通道的PCA重构组合为一个3D矩阵
- 保存指标值(解释方差,图像大小和颜色数量)以进行进一步优化
- 用越来越多的主成分绘制压缩(重构)图像
pca_results = []
for n in range(1, pca.n_components_+1):
# SELECT N-COMPONENTS FROM PC
temp_res = []
for channel in range(3):
pca_channel = res[channel]
pca_pixel = pca_channel["Projection"][:, :n]
pca_comp = pca_channel["Components"][:n, :]
pca_mean = pca_channel["Mean"]
compressed_pixel = np.dot(pca_pixel, pca_comp) + pca_mean
temp_res.append(compressed_pixel.T)
compressed_image = np.transpose(temp_res)
pca_dict = {
"n": n,
"Pixels": compressed_image,
"Explained Variance": cum_var_df["Explained Variance"][n],
"Image Size (KB)": imageByteSize(compressed_image),
"No. of Colors": len(np.unique(np.uint8(compressed_image).reshape(-1, 3), axis = 0))
}
pca_results.append(pca_dict)
pca_results = pd.DataFrame(pca_results).set_index("n")
pca_results.head()

PCA指标:主成分的最佳数量
在本节中,我们将尝试搜索最佳数量的PC,以在达到预期的解释方差的同时,使内存占用尽可能最小。
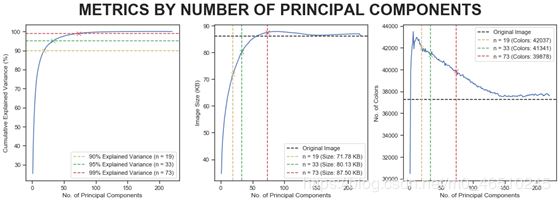
我们想通过分析解释方差来获得最佳主成分数,这是思考过程:
左图:我们需要19、33和73个主成分才能分别解释原始图像的方差的90%,95%和99%。
中图:但是需要权衡取舍,解释方差越大,图像尺寸就越大。 黑色虚线表示原始图像尺寸,我们要在此线下方选择n。 因此,选择19或33个主成分。
右图:如果将n从19增加到33,然后再增加到73,则图像中存在的颜色数量将减少。
从图中可以得出结论,应当33个主成分,因为它给我们提供了较小的图像大小和相当高的解释方差,并且比使用19个主要成分更接近原始图像。
与原始图像进行比较
最后,让对压缩图像和原始图像进行比较。

relative_size = ori_vs_pca.loc["PC-Reduced", "Image Size (KB)"]/ori_vs_kmeans.loc["Original", "Image Size (KB)"]
print("Reduction: {:.3f}% from original image size".format((1-relative_size)*100))
print("Explained Variance: {:.3f}%".format(ori_vs_pca.loc["PC-Reduced", "Explained Variance"]))
缩小比例:原始图像大小的6.825%
解释方差:95.072%
通过使用PCA,我们只能将图像大小减小6.825%,并且压缩后的图像成功捕获了原始图像的95.072%的特征。 接下来,我们比较k-means和PCA的结果。
k-means和PCA的比较
我们考虑几个指标,以比较使用k-means和PCA压缩图像的效果:
图片大小(以千字节为单位)解释方差图像中存在的颜色数
reduction_kmeans = (1-final_compare.loc["Color-Reduced", "Image Size (KB)"] / ori_img_size) * 100
reduction_pca = (1-final_compare.loc["PC-Reduced", "Image Size (KB)"] / ori_img_size) * 100
print("Image Size Reduction using K-Means: {:.3f}%".format(reduction_kmeans))
print("Image Size Reduction using PCA: {:.3f}%".format(reduction_pca))

使用k-means缩小图像大小:79.012%
使用PCA缩小图像大小:6.825%
结论
我们使用无监督学习算法成功地实现了图像压缩,例如k-means聚类和使用主成分分析(PCA)进行降维。
在k-means中,通常通过可视化来主观地选择最佳聚类中心数k。 在这里,我们提出两种选择方法,即:
- 使用最长垂直距离的方法
- 使用有限差分法和二阶导数
在PCA中,确定使用的PC数量首先要考虑解释方差,然后还要考虑图像大小减小的比例和减少颜色的数量,以分析它们与原始图像的相似性。
使用k-means,图像大小减小到79.012%,仅12种颜色就能解释原始图像的95.916%差异。 使用PCA,图像大小减小仅为6.825%,并根据我们的目标解释了95,072%的差异。 在经过PCA缩小的图像中,与原始图像相比,存在更多的颜色数量,表明存在噪音。 从主观上可以看出,PCA压缩的图像更加粗糙。
与PCA相比,更建议使用k-means来缩小图像尺寸,但是如果我们要保持原始图像的整体色彩,请使用PCA。
另一个建议是尝试连续执行两种方法来进行图像缩小,即先用k-means再用PCA,或是先用PCA再用k-means。
作者:Tomy Tjandra
deephub翻译组:孟翔杰
加载全部内容