R语言ARMA模型参数 R语言ARMA模型的参数选择说明

AR(p)模型与MA(q)实际上是ARMA(p,q)模型的特例。它们都统称为ARMA模型，而ARMA（p,q）模型的统计性质也是AR（p）与MA（q）模型的统计性质的有机组合。

平稳系列建模

假如某个观察值序列通过序列预处理可以判定为平稳非白噪声序列，就可以利用ARMA模型对序列建模。

1.求出该观察值序列的样本自相关系数（ACF）与偏相关系数（PACF的值。

2.根据根样本自相关系数和偏自相关系数的性质，选择阶数适当的ARMA（p,q）模型进行拟合。

3.估计模型中未知参数的值

4.检验模型的有效性。如果拟合模型未通过检验，回到步骤（2）,重新选择模型拟合。

5.模型优化。如果拟合模型通过检验，仍然回到步骤（2），充分考虑各种可能，建立多个拟合模型，从所有通过检验的拟合的模型中选择最优模型。

6.利用拟合模型，预测序列将来的走势。

选择合适的模型拟合1950-2008年我国邮路及农村投递线路每年新增里程数序列：

白噪声检验：

 for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag=6*i))
    Box-Ljung test
data:  x
X-squared = 37.754, df = 6, p-value = 1.255e-06
    Box-Ljung test
data:  x
X-squared = 44.62, df = 12, p-value = 1.197e-05

绘制自相关图和偏自相关图

acf(x)
pacf(x)

补充：关于ARMA模型的R语言实现

新手一枚，和大家一起学习R，以后基本每周都会更新1到2篇关于数据预测处理的模型和方法，希望和大家一起学习，一起成长。

本周首先更新的是用R来实现ARMA模型。

时间序列的模型，基本上都要建立在平稳的序列上，这里我们将来了解下ARMA模型，以及其实现的R代码。

ARMA（p,q)模型，全称移动平均自回归模型，它是由自回归（AR）部分和移动平均（MA）部分组成的，所以称之为ARMA模型。进行ARMA模型的话，要求时间序列一定要是平稳的才行，否则建模无效。

1.ARMA模型具有如下形式：

2.ARMA模型建模步骤

(1)画出时序图，求出样本的相关系数，偏自相关系数值

(2)根据样本的相关系数和偏自相关系数，选择适当的阶数，由于这具有一定的主观性，所以这里我们选用的是最小AIC准则来定阶

(3)估计模型中的参数值

(4)检验模型的有效性，一般分为残差的白噪声检验和参数的显著性检验。

(5)利用模型进行预测。

3.建模

我们利用美国科罗拉多州某一加油站连续57天的OVERSHOOT序列,来进行本次建模。

（1）首先

读入数据，画出其时序图，检验其平稳性。

library(zoo)
library(tseries)
library(forecast)
overshort=read.table("C:/Users/MrDavid/data_TS/A1.9.csv",sep=",",header=T)
overshort=ts(overshort)
plot(overshort,col=4,lwd=2,pch=8,type="o")

结果如下：

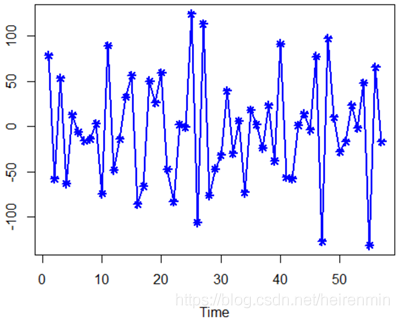
进行一次单位根检验，测试该序列的平稳性：

代码：adf.test(overshort)

结果如下图所示：

由以上单位根检验，我们看到P值为0.01小于0.05，所以该序列平稳

（2）对于平稳的时间序列

我们需要进行白噪声检验，因为白噪声是纯随机序列，对白噪声序列进行建模毫无意义。

for(i in 1:3) print(Box.test(overshort,type="Ljung-Box",lag=6*i))

结果如下图：

可以看出，该序列非白噪声序列，可以进行建模。

（3）模型的拟合

模型的拟合，我们可以画出自相关图，和偏自相关图，对时间序列进行定阶

acf(overshort,col=4,lwd=2)
pacf(overshort,col=4,lwd=2)

结果如下：

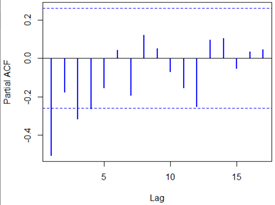
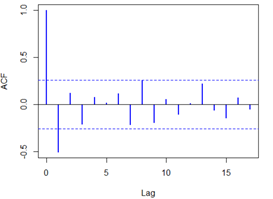
自相关图除了显示1阶延迟在两倍标准差之外，其他自相关系数都在两倍标准差之内，可以认为该序列自相关系数1阶截尾，骗子相关系数显示出非截尾性质，可以拟合模型为ARMA(0,1)，即MA(1)模型。

该模型除了自相关，偏自相关系数定阶以外，还可以根据自动定阶函数auto.arima来对该序列进行定阶结果如下：

auto.arima(overshort)

也显示出该序列的模型为MA(1)模型

接下来进行建模，找出模型的系数：

a=arima(overshort,order=c(0,0,1),include.mean=T)
a

得出结果：

该模型为：

对模型进行显著性检验：

for(i in 1:3) print(Box.test(a$residual,type="Ljung-Box",lag=6*i))

残差的白噪声检验，反映出，该残差是白噪声序列，所以残差白噪声检验通过。

对参数进行显著性检验：

t1=-0.8477/0.1206
pt(t1,df=12,lower.tail=T)
t2=-4.7945/1.0252
pt(t2,df=12,lower.tail=T)

参数的显著性检验也通过，说明该序列建模成功。

（4）利用该模型预测未来5期值。

a.fore=forecast(a,h=5)
a.fore

（5）画出预测图：

L1=a.fore$fitted-1.96*sqrt(a$sigma2)
U1=a.fore$fitted+1.96*sqrt(a$sigma2)
L2=ts(a.fore$lower[,2])
U2=ts(a.fore$upper[,2])
c1=min(overshort,L1,L2)
c2=max(overshort,L2,U2)
plot(overshort,type="p",pch=8,ylim=c(c1,c2))
lines(a.fore$fitted,col=2,lwd=2)
lines(a.fore$mean,col=2,lwd=2)
lines(L1,col=4,lty=2)
lines(U1,col=4,lty=2)
lines(L2,col=4,lty=2)
lines(U2,col=4,lty=2)

以上为个人经验，希望能给大家一个参考，也希望大家多多支持。如有错误或未考虑完全的地方，望不吝赐教。