基于sinc的音频重采样（二）：实现

上篇（基于sinc的音频重采样（一）：原理）讲了基于sinc方法的重采样原理，并给出了数学表达式，如下：

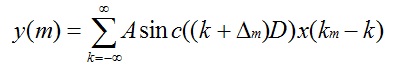                                                                                (1)

本文讲如何基于这个数学表达式来做软件实现。软件实现的细节很多，这里主要讲核心部分。函数srcUD()和filterUD()就是实现的主要函数（这两个函数是在源码基础上作了一定的改动，核心思想没变）。srcUD()是实现一帧中点的重采样，一个点一个点的做。filterUD()被srcUD()调用。数学表达式就体现在函数filterUD()里。粗看肯定会懵，怎么也跟上面的数学表达式联系不起来。下面就讲讲实现细节，让代码和数学表达式联系起来。

 

先看函数srcUD( )，下图是其实现，是将一帧中原采样点的值转换成新的采样率下的值，图中对输入参数的意思已做了解释。

 

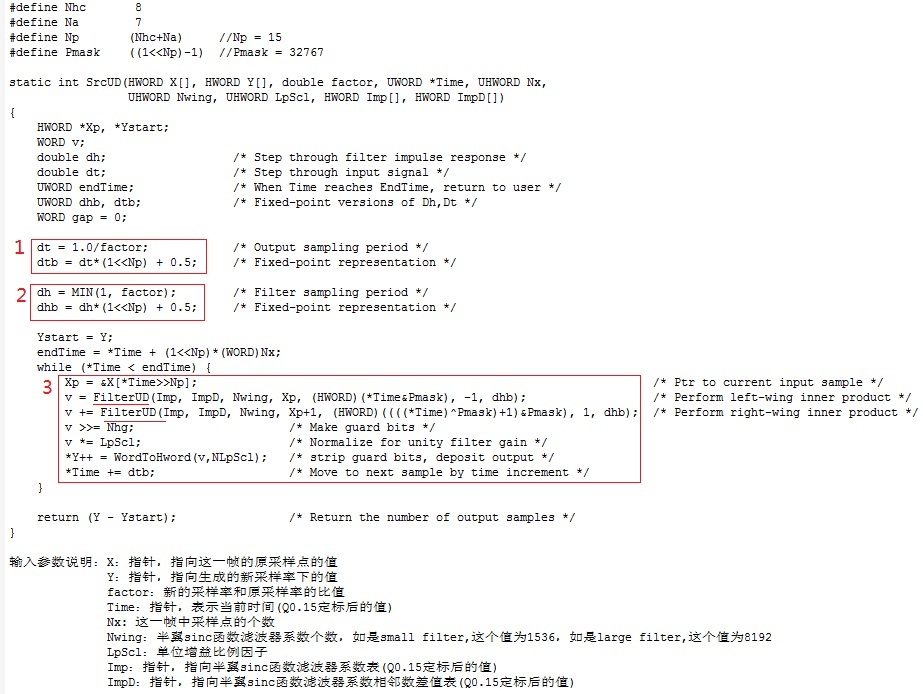
主要看3个细节。标1的红框处是算新的采样率下两个点之间的采样间隔。设定Tx为原采样率下的采样间隔，Ty为新的采样率下的采样间隔，factor = Tx / Ty，所以 Ty = Tx / factor。软件实现时对采样间隔做归一化处理，设定Tx = 1，即原采样点x(n)的采样间隔归一化到1，则新采样点y(m)的采样间隔为Ty = 1/factor。把采样间隔用Q0.15的定标表示，所以原采样率下的采样间隔为32768，新的采样率下的采样间隔是dtb = dt *(1 << Np) +0.5 (加上0.5是做四舍五入)。标2的红框处是算数学表达式1中的D。D = A = min(1, factor) = 代码中的dh，同dtb，再用Q0.15定标就是dhb。标3的红框处是具体算生成的新采样率下的点的值。这一帧开始时间是*Time，原采样率下采样点间隔已归一化为1，定标后变成了32768，帧内有Nx个点，所以这帧的结束时间是endTime = *Time + (1<<Np)*(WORD)Nx。每生成一个新的采样率下的点后时间就会向后移动一个新的采样率下的采样间隔（即dtb）开始算新的采样点的值，直到时间超过了endTime。算每个新的采样点时先要找到它对应的数学表达式中的x(Km)，即对时间取整，代码中就是Xp = &X[*Time>>Np]，这里Xp就是对应的x(Km)。(*Time&Pmask) 就是算Δm。算重采样后的一个新产生的点的值时，先算左翼(left wing)的值，再算右翼(right wing)的值，然后两个值相加就得到了这个新的采样点的值了。关于左右半翼，下文算sinc函数值时会讲。算左右半翼值的函数是一样的，即filterUD()。先看看怎么把算左右半翼的值用一个函数表示的。回到上面的数学表达式1，假设sinc函数左右都取hend个过零点，上式就变成了

                         

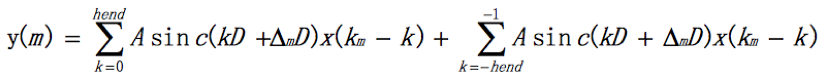
可以看出把计算变成了两部分相加，前半部分是左翼，后半部分是右翼，即：

                                                     

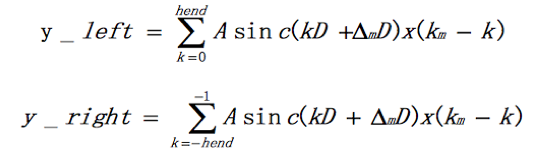
所以y(m) = y_left + y_right。着重看右翼。令i=k+1，则

                                                        

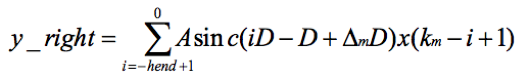
再令i = -i，则

                                                      

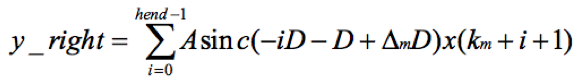
由于sinc函数是偶对称函数，即sinc(-x) = sinc(x)。所以上式变成

                                                    

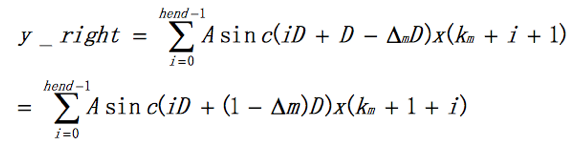
为了公式统一，令 Δ′m= 1 - Δm，i=k，则

                                                        

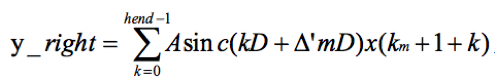
再看y_left的表达式：

                                                       

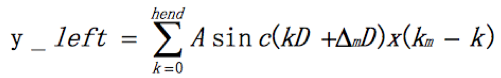
可以看出计算左右两翼的表达式统一了，只是传给函数的参数有差异。

 

再来看函数filterUD( )，下图是其实现，是生成新的采样率下的一个点的半翼的值，图中对输入参数的意思已做了解释。

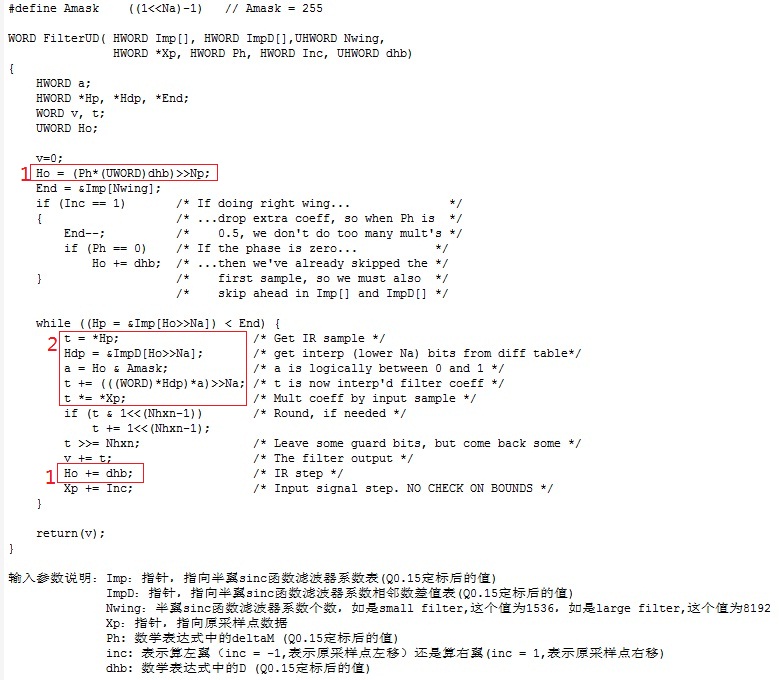
再看上面的数学表达式1。在式子中，有变量Km和Δm，当新旧采样率以及m确定时它们就是已知变量，在原理篇中讲过它们的求法。y(m)是A、sinc((k+Δm)D)和x(k_m - k)的乘累加，A和x(k_m - k)均很容易得到，唯独sinc((k+Δm)D)需要计算求出。下面看怎么求sinc((k+Δm)D)。

 

为了减少计算量，求sinc函数值通常采用查表的方法，即先做好表，使用时根据索引查表得到函数值。sinc函数是连续的，计算机处理时要先变成离散的。sinc函数是偶函数，关于Y轴对称，右半轴（或叫右翼，right wing）的值得到了，左半轴（或叫左翼，left wing）的值也就得到了。这样也就减小了表的大小（表的大小减为一半）。在右翼中，对每个过零点之间做256次采样，就得到了sinc函数值的离散表示。以从0到第一个过零点为例，256均分X轴从0到1的函数值，如下图：

                                                          

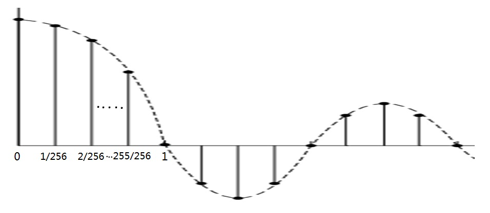
可以根据原理篇中sinc函数的表达式算出每个采用点上的函数值，具体如下：

类似的可以算出右轴的每两个过零点之间的样本的函数值。如果截断后右翼共有6个过零点，则表中共有1536（1536 = 256 * 6）个值，分别为（1，0.99997458，0999989969， ........），把这些值叫做sinc函数滤波器系数。开源实现中分small filter和large filter两个表，两个表中过零点之间均是256采样，但small filter是6个过零点，表中共1536个值，而large filter是32个过零点，表中共8192个值。由于用了更多的sinc函数值和原采用率下的样本值，large filter的效果更好，同时运算量也大好多。具体使用时需要评估用哪个表。

 

sinc函数的表做好了，但是sinc((k+Δm)D)中的(k+Δm)D有可能不落在那些离散的样本上，即(k+Δm)D不等于1/256、2/256等，而是落在两个样点之间，例如落在1/256和2/256之间的蓝点，如下图：

                                                        

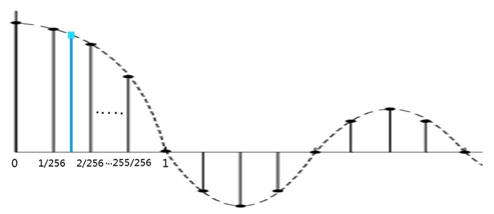
这时的sinc函数值怎么求呢？软件实现中用了线性插值法。线性插值是一种针对一维数据的插值方法，它根据一维数据序列中需要插值的点的左右邻近两个数据点来进行数值的估计。它是根据到这两个点的距离来分配它们的比重的。如下图：

                                                                        

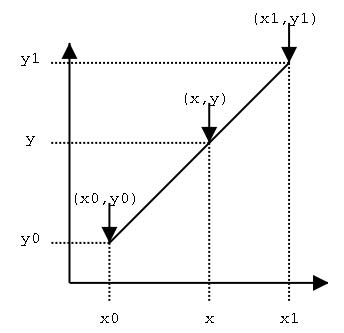
已知点(x0,y0)、(x1,y1)，如果在x处插值，则y的值可用下式求出：

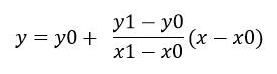                                                                                               （2）

这样sinc函数值就求出来了。

 

算sinc函数值的表是浮点的，为了减少运算时的load，需要将浮点数定点化，即用Q格式表示。用Q0.15给表做定点化，表就变成了（32767，32766，……..），即代码中的数组Imp（实现中也把两个相邻的样本的Y值的差（即2式中的y1-y0）做成了表，即数组ImpD。这样处理减少了运算，属于典型的用空间换时间）。相应的其他浮点数的值也要做定点化，如Δm。sinc的横轴值x也要做定点化，也是用的Q0.15，这样第一个过零点的值定点化后就变为了32768。sinc函数两个过零点之间共256个样本，所以样本的间隔是128（32768 / 256 = 128），即2式中的x1-x0的值。x除以128(即右移7位)就可算出落在哪两个样本之间。x & 128表示与相邻左样本的距离，即2式中的x-x0的值。y0也是定点化后的值，根据2式，落在两个样本之间的sinc的定点化后的值也就得到了。

 

现在看代码中的实现细节。标1的红框处是算Δm*D（Ho = (Ph*(UWORD)dhb)>>Np）以及每次加上D后的值（Ho += dhb）。不管是算左翼还是右翼的值，从表达式看出k都是从0开始，所以sinc(k*D + Δm*D)的第一个值是sinc(Δm*D)，即k=0时的值Ho。后面经过一个原采样点，即k加1，Ho就会加上D(即dhb)得到一个新的k*D + Δm*D。标2的红框处，Ho>>Na（即Ho右移7位）可知落在哪两个sinc样本之间，*Hp = Imp[Ho>>Na]表示左边的样本的值，即表达式2中的y0的值。同样*Hdp = ImpD[Ho>>Na]表示左右两边样本的差值，即表达式2中的y1-y0的值。a = Ho & Amask 表示与相邻左样本的距离，即x-x0。上面说过定标后两个样本之间的间隔是128，即x1-x0的值是128，代码中表现出来就是右移7位（>>Na）。所以(*Hdp)*a)>>Na就表示(y1-y0)*(x-x0)/(x1-x0)。t = *Hp表示想要求的值左边的样本，即y0，因而t += (((WORD)*Hdp)*a)>>Na就是实现了表达式2，sinc函数值就求出来了。再乘以相对应的原采样点（即t *= *Xp）就得到了sinc(k*D + Δm*D)*x(km -k)的值。算好一个值后Ho会加上D，原采样点也会左移或右移一个，从而算下一个值，直到sinc样本的结束处。把这些算好的值加起来就是半翼的值了，再把左右半翼的值加起来就得到了新采样率下的一个点的值了。

 

把函数srcUD()和filterUD()搞明白了基于sinc重采样的软件实现就好理解了。