java二叉搜索树利用java实现二叉搜索树

时间:2021-04-16 \(^o^)/kūn 人气:0

想了解利用java实现二叉搜索树的相关内容吗，\(^o^)/kūn在本文为您仔细讲解java二叉搜索树的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：java二叉搜索树,java二叉树，下面大家一起来学习吧。

二叉搜索树的定义

它是一颗二叉树
任一节点的左子树上的所有节点的值一定小于该节点的值
任一节点的右子树上的所有节点的值一定大于该节点的值

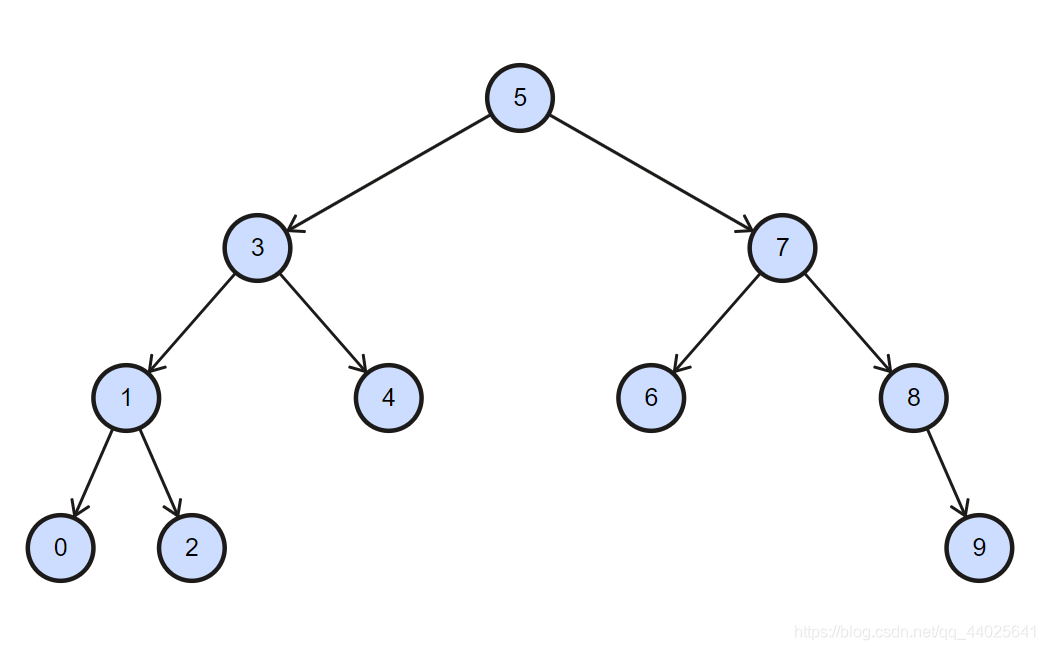
二叉排序树

特点： 二叉搜索树的中序遍历结果是有序的（升序）！

实现一颗二叉搜索树

实现二叉搜索树，将实现插入，删除，查找三个方面
二叉搜索树的节点是不可以进行修改的，如果修改，则可能会导致搜索树的错误

二叉搜索树的定义类

二叉搜索树的节点类 —— class Node
二叉搜索树的属性：要找到一颗二叉搜索树只需要知道这颗树的根节点。

public class BST {
    static class Node {
        private int key;
        private Node left;
        private Node right;

        public Node(int key) {
            this.key = key;
        }
    }

    private Node root;//BST的根节点
}

二叉搜索树的查找

二叉搜索树的查找思路：
①如果要查找的值等于当前节点的值，那么，就找到了
②如果要查找的值小于当前节点的值，那么，就往当前节点的左子树走
③如果要查找的值大于当前节点的值，那么，就往当前节点的右子树走
最终，如果走到空了还没有找到，就说明不存在这个key

/**
 * 查找是否存在节点
 *
 * 思路：根据二叉排序树的特点：
 * ①如果要查找的值小于当前节点的值，那么，就往当前节点的左子树走
 * ②如果要查找的值大于当前节点的值，那么，就往当前节点的右子树走
 *
 * @param key 带查找的key
 * @return boolean是否存在
 */
public boolean find(int key) {
	Node cur = root;
	while (cur != null) {
		if (key < root.key) {
			cur = cur.left;
		} else if (key > root.key) {
			cur = cur.right;
		} else {
			return true;
		}
	}
	return false;
}

二叉搜索树的插入

二叉搜索树的插入思路：
思路和查找一样的，只是我们这次要进行的是插入操作，那么我们还需要一个parent节点，来时刻记录当前节点的双亲节点即：
①如果要插入的值等于当前节点的值，那么，无法插入（不可出现重复的key）
②如果要插入的值小于当前节点的值，那么，就往当前节点的左子树走
③如果要插入的值大于当前节点的值，那么，就往当前节点的右子树走
最终，如果走到空了，就说明不存在重复的key，只要往双亲节点的后面插就好了，就是合适的位置，具体往左边还是右边插入，需要比较待插入节点的key和parent的key

/**
 * 往二叉树中插入节点
 *
 * 思路如下：
 *
 * @param key 待插入的节点
 */
public void insert(int key) {
	if (root == null) { //如果是空树，那么，直接插入
		root = new Node(key);
		return;
	}

	Node cur = root;
	Node parent = null; //parent 为cur的父节点
	while (true) {
		if (cur == null) { //在遍历过程中，找到了合适是位置，就指针插入（没有重复节点）
			if (parent.key < key) {
				parent.right = new Node(key);
			} else {
				parent.left = new Node(key);
			}
			return;
		}

		if (key < cur.key) {
			parent = cur;
			cur = cur.left;
		} else if (key > cur.key) {
			parent = cur;
			cur = cur.right;
		} else {
			throw new RuntimeException("插入失败，已经存在key");
		}
	}
}

二叉搜索树的删除

二叉搜索树的删除思路：（详细的思路看注释）
首先，需要先找到是否存在key节点，如果存在，则删除，如果不存在则删除错误
对于，如果存在，则分为三种情况：
①要删除的节点，没有左孩子

Ⅰ：要删除的节点为根节点：root = delete.right;
Ⅱ：要删除的节点为其双亲节点的左孩子：parent.left = delete.right;
Ⅲ：要删除的节点为其双亲节点的右孩子：parent.right = delete.right;

②要删除的节点，没有右孩子

Ⅰ：要删除的节点为根节点：root = delete.left;
Ⅱ：要删除的节点为其双亲节点的左孩子：parent.left = delete.left;
Ⅲ：要删除的节点为其双亲节点的右孩子：parent.right = delete.left;

③要删除的节点，既有左孩子又有右孩子：

此时我们需要找到整颗二叉树中第一个大于待删除节点的节点，然后替换他俩的值，最后，把找到的节点删除
Ⅰ：找到的节点的双亲节点为待删除的节点：delete.key = find.key; findParent.right = find.right;
Ⅱ：找到的节点的双亲节点不是待删除的节点：delete.key = find.key; findParent.left = find.right;

/**
 * 删除树中节点
 *
 * 思路如下：
 *
 * @param key 待删除的节点
 */
public void remove(int key) {
	if (root == null) {
		throw new RuntimeException("为空树，删除错误！");
	}
	Node cur = root;
	Node parent = null;
	//查找是否key节点的位置
	while (cur != null) {
		if (key < cur.key) {
			parent = cur;
			cur = cur.left;
		} else if (key > cur.key) {
			parent = cur;
			cur = cur.right;
		} else {
			break;
		}
	}
	if (cur == null) {
		throw new RuntimeException("找不到key，输入key不合法");
	}

	//cur 为待删除的节点
	//parent 为待删除的节点的父节点
	/*
         * 情况1：如果待删除的节点没有左孩子
         * 其中
         * ①待删除的节点有右孩子
         * ②待删除的节点没有右孩子
         * 两种情况可以合并
         */
	if (cur.left == null) {
		if (cur == root) { //①如果要删除的是根节点
			root = cur.right;
		} else if (cur == parent.left) { //②如果要删除的是其父节点的左孩子
			parent.left = cur.right;
		} else { //③如果要删除的节点为其父节点的右孩子
			parent.right = cur.right;
		}
	}
	/*
         * 情况2:如果待删除的节点没有右孩子
         *
         * 其中:待删除的节点必定存在左孩子
         */
	else if (cur.right == null) { //①如果要删除的是根节点
		if (cur == root) {
			root = cur.left;
		} else if (cur == parent.left) { //②如果要删除的是其父节点的左孩子
			parent.left = cur.left;
		} else { //③如果要删除的节点为其父节点的右孩子
			parent.right = cur.left;
		}
	}
	/*
        * 情况3:如果待删除的节点既有左孩子又有右孩子
        *
        * 思路:
        * 因为是排序二叉树,要找到整颗二叉树第一个大于该节点的节点,只需要,先向右走一步,然后一路往最左走就可以找到了
        * 因此:
        * ①先向右走一步
        * ②不断向左走
        * ③找到第一个大于待删除的节点的节点,将该节点的值,替换到待删除的节点
        * ④删除找到的这个节点
        * ⑤完成删除
        *
         */
	else {
		Node nextParent = cur; //定义父节点,初始化就是待删除的节点
		Node next = cur.right; //定义next为当前走到的节点,最终目的是找到第一个大于待删除的节点
		while (next.left != null) {
			nextParent = next;
			next = next.left;
		}
		cur.key = next.key; //找到之后,完成值的替换
		if (nextParent == cur) { //此时的父节点就是待删除的节点,那么说明找到的节点为父节点的右孩子(因为此时next只走了一步)
			nextParent.right = next.right;
		} else { //此时父节点不是待删除的节点,即next确实往左走了,且走到了头.
			nextParent.left = next.right;
		}
	}

}

加载全部内容

java二叉搜索树 利用java实现二叉搜索树