pytorch多项式回归 pytorch实现多项式回归
逝去〃年华 人气:0想了解pytorch实现多项式回归的相关内容吗,逝去〃年华在本文为您仔细讲解pytorch多项式回归的相关知识和一些Code实例,欢迎阅读和指正,我们先划重点:pytorch,多项式回归,下面大家一起来学习吧。
pytorch实现多项式回归,供大家参考,具体内容如下
一元线性回归模型虽然能拟合出一条直线,但精度依然欠佳,拟合的直线并不能穿过每个点,对于复杂的拟合任务需要多项式回归拟合,提高精度。多项式回归拟合就是将特征的次数提高,线性回归的次数使一次的,实际我们可以使用二次、三次、四次甚至更高的次数进行拟合。由于模型的复杂度增加会带来过拟合的风险,因此需要采取正则化损失的方式减少过拟合,提高模型泛化能力。希望大家可以自己动手,通过一些小的训练掌握pytorch(案例中有些观察数据格式的代码,大家可以自己注释掉)
# 相较于一元线性回归模型,多项式回归可以很好的提高拟合精度,但要注意过拟合风险
# 多项式回归方程 f(x) = -1.13x-2.14x^2+3.12x^3-0.01x^4+0.512
import torch
import matplotlib.pyplot as plt
import numpy as np
# 数据准备(测试数据)
x = torch.linspace(-2,2,50)
print(x.shape)
y = -1.13*x - 2.14*torch.pow(x,2) + 3.15*torch.pow(x,3) - 0.01*torch.pow(x,4) + 0.512
plt.scatter(x.data.numpy(),y.data.numpy())
plt.show()
# 此时输入维度为4维
# 为了拼接输入数据,需要编写辅助数据,输入标量x,使其变为矩阵,使用torch.cat拼接
def features(x): # 生成矩阵
# [x,x^2,x^3,x^4]
x = x.unsqueeze(1)
print(x.shape)
return torch.cat([x ** i for i in range(1,5)], 1)
result = features(x)
print(result.shape)
# 目标公式用于计算输入特征对应的标准输出
# 目标公式的权重如下
x_weight = torch.Tensor([-1.13,-2.14,3.15,-0.01]).unsqueeze(1)
b = torch.Tensor([0.512])
# 得到x数据对应的标准输出
def target(x):
return x.mm(x_weight) + b.item()
# 新建一个随机生成输入数据和输出数据的函数,用于生成训练数据
def get_batch_data(batch_size):
# 生成batch_size个随机的x
batch_x = torch.randn(batch_size)
# 对于每个x要生成一个矩阵
features_x = features(batch_x)
target_y = target(features_x)
return features_x,target_y
# 创建模型
class PolynomialRegression(torch.nn.Module):
def __init__(self):
super(PolynomialRegression, self).__init__()
# 输入四维度 输出一维度
self.poly = torch.nn.Linear(4,1)
def forward(self, x):
return self.poly(x)
# 开始训练模型
epochs = 10000
batch_size = 32
model = PolynomialRegression()
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(),0.001)
for epoch in range(epochs):
print("{}/{}".format(epoch+1,epochs))
batch_x,batch_y = get_batch_data(batch_size)
out = model(batch_x)
loss = criterion(out,batch_y)
optimizer.zero_grad()
loss.backward()
# 更新梯度
optimizer.step()
if (epoch % 100 == 0):
print("Epoch:[{}/{}],loss:{:.6f}".format(epoch,epochs,loss.item()))
if (epoch % 1000 == 0):
predict = model(features(x))
print(x.shape)
print(predict.shape)
print(predict.squeeze(1).shape)
plt.plot(x.data.numpy(),predict.squeeze(1).data.numpy(),"r")
loss = criterion(predict,y)
plt.title("Loss:{:.4f}".format(loss.item()))
plt.xlabel("X")
plt.ylabel("Y")
plt.scatter(x,y)
plt.show()
拟合结果:
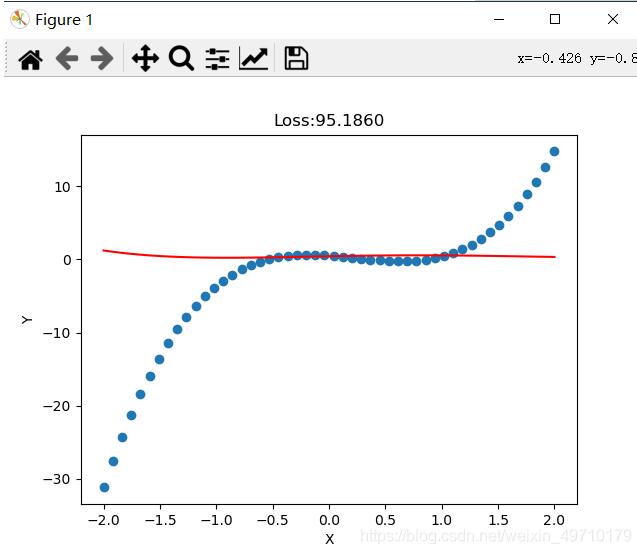
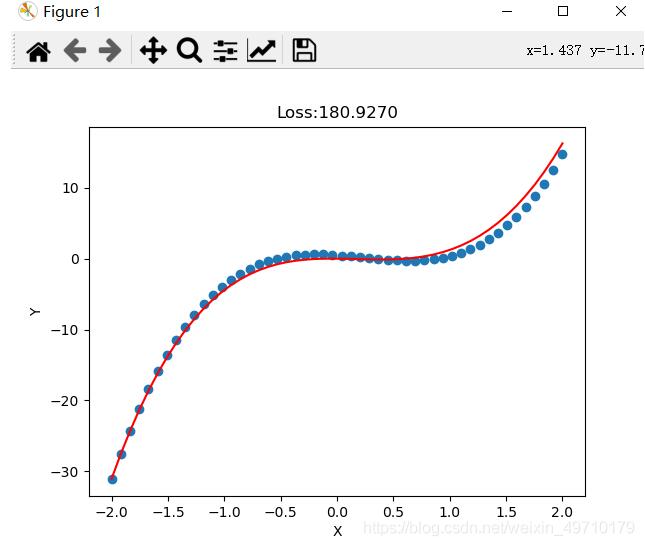
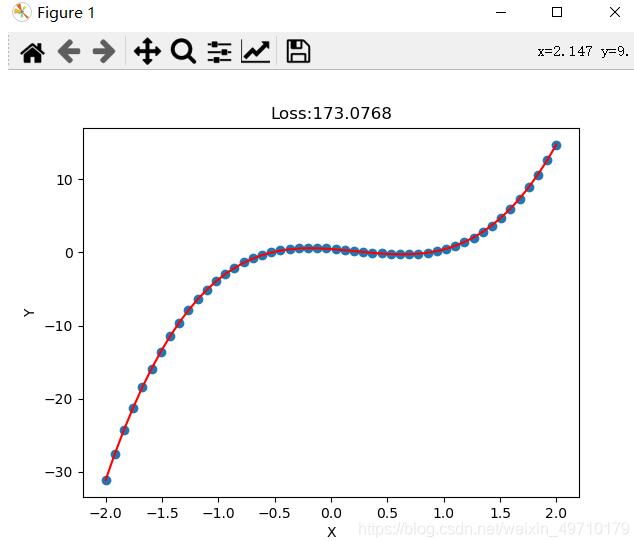
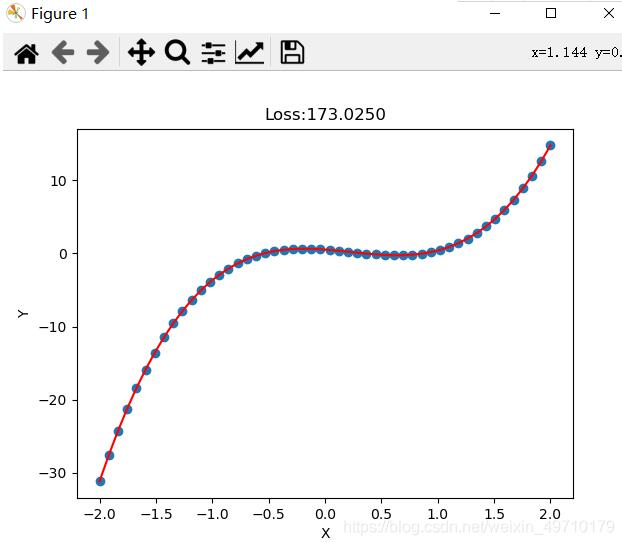
加载全部内容