Opencv实现最小外接矩形和圆

时间:2021-04-03 人气:0

步骤：将一幅图像先转灰度，再canny边缘检测得到二值化边缘图像，再寻找轮廓，轮廓是由一系列点构成的，要想获得轮廓的最小外接矩形，首先需要得到轮廓的近似多边形，用道格拉斯-普克抽稀（DP）算法，道格拉斯-普克抽稀算法，是将曲线近似表示为一系列点，并减少点的数量的一种算法。

该算法实现抽稀的过程是：

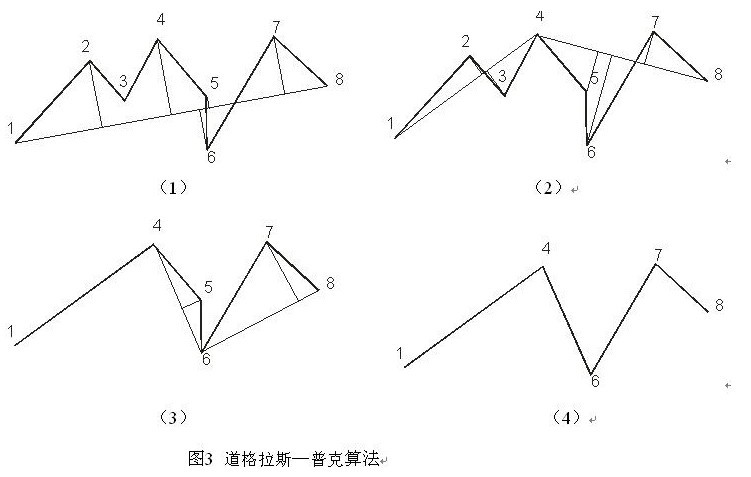
1）对曲线的首末点虚连一条直线，求曲线上所有点与直线的距离，并找出最大距离值dmax，用dmax与事先给定的阈值D相比：
2）若dmax<D，则将这条曲线上的中间点全部舍去；则该直线段作为曲线的近似，该段曲线处理完毕。

若dmax≥D，保留dmax对应的坐标点，并以该点为界，把曲线分为两部分，对这两部分重复使用该方法，即重复1），2）步，直到所有dmax均<D，即完成对曲线的抽稀。

#include<opencv2/opencv.hpp>
using namespace cv;
using namespace std;
 
int value = 60;
RNG rng(1);
Mat src,gray_img,canny_img,dst;
void callback(int, void*);
int main(int arc, char** argv){ 
 src = imread("2.jpg"); 
 namedWindow("input",CV_WINDOW_AUTOSIZE);
 imshow("input", src);
 cvtColor(src, gray_img, CV_BGR2GRAY);
 namedWindow("output", CV_WINDOW_AUTOSIZE);
 createTrackbar("threshold", "output", &value, 255, callback);
 callback(0, 0);
 waitKey(0);
 return 0;
}
void callback(int, void*) { 
 Canny(gray_img, canny_img, value, 2 * value);
 
 vector<vector<Point>>contours;
 vector<Vec4i> hierarchy;
 findContours(canny_img, contours, hierarchy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE, Point(0, 0));
 
 vector<vector<Point>> contours_poly(contours.size());
 vector<Rect>poly_rects(contours.size());
 vector<Point2f>ccs(contours.size());
 vector<float>radius(contours.size());
 
 vector<RotatedRect> minRects(contours.size());
 vector<RotatedRect> myellipse(contours.size());
 
 for (int i = 0; i < contours.size(); i++) {
 approxPolyDP(contours[i], contours_poly[i], 20, true);//获得点数比较少的近似多边形
 poly_rects[i] = boundingRect(contours_poly[i]);//从近似多边形获得最小外接矩形
 minEnclosingCircle(contours_poly[i], ccs[i], radius[i]);//从近似多边形获得最小外接圆
 //多边形点数大于5才能绘制带方向的最小矩形和椭圆
 if (contours_poly[i].size() > 5) {
 minRects[i] = minAreaRect(contours_poly[i]);//从近似多边形获得带方向的最小外接矩形
 myellipse[i] = fitEllipse(contours_poly[i]);//从近似多边形获得带方向的最小外接椭圆
 } 
 }
 
 //绘制
 src.copyTo(dst);
 Point2f pts[4];
 for (int j = 0; j < contours.size(); j++) {
 Scalar color = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255));
 rectangle(dst, poly_rects[j], color, 2,8);
 circle(dst, ccs[j], (int)radius[j], color, 2,8);
 
 //绘制带方向的最小外接矩形和椭圆
 if (contours_poly[j].size() > 5) {
 ellipse(dst, myellipse[j], color, 2);
 minRects[j].points(pts);
 for (int k = 0; k < 4; k++) {
 line(dst, pts[k], pts[(k + 1)%4], color, 2);
 }
 }
 }
 imshow("output", dst);
 
}

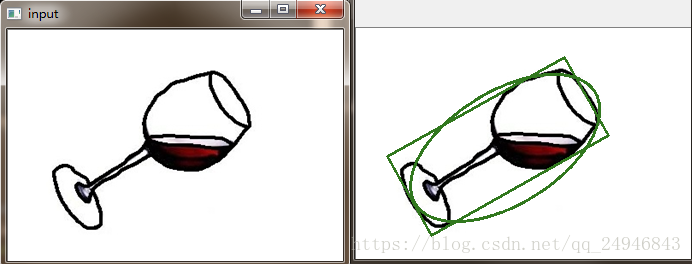
运行结果如下：

您可能感兴趣的文章:

加载全部内容