java红黑树的理解 通过java.util.TreeMap源码加强红黑树的理解

在此之前，已经为大家整理了很多关于经典问题红黑树的思路和解决办法。本篇文章，是通过分析java.util.TreeMap源码，让大家通过实例来对红黑树这个问题有更加深入的理解。

本篇将结合JDK1.6的TreeMap源码，来一起探索红-黑树的奥秘。红黑树是解决二叉搜索树的非平衡问题。

当插入（或者删除）一个新节点时，为了使树保持平衡，必须遵循一定的规则，这个规则就是红-黑规则： 
1) 每个节点不是红色的就是黑色的 
2) 根总是黑色的 
3) 如果节点是红色的，则它的子节点必须是黑色的（反之倒不一定必须为真） 
4) 从跟到叶节点或者空子节点的每条路径，必须包含相同数目的黑色节点

插入一个新节点

红-黑树的插入过程和普通的二叉搜索树基本一致：从跟朝插入点位置走，在每个节点处通过比较节点的关键字相对大小来决定向左走还是向右走。

public V put(K key, V value) {
Entry<K,V> t = root;
int cmp;
Entry<K,V> parent;
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0) {
t = t.left;
} else if (cmp > 0) {
t = t.right; 
} else {
// 注意，return退出方法 
return t.setValue(value); 
}
} while (t != null);
Entry<K,V> e = new Entry<K,V>(key, value, parent);
if (cmp < 0) {
parent.left = e;
} else {
parent.right = e;
}
fixAfterInsertion(e);
size++;
modCount++;
return null;
}

但是，在红-黑树种，找到插入点更复杂，因为有颜色变换和旋转。fixAfterInsertion()方法就是处理颜色变换和旋转，需重点掌握它是如何保持树的平衡(use rotations and the color rules to maintain the tree's balance)。

下面的讨论中，使用X、P、G表示关联的节点。X表示一个特殊的节点， P是X的父，G是P的父。

X is a node that has caused a rule violation. (Sometimes X refers to a newly inserted node, and sometimes to the child node when a parent and child have a redred conflict.)

On the way down the tree to find the insertion point, you perform a color flip whenever you find a black node with two red children (a violation of Rule 2). Sometimes the flip causes a red-red conflict (a violation of Rule 3). Call the red child X and the red parent P. The conflict can be fixed with a single rotation or a double rotation, depending on whether X is an outside or inside grandchild of G. Following color flips and rotations, you continue down to the insertion point and insert the new node.

After you've inserted the new node X, if P is black, you simply attach the new red node. If P is red, there are two possibilities: X can be an outside or inside grandchild of G. If X is an outside grandchild, you perform one rotation, and if it's an inside grandchild, you perform two. This restores the tree to a balanced state.

按照上面的解释，讨论可分为3个部分，按复杂程度排列，分别是: 
1) 在下行路途中的颜色变换（Color flips on the way down） 
2) 插入节点之后的旋转（Rotations after the node is inserted） 
3) 在向下路途上的旋转（Rotations on the way down）

在下行路途中的颜色变换（Color flips on the way down）

Here's the rule: Every time the insertion routine encounters a black node that has two red children, it must change the children to black and the parent to red (unless the parent is the root, which always remains black)

The flip leaves unchanged the number of black nodes on the path from the root on down through P to the leaf or null nodes.

尽管颜色变换不会违背规则4，但是可能会违背规则3。如果P的父是黑色的，则P由黑色变成红色时不会有任何问题，但是，如果P的父是红色的，那么在P的颜色变化之后，就有两个红色节点相连接了。这个问题需要在继续向下沿着路径插入新节点之前解决，可以通过旋转修正这个问题，下文将会看到。

插入节点之后的旋转（Rotations after the node is inserted）

新节点在插入之前，树是符合红-黑规则，在插入新节点之后，树就不平衡了，此时需要通过旋转来调整树的平衡，使之重新符合红-黑规则。

可能性1：P是黑色的，就什么事情也不用做。插入即可。

可能性2：P是红色，X是G的一个外侧子孙节点，则需要一次旋转和一些颜色的变化。 
以插入50,25,75,12,6为例，注意节点6是一个外侧子孙节点，它和它的父节点都是红色。 

在这个例子中，X是一个外侧子孙节点而且是左子节点，X是外侧子孙节点且为右子节点，是一种与此对称的情况。通过用50,25,75,87,93创建树，同理再画一画图，这里就省略了。

可能性3：P是红色，X是G的一个内侧子孙节点，则需要两次旋转和一些颜色的改变。 
以插入50,25,75,12,18为例，注意节点18是一个内侧子孙节点，它和它的父节点都是红色。 

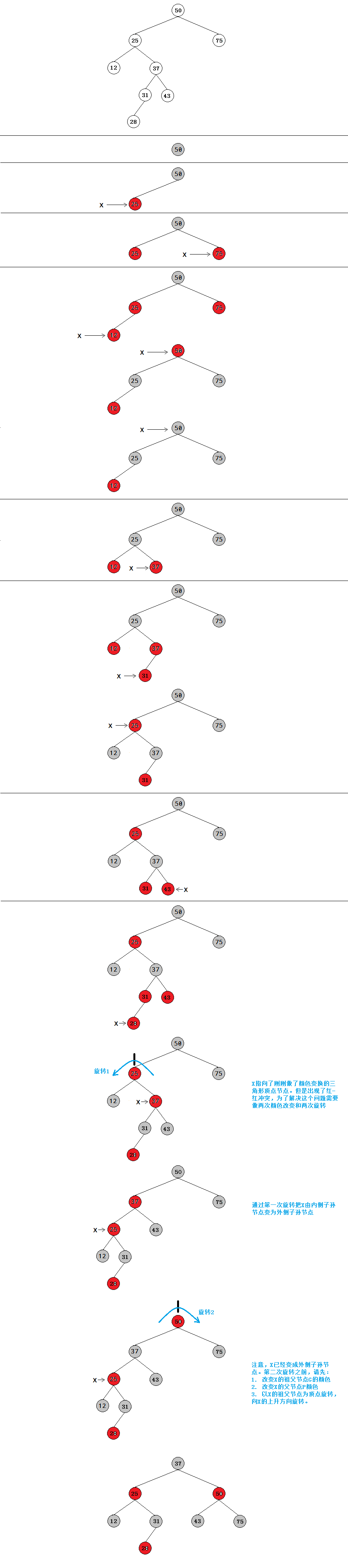
在向下路途上的旋转（Rotations on the way down）

在插入新节点之前，实际上树已经违背了红-黑规则，所以需要插入新节点之前做调整。所以我们本次讨论的主题是“在向下路途准备插入新节点时，上面先进行调整，使上面成为标准的红黑树后，再进行新节点插入”。

外侧子孙节点

以插入50,25,75,12,37,6,18,3为例，例子中违背规则的节点是一个外侧子孙节点。 

内侧子孙节点

以插入50,25,75,12,37,31,43为例，例子中违背规则的节点是一个内侧子孙节点。

红-黑树的效率

和一般的二叉搜索树类似，红-黑树的查找、插入和删除的时间复杂度为O(log2N)。

红-黑树的查找时间和普通的二叉搜索树的查找时间应该几乎完全一样。因为在查找过程中并没用到红-黑特征。额外的开销只是每个节点的存储空间都稍微增加了一点，来存储红黑颜色（一个boolean变量）。

final Entry<K, V> getEntry(Object key) {
Comparable <? super K > k = (Comparable <? super K > ) key;
Entry<K, V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0) {
p = p.left;
} else if (cmp > 0) {
p = p.right;
} else {
return p;
}
}
return null;
}

插入和删除的时间要增加一个常数因子，因为不得不在下行的路径上和插入点执行颜色变换和旋转。平均起来一次插入大约需要一次旋转。

因为在大多数应用中，查找的次数比插入和删除的次数多，所以应用红-黑树取代普通的二叉搜索树总体上不会增加太多的时间开销。