超级简单的二叉平衡排序树调整方法 — 看不懂你打我

相信很多学习数据结构的小伙伴们，在学习到 “二叉平衡数的调整方法 ” 时，教材上的方法看的云里雾里的，一看就会，一做就废......

什么 LL型、RR型、LR型、RL型的不平衡原因以及对应的调整方式，看得人快要疯了！

 

那么！现在，鄙人不才，自己总结出了一套超级简单的调整方法！！！

 

抛却复杂的课本知识，调整不需要分辨什么 LL、RR、LR、RL，只利用以下几步，轻松调整！

 

规定：

平衡二叉树均是左子树小于根节点，右子树大于根节点

在下方的示意图中：

1 米黄色圈表示教材上所说的最小不平衡子树

2 粉红的圈表示本文算法所提到的最小调整树

3 图中浅蓝色的数字代表每个结点此时的平衡因子

 

算法思路如下：

• 标平衡因子：先对所有的结点标记出平衡因子（平衡因子 = 该结点左子树深度 - 该结点右子树深度）

• 找最小调整树：

  • 最小不平衡子树（教材概念）：以插入路径上离插入结点最近的平衡因子的绝对值大于 1 的结点作为根的子树

  • 最小调整树（本文算法）：此处所说的最小调整树（本文算法规定只包含 3 个结点）与教材上有一点区别，需要分情况：

    • 情况一：最小不平衡子树中包含根节点时，最小调整树不包含刚插入的叶子节点

    • 情况二：最小不平衡子树中不包含根节点时，最小调整树包含刚插入的叶子结点

• 根据平衡因子调整结点位置

  • 结点命名规定：

    • 调整前：最小调整树永远只有 3 结点，并且一定处于不同的 3 层，从上到下依次命名为 A、B、C

    • 调整时：平衡因子最大的叫 Max，最小的叫 Min，大小处于两者中间的叫 temp；若两个结点的平衡因子刚好相等，则将最下面的 C 作为 temp，中间的 B 作为 Max

  • 调整原则：将结点 temp 及其所拥有的所有子树一起插入到 Min 和 Max 中间

  • 调整时针对 “找最小调整树” 步骤  中提到的两种情况，分别有不同的调整策略

    • 最小调整树 中 包含根节点 时

      • temp 结点带着它的子树一起向上移动，temp 结点插入到结点 Min 和 Max 中间

      • 当 temp 结点有左子树时，将 temp 的左子树连接在 Min 结点上

      • 当 temp 结点有右子树时，将 temp 的右子树连接在 Max 结点上

      • 最后，将 temp 结点作为新的根节点，捏住 temp 结点向上提，得到一棵新的树

      • 调整完毕

    • 最小调整树 中 不包含根节点 时

      • 将最小调整树从原树上断开，单独进行调整

      • 断开后，根据调整原则将 temp 结点插入到 Min 和 Max 的中间

      • 捏住结点 temp 向上提，形成新子树，将该新子树连接到原树中刚刚断开的地方

      • 调整完毕

 

什么？听不懂？感觉比教材还要云里雾里？没关系，一个例子搞定你的所有疑惑

【例】将关键字序列 {34，23，15，98，115，28，107} 插入到一颗空的平衡二叉排序树中，要求得到的树所有子树仍然满足平衡二叉排序树的性质

根据本算法进行的解题思路如下~~~

 

 

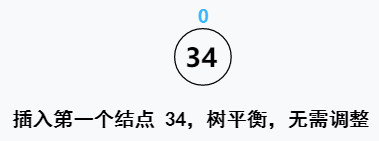
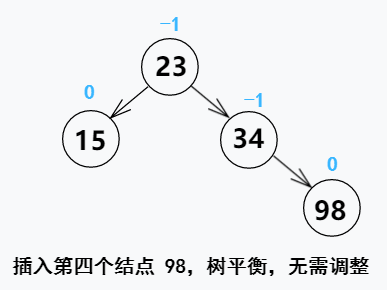
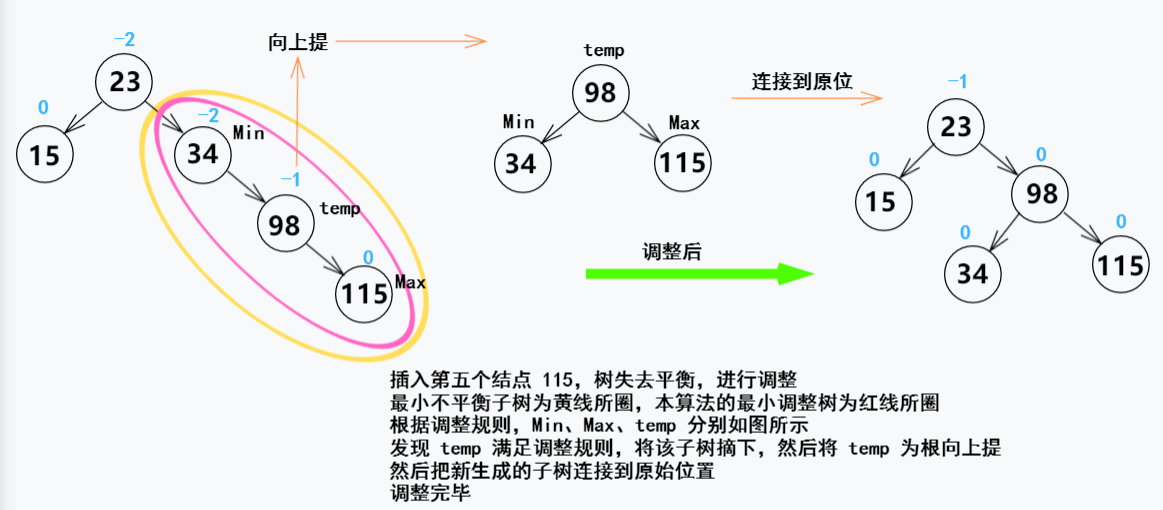
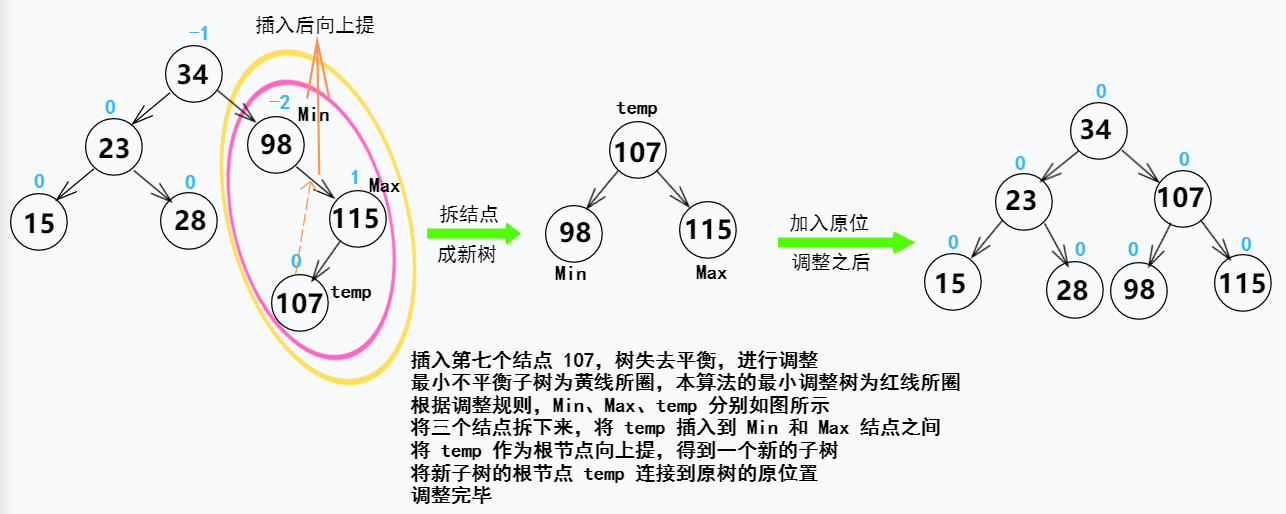
好啦！以上就是本算法的所有思路及例子了，是不是比教材上什么单左旋、单右旋、先左旋后右旋、先右旋后左旋来的简单多了~~~