代码仓库: https://github.com/brandonlyg/cute-dl

目标

1. 增加交叉熵损失函数，使框架能够支持分类任务的模型。
2. 构建一个MLP模型, 在mnist数据集上执行分类任务准确率达到91%。
   
   

实现交叉熵损失函数

数学原理

分解交叉熵损失函数

        交叉熵损失函数把模型的输出值当成一个离散随机变量的分布列。 设模型的输出为: \(\hat{Y} = f(X)\), 其中\(f(X)\)表示模型。\(\hat{Y}\)是一个m X n矩阵, 如下所示:

        把这个矩阵的第i行记为\(\hat{y}_i\), 它是一个\(\\R^{1Xn}\)向量, 它的第j个元素记为\(\hat{y}_{ij}\)。
        交叉熵损失函数要求\(\hat{y}_i\)具有如下性质:

        特别地，当n=1时, 只需要满足第一条性质即可。我们先考虑n > 1的情况, 这种情况下n=2等价于n=1，在工程上n=1可以看成是对n=2的优化。
        模型有时候并不会保证输出值有这些性质, 这时损失函数要把\(\hat{y}_i\)转换成一个分布列:\(\hat{p}_i\), 转换函数的定义如下:

        这里的\(\hat{p}_i\)是可以满足要求的。函数\(e^{\hat{y}_{ij}}\)是单调增函数，对于任意两个不同的\(\hat{y}_{ia} ＜ \hat{y}_{ib}\), 都有:\(e^{\hat{y}_{ia}}\) ＜ \(e^{\hat{y}_{ib}}\), 从而得到:\(\hat{p}_{ia} ＜ \hat{p}_{ib}\). 因此这个函数把模型的输出值变成了概率值，且概率的大小关系和输出值的大小关系一致。
        设数据\(x_i\)的类别标签为\(y_i\)∈\(\\R^{1Xn}\). 如果\(x_i\)的真实类别为t, \(y_i\)满足:

        \(y_i\)使用的是one-hot编码。交叉熵损失函数的定义为:

        对于任意的\(y_{ij}\), 损失函数中任意一项具有如下的性质:

        可看出\(y_{ij}=0\)的项对损失函数的值不会产生影响，所以在计算时可以把这样的项从损失函数中忽略掉。其它\(y_{ij}=1\)的项当\(\hat{p}_{ij}=y_{ij}=1\)时损失函数达到最小值0。

梯度推导

        根据链式法则, 损失函数的梯度为:

        其中:

        把(2), (3)代入(1)中得到:

        由于当\(y_{ij}=0\)时, 梯度值为0, 所以这种情况可以忽略, 最终得到的梯度为:

        如果模型的输出值是一个随机变量的分布列, 损失函数就可以省略掉把\(\hat{y}_{ij}\)转换成\(\hat{p}_{ij}\)的步骤, 这个时候\(\hat{y}_{ij} = \hat{p}_{ij}\), 最终的梯度变成:

交叉熵损失函数的特殊情况: 只有两个类别

        现在来讨论当n=1的情况, 这个时候\(\hat{y}_i\) ∈ \(\\R^{1 X 1}\)，可以当成标量看待。
        如果模型输出的不是分布列, 损失函数可以分解为:

        损失函数关于输出值的梯度为:

        把(1),(2)代入(3)中得到:

        如果模型输出值时一个随机变量的分布列, 则有:

实现代码

        这个两种交叉熵损失函数的实现代码在cutedl/losses.py中。一般的交叉熵损失函数类名为CategoricalCrossentropy, 其主要实现代码如下:

  '''
  输入形状为(m, n)
  '''
  def __call__(self, y_true, y_pred):
      m = y_true.shape[0]
      #pdb.set_trace()
      if not self.__form_logists:
          #计算误差
          loss = (-y_true*np.log(y_pred)).sum(axis=0)/m
          #计算梯度
          self.__grad = -y_true/(m*y_pred)
          return loss.sum()

      m = y_true.shape[0]
      #转换成概率分布
      y_prob = dlmath.prob_distribution(y_pred)
      #pdb.set_trace()
      #计算误差
      loss = (-y_true*np.log(y_prob)).sum(axis=0)/m
      #计算梯度
      self.__grad  = (y_prob - y_true)/m

      return loss.sum()

        其中prob_distribution函数把模型输出转换成分布列, 实现方法如下:

def prob_distribution(x):
    expval = np.exp(x)
    sum = expval.sum(axis=1).reshape(-1,1) + 1e-8

    prob_d = expval/sum

    return prob_d

        二元分类交叉熵损失函数类名为BinaryCrossentropy, 其主要实现代码如下:

'''
输入形状为(m, 1)
'''
def __call__(self, y_true, y_pred):
    #pdb.set_trace()
    m = y_true.shape[0]

    if not self.__form_logists:
        #计算误差
        loss = (-y_true*np.log(y_pred)-(1-y_true)*np.log(1-y_pred))/m
        #计算梯度
        self.__grad = (y_pred - y_true)/(m*y_pred*(1-y_pred))
        return loss.sum()

    #转换成概率
    y_prob = dlmath.sigmoid(y_pred)
    #计算误差
    loss = (-y_true*np.log(y_prob) - (1-y_true)*np.log(1-y_prob))/m
    #计算梯度
    self.__grad = (y_prob - y_true)/m

    return loss.sum()

在MNIST数据集上验证

        现在使用MNIST分类任务验证交叉熵损失函数。代码位于examples/mlp/mnist-recognize.py文件中. 运行这个代码前先把原始的MNIST数据集下载到exampleshttps://img.qb5200.com/download-x/datasets/下并解压. 数据集下载链接为：http://pan.baidu.com/s/1CmYYLyLJ87M8wH2iQWrrFA，密码: 1rgr

        训练模型的代码如下:

'''
训练模型
'''
def fit():
    inshape = ds_train.data.shape[1]
    model = Model([
                nn.Dense(10, inshape=inshape, activation='relu')
            ])
    model.assemble()

    sess = Session(model,
            loss=losses.CategoricalCrossentropy(),
            optimizer=optimizers.Fixed(0.001)
            )

    stop_fit = session.condition_callback(lambda :sess.stop_fit(), 'val_loss', 10)

    #pdb.set_trace()
    history = sess.fit(ds_train, 20000, val_epochs=5, val_data=ds_test,
                        listeners=[
                            stop_fit,
                            session.FitListener('val_end', callback=accuracy)
                        ]
                    )

    fit_report(history, report_path+"0.png")

        拟合报告:

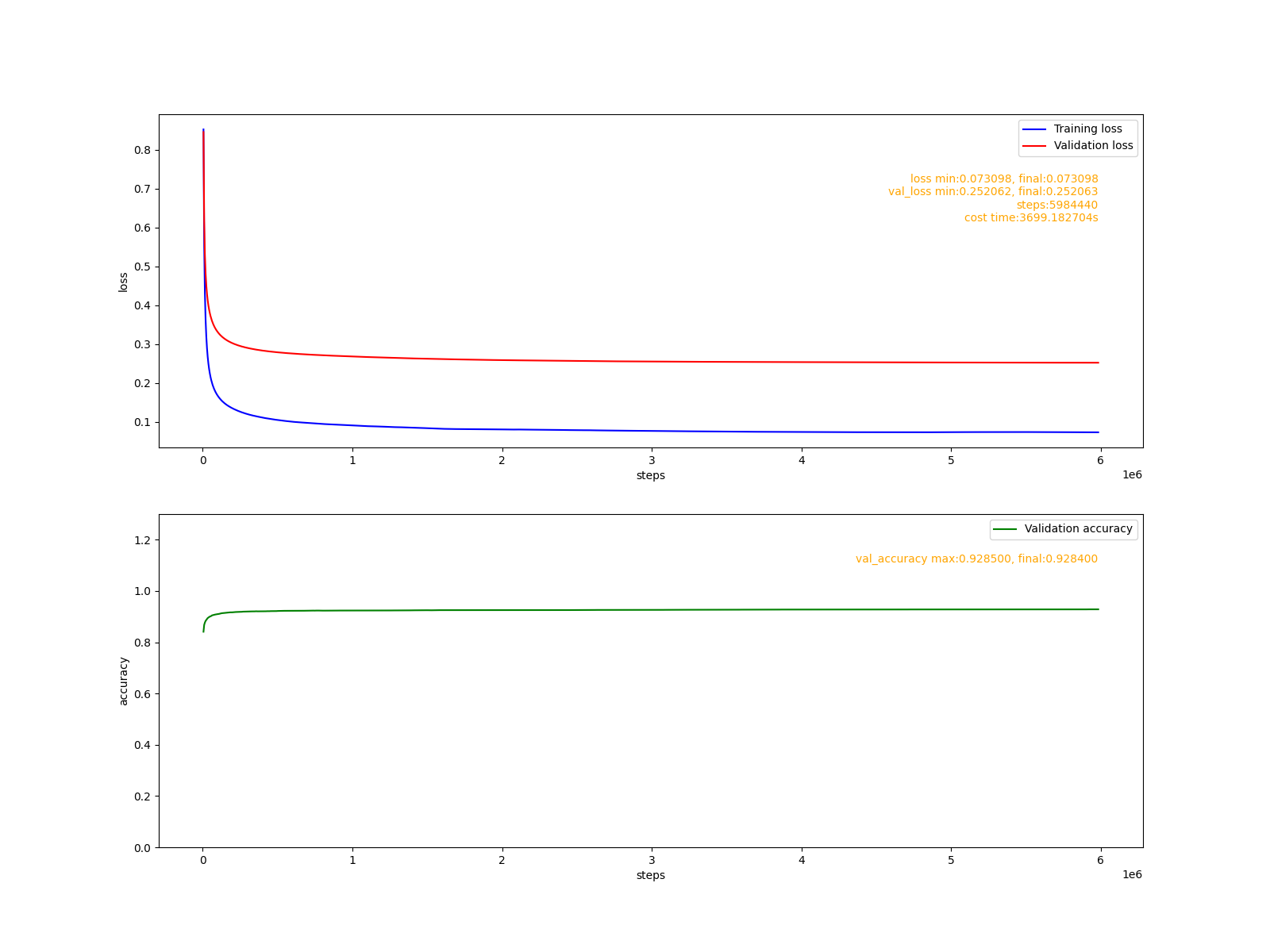
        可以看出，通过一个小时(3699s), 将近600万步的训练，模型准确率达到了92%。同样的模型在tensorflow(CPU版)中经过十几分钟的训练即可达到91%。这说明, cute-dl框架在任务性能上是没问题的，但训练模型的速度欠佳。

总结

        这个阶段框架实现了对分类任务的支持, 在MNIST数据集上验证模型性能达到预期。模型训练的速度并不令人满意。
        下个阶段，将会给模型添加学习率优化器, 在不损失泛化能力的同时加快模型训练速度。