python K-means轨迹聚类 python 基于空间相似度的K-means轨迹聚类的实现
weixin_41669147 人气:1想了解python 基于空间相似度的K-means轨迹聚类的实现的相关内容吗，weixin_41669147在本文为您仔细讲解python K-means轨迹聚类的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：python,K-means轨迹聚类,python,K-means,聚类,python,轨迹聚类，下面大家一起来学习吧。
这里分享一些轨迹聚类的基本方法，涉及轨迹距离的定义、kmeans聚类应用。
需要使用的python库如下
import pandas as pd import numpy as np import random import os import matplotlib.pyplot as plt import seaborn as sns from scipy.spatial.distance import cdist from itertools import combinations from joblib import Parallel, delayed from tqdm import tqdm
数据读取
假设数据是每一条轨迹一个excel文件，包括经纬度、速度、方向的航班数据。我们从文件中读取该数据，保存在字典中。
获取数据的地址，假设在多个文件中
def get_alldata_path(path):
all_path = pd.DataFrame(columns=['path_root','path0','path1','path2','path','datalist'])
path0 = os.listdir(path)
for path_temp0 in path0:
path1 = os.listdir(path+path_temp0)
for path_temp1 in path1:
path2 = os.listdir(path+path_temp0+'\\'+path_temp1)
for path_temp2 in path2:
path3 = os.listdir(path+path_temp0+'\\'+path_temp1+'\\'+path_temp2)
all_path.loc[all_path.shape[0]] = [path,path_temp0,path_temp1,path_temp2,
path+path_temp0+'\\'+path_temp1+'\\'+path_temp2+'\\',
path3]
return all_path
这样你就可以得到你的数据的地址，方便后面读取需要的数据
#设置数据根目录 path = 'yourpath' #获取所有数据地址 data_path = get_alldata_path(path)
读取数据，保存成字典格式，字典的key是这条轨迹的名称，value值是一个DataFrame，需要包含经纬度信息。
def read_data(data_path,idxs):
'''
功能：读取数据
'''
data = {}
for idx in idxs:
path_idx = data_path['path'][idx]
for dataname in data_path['datalist'][idx]:
temp = pd.read_excel(path_idx+dataname,header=None)
temp = temp.loc[:,[4,5,6,8]]
temp.replace('none',np.nan,inplace=True)
temp.replace('Trak',np.nan,inplace=True)
temp = temp.dropna().astype(float)
temp.columns = ['GPSLongitude','GPSLatitude','direction','speed']
data[str(idx)+'_'+dataname] = temp
return data
读取你想要的数据，前面读取到的地址也是一个DataFrame，选择你想要进行聚类的数据读取进来。
#读取你想要的数据 idxs = [0,1,2] data = read_data(data_path,idxs)
定义不同轨迹间的距离
这里使用了双向的Hausdorff距离（双向豪斯多夫距离）
给定两条轨迹A和B,其中轨迹A上有n个点,轨迹B上有m个点。它们之间的空间相似距离d定义为:
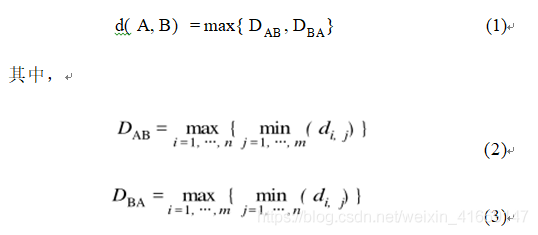
其中，di ,j 是一条轨迹上的第 i个点到另一条轨迹上的 第 j 个 点之间的多因素欧氏距离。可见, 如果轨迹 A 和 B 越相似, 它们之间的距离就越小, 反之则越大。
def OneWayHausdorffDistance(ptSetA, ptSetB):
# 计算任意向量之间的距离，假设ptSetA有n个向量，ptSetB有m个向量
# 得到矩阵C（n行m列）Cij代表A中都第i个向量到B中第j向量都距离
dist = cdist(ptSetA, ptSetB, metric='euclidean')
# np.min(dist,axis=1):计算每一行的的最小值
# 即：固定点集A的值，求点集A中到集合B的最小值
return np.max(np.min(dist, axis=1))
# 计算双向的Hausdorff距离=====>H(ptSetA,ptSetB)=max(h(ptSetA,ptSetB),h(ptSetB,ptSetA))
# ptSetA：输入的第一个点集
# ptSetB：输入的第二个点集
# Hausdorff距离度量了两个点集间的最大不匹配程度
def HausdorffDistance(ptSetA, ptSetB):
# 计算双向的Hausdorff距离距离
res = np.array([
OneWayHausdorffDistance(ptSetA, ptSetB),
OneWayHausdorffDistance(ptSetB, ptSetA)
])
return np.max(res)
计算距离矩阵
每个轨迹数据都包含经纬度、速度、方向，分别计算距离，然后根据一定的比例相加，活动最终的距离。
def DistanceMat(data,w=[0.7,0.2,0.1]):
'''
功能：计算轨迹段的距离矩阵
输出：距离矩阵
'''
#要计算的组合
ptCom = list(combinations(list(data.keys()),2))
#基于轨迹的距离
distance_tra = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)(
data[ptSet1][['GPSLongitude','GPSLatitude']],data[ptSet2][['GPSLongitude','GPSLatitude']]
) for ptSet1,ptSet2 in ptCom)
distancemat_tra = pd.DataFrame(ptCom)
distancemat_tra['distance'] = distance_tra
distancemat_tra = distancemat_tra.pivot(index=0,columns=1,values='distance')
for pt1 in data.keys():
distancemat_tra.loc[str(pt1),str(pt1)] = 0
distancemat_tra = distancemat_tra.fillna(0)
distancemat_tra = distancemat_tra.loc[list(data.keys()),list(data.keys())]
distancemat_tra = distancemat_tra+distancemat_tra.T
#基于方向的距离
distance_speed = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)(
data[ptSet1][['speed']],data[ptSet2][['speed']]
) for ptSet1,ptSet2 in ptCom)
distancemat_speed = pd.DataFrame(ptCom)
distancemat_speed['distance'] = distance_speed
distancemat_speed = distancemat_speed.pivot(index=0,columns=1,values='distance')
for pt1 in data.keys():
distancemat_speed.loc[str(pt1),str(pt1)] = 0
distancemat_speed = distancemat_speed.fillna(0)
distancemat_speed = distancemat_speed.loc[list(data.keys()),list(data.keys())]
distancemat_speed = distancemat_speed+distancemat_speed.T
#基于方向的距离
distance_direction = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)(
data[ptSet1][['direction']],data[ptSet2][['direction']]
) for ptSet1,ptSet2 in ptCom)
distancemat_direction = pd.DataFrame(ptCom)
distancemat_direction['distance'] = distance_direction
distancemat_direction = distancemat_direction.pivot(index=0,columns=1,values='distance')
for pt1 in data.keys():
distancemat_direction.loc[str(pt1),str(pt1)] = 0
distancemat_direction = distancemat_direction.fillna(0)
distancemat_direction = distancemat_direction.loc[list(data.keys()),list(data.keys())]
distancemat_direction = distancemat_direction+distancemat_direction.T
distancemat_tra = (distancemat_tra-distancemat_tra.min().min())/(distancemat_tra.max().max()-distancemat_tra.min().min())
distancemat_speed = (distancemat_speed-distancemat_speed.min().min())/(distancemat_speed.max().max()-distancemat_speed.min().min())
distancemat_direction = (distancemat_direction-distancemat_direction.min().min())/(distancemat_direction.max().max()-distancemat_direction.min().min())
distancemat = w[0]*distancemat_tra+w[1]*distancemat_speed+w[2]*distancemat_direction
return distancemat
使用前面读取的数据，计算不同轨迹间的距离矩阵，缺点在于计算时间会随着轨迹数的增大而指数增长。
distancemat = DistanceMat(data,w=[0.7,0.2,0.1])
k-means聚类
获得了不同轨迹间的距离矩阵后，就可以进行聚类了。这里选择k-means，为了得到更好的结果，聚类前的聚类中心选取也经过了一些设计，排除了随机选择，而是选择尽可能远的轨迹点作为 初始中心。
初始化聚类“中心”。随机选取一条轨迹作为第一类的中心, 即选取一个轨迹序列作为聚类的初始“中心。然后在剩下的 L - 1 个序列中选取一个序列 X 2 作为第二类的中心 C 2 , 设定一个阈值 q, 使其到第一类的中心 C 1 的距离大于q。
class KMeans:
def __init__(self,n_clusters=5,Q=74018,max_iter=150):
self.n_clusters = n_clusters #聚类数
self.Q = Q
self.max_iter = max_iter # 最大迭代数
def fit(self,distancemat):
#选择初始中心
best_c = random.sample(distancemat.columns.tolist(),1)
for i in range(self.n_clusters-1):
best_c += random.sample(distancemat.loc[(distancemat[best_c[-1]]>self.Q)&(~distancemat.index.isin(best_c))].index.tolist(),1)
center_init = distancemat[best_c] #选择最小的样本组合为初始质心
self._init_center = center_init
#迭代停止条件
iter_ = 0
run = True
#开始迭代
while (iter_<self.max_iter)&(run==True):
#聚类聚类标签更新
labels_ = np.argmin(center_init.values,axis=1)
#聚类中心更新
best_c_ = [distancemat.iloc[labels_== i,labels_==i].sum().idxmin() for i in range(self.n_clusters)]
center_init_ = distancemat[best_c_]
#停止条件
iter_ += 1
if best_c_ == best_c:
run = False
center_init = center_init_.copy()
best_c = best_c_.copy()
#记录数据
self.labels_ = np.argmin(center_init.values,axis=1)
self.center_tra = center_init.columns.values
self.num_iter = iter_
self.sse = sum([sum(center_init.iloc[self.labels_==i,i]) for i in range(self.n_clusters)])
应用聚类，根据平方误差和SSE结合手肘法确定最佳的聚类数，使用最佳的聚类数获得最后聚类模型。
#聚类，保存不同的sse
SSE = []
for i in range(2,30):
kmeans = KMeans(n_clusters=i,Q=0.01,max_iter=150)
kmeans.fit(distancemat)
SSE.append(kmeans.sse)
#画图
plt.figure(0)
plt.plot(SSE)
plt.show()
#使用最好的结果进行聚类
n_clusters=12
kmeans = KMeans(n_clusters=n_clusters,Q=0.01,max_iter=150)
kmeans.fit(distancemat)
kmeans.sse #输出sse
kmeans.labels_ #输出标签
kmeans.center_tra #输出聚类中心
#画图，不同类的轨迹使用不同的颜色
plt.figure(1)
for i in range(n_clusters):
for name in distancemat.columns[kmeans.labels_==i]:
plt.plot(data[name].loc[:,'GPSLongitude'],data[name].loc[:,'GPSLatitude'],c=sns.xkcd_rgb[list(sns.xkcd_rgb.keys())[i]])
plt.show()
#保存每一个轨迹属于哪一类
kmeans_result = pd.DataFrame(columns=['label','id'])
for i in range(n_clusters):
kmeans_result.loc[i] = [i,distancemat.columns[kmeans.labels_==i].tolist()]
加载全部内容