【图机器学习】cs224w Lecture 7 - 节点的表示

转自本人：https://blog.csdn.net/New2World/articlehttps://img.qb5200.com/download-x/details/105536633

Node Embedding

上一讲介绍了对图中节点进行分类的方法，涉及了节点自身的特征以及图的结构信息。然而当特征这个概念出现就说明需要做特征工程，这是相当费时费力的工作。最后的结果还不一定理想，因为或多或少会丢失一些信息。因此我们希望能让算法自己学习节点特征，虽然这样的到的特征向量并不像传统意义上的特征那样每一列有明确的意义，而更有一种对节点进行编码(embedding)的味道。其中最简单的例子就是 one-hot，但这种简单 embedding 的方式存在很多问题，比如泛化性差，维度高，信息缺失等。因此我们希望得到的 embedding 有一些很好的性质，比如 embedding 的相似度能反映节点在网络中的相似度。这里的相似度是根据不同应用场景进行定义的，可以是拓扑结构上的相邻，也可以是之前提到的相同的角色。embedding 的相似度计算也需要针对不用应用场景或需求来定义，但一般情况下采用的还是向量的内积。
有了这个大体思路我们就可以将这个学习节点 embedding 的过程简单分为 3 步：

1. 定义一个编码器
2. 定义节点的相似度
3. 对编码器的参数进行优化，使得 \(similarity(u,v)\approx z_v^Tz_u\)

Random Walk

随机游走，正如这个名字描述的那样，节点从一个点开始沿着图中的边“乱”跑，途经的节点的 multiset(节点可重复) 就是我们想要的东西。为什么我们要这种看似无章可循的“乱”生成的结果？这其实是定义节点相似度的一种方法。假设现在我们需要节点 \(u\) 的 embedding，且我们希望节点相似度定义为结构上较为接近的点具有更高相似度。那最容易想到的方法就是邻接节点，这些点的相似度一定很高，这要能最大化这一部分点的 embedding 相似度就好了。想法很好也很正确，但是这样做存在两个问题。首先，如果只找邻接节点，那获得的信息就只有 \(1\) hop，这样得到的结果太局限了。再说直观上也说不通，就好比和节点 \(u\) 直接相连的节点和 \(u\) 很类似，而 \(u\) 邻接点的邻接点就和 \(u\) 完全没有关系了。那可能就有人说，大不了我多迭代几次，考虑跑个 \(k\) hop。那么这就涉及到第二个问题，对于大规模的网络一部分节点的度很高，例如微软 MSN 的网络最高的度是指数级别的，因此找所有邻接节点代价太高更别说还要找邻接点的邻接点了。
这么一来，这个随机游走看起来是不是就很漂亮了。首先它随机传播，只要我们控制好传播距离就能实现多 hop。其次它不要求遍历所有邻接点，但只要随机次数足够它还是能覆盖大部分邻接点。
然后根据随机游走的结果来定义相似度就很简单了，即节点 \(u\) 和 \(v\) 的 embedding 相似度和这两个节点同时出现在随机游走的结果中的概率成正比。你细品是不是这个道理。
有了相似度，接下来就是优化的过程。我们用 log-likelihood 来做。这里将随机游走的结果记为 \(N_R(u)\)

然后因为是概率，所以我们用 softmax 来定义 \(P(v|z_u)\)

为什么是 softmax ？
因为 \(\sum_i\exp(x_i)\approx\max_i\exp(x_i)\)

然而就算 numpy 再方便再快也经不起套娃的 sum 那 \(O(|V|^2)\) 的复杂度呀。于是采用了 negative sampling 的方法取代每次计算所有节点相似度和的步骤。negative sampling 说白了就是从所有节点中按照分布 \(P_V\) 随机选点。在这个场景下，每个点被选中的概率和它自身的 degree 成正比。

随机选一些点不是会损失很多精度吗？看起来是的，但实际上这样做没什么问题。为什么？这个过程很复杂，有空我再去看，paper 链接先放这儿 https://arxiv.org/pdf/1402.3722.pdf
这里的 \(k\) 是 negative sampling 选点的超参数，一般来说 \(k\) 取 \(5\)~\(20\)。太高的 \(k\) 虽然能得到更稳定的结果，但 bias 会增加，因为选点概率和度成正比。

node2vec

上面提到的这种是长度固定的无偏随机游走。它的约束太强了导致得到的 embedding 泛化能力有限。这也是一个很重要的点，即更宽松的约束条件下得到的 embedding 更丰富。接下来介绍的这个也是随机游走，但它的规则不一样。slide 里介绍的这是一个有偏的二阶随机游走，有偏会在下面介绍，但这里我是没看出来哪里体现了二阶。
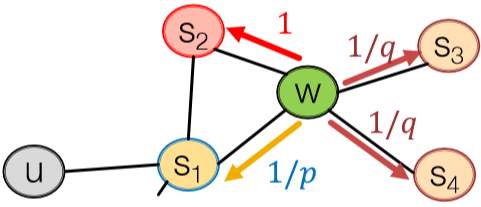
node2vec 里有两个关键超参数，return \(p\) 和 in-out \(q\)。下图很直观地展示了这两个参数的用途。首先从 \(s_1\) 出发到达 \(w\) 后需要决定下一步走哪里，我们按 \(1/p\) 的相对概率回到 \(s_1\)，\(1\) 的相对概率进行 BFS 即 \(s_1\) 的下一个邻接节点，或者按 \(1/q\) 的相对概率传播出去即 DFS。如此一来就能 capture 到局部和全局特征了。这种方法在节点分类任务里效果很好。
注意，这里并不是概率，而是相对概率关系。

接下来就是用 SGD 做优化了。

TransE

TransE 其实也是一个学习节点 embedding 的算法。我对这个算法比较感兴趣，因为我一直想涉足知识图谱领域，而且我本科导师带的研究生就在做 TransE 相关的东西，我也或多或少了解过一点它的神奇特性。比如现在我们的图谱里有几个实体：“北京”，“中国”，“华盛顿”，“美国”；同时还有关系：“中国”\(\rightarrow\)“北京”，“美国”\(\rightarrow\)“华盛顿”。显而易见这个关系其实是“首都”的含义，那么 TransE 能做到 “中国” - “北京” = “美国” - “华盛顿” = “首都” (当然，其实并没有“首都”这么一个实体，只是方便解释)。而这一特性就能完成 link prediction 的任务。比如我现在有“巴黎”和“法国”但没有这两个实体见的关系，那我们可以做的就是计算出 “法国” - “首都” 然后计算得到的结果和其它城市实体的相似度，而最终会发现“巴黎”的相似度最高。
之所以 TransE 能做到这一点，跟它的计算方式有关。它并非采用的随机游走的方法，而是采用上面说到的这种特性来做的优化。首先将实体和关系定义为三元组 \((h,l,t)\)，分别表示头实体、关系和尾实体 (有向)。然后

由此可见，随机游走并不是生成节点 embedding 的唯一方法，条条大路通罗马。

Embedding Entire Graph

最后一部分对整个图做 embedding 讲得很匆忙，我之前也没有太多关心过这个问题。不过根据 slide 自己理解了下。大致有三种方法

1. 暴力求和
2. 虚拟点表示图或子图，然后用标准的 embedding 方法来做。参考 Li et al., 2016
3. Anonymous walk

Anonymous Walk

这个玩意儿很神奇。它的定义和国内小学语文题类似，比如写出形如 AABB 的词语。但是这样的话有个疑惑，图中的 ABCDE 是怎么标的？事先有标签？还是怎么做？不是无监督学习吗？这需要看看论文再回来解决。

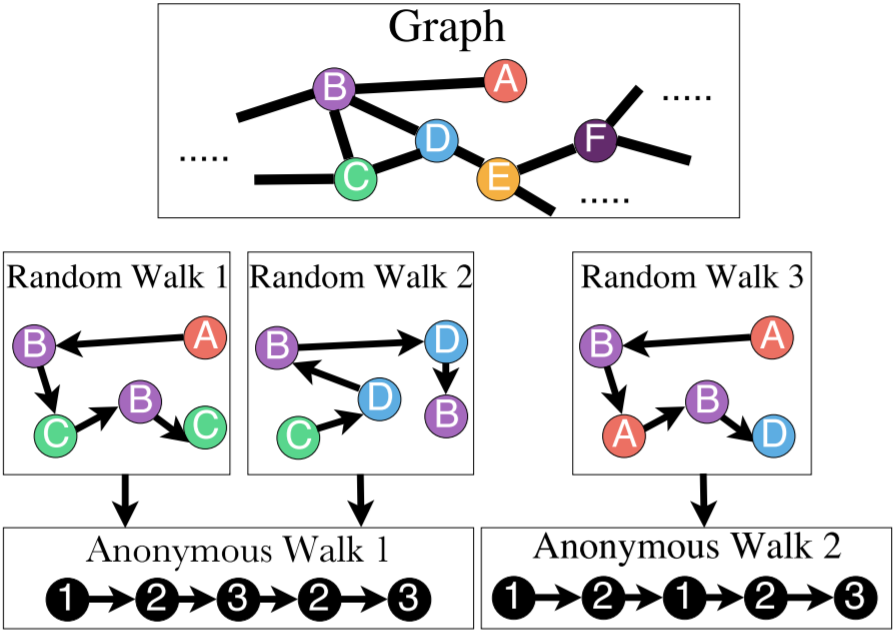
利用 anon. walk 也有几种方法来 embed 整个图。

第一种方法，我们先枚举出长度为 \(l\) 的所有 anon. walk，然后将图的 embedding 表示为这些游走的概率分布。比如长度为 \(3\) 的话就有 \(5\) 中排列，那么图的 embedding 就是一个 5D 向量。

第二种方法，我们生成 \(m\) 个随机游走的结果，然后根据这个结果计算经验分布。而这个 \(m\) 的取值是有下界的，我们希望误差大于 \(\varepsilon\) 的概率小于 \(\delta\) 的话

其中 \(\eta\) 是长度为 \(l\) 的 anon. walk 的个数。

第三种方法，既然是机器学习那何不连游走过程一起学了？这里的 idea 是希望能编码游走过程使得下一个游走能被预测，即 \(P(w_t^u|w_{t-\Delta}^u,...,w_{t-1}^u)\) 这里的 \(w_t^u\) 是从节点 \(u\) 出发的第 \(t\) 个随机游走。

1. 从节点 \(u\) 开始跑 \(T\) 次 Rnd walk 得到 \(N_R(u)=\{w_1^u,w_2^u,...,w_T^u\}\)
2. 然后给定长度为 \(Delta\) 的滑窗，让算法学着预测在滑窗内同时出现的 walk

这里 \(b\in\R\)，\(U\in\R^D\)，\(z_i\) 是 anon. walk 的 embedding。详细参考 Anonymous Walk Embeddings, ICML 2018

Reference

[1]: 这儿有一篇关于各种 embedding 方法的 survey：Goyal and Ferrara, 2017