概述
在图形学渲染管线中,一个顶点坐标,大概要经历局部坐标系、世界坐标系、相机坐标系、裁剪坐标系,最后到窗口坐标系,显示在屏幕上。

在这些过程中,从一个坐标系到另一个坐标系,都需要进行一定的变换。下面,将介绍每次变换的方式。
注意,本文是针对OpenGL的。
局部空间->世界空间
这一变换过程,主要是将模型放置在世界空间中,进行一定的缩放、旋转或平移。这一步比较简单,只要将相应的矩阵作用到模型的局部空间坐标即可。
比如,对模型缩放\(\left(S_{x},S_{y},S_{z} \right)\),然后绕Z轴旋转\(\theta\)度,再进行\(\left(T_{x},T_{y},T_{z} \right)\)的平移。注意,这里的变换顺序是不能变的,即要先进行缩放,再进行旋转,最后进行平移。据此,我们可以构建模型变换矩阵。
\[M_{model}=
\begin{bmatrix}
1 & 0 & 0 & T_{x} \\
0 & 1 & 0 & T_{y} \\
0 & 0 & 1 & T_{z} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
\cos{\theta} & -\sin{\theta} & 0 & 0 \\
\sin{\theta} & \cos{\theta} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
S_{x} & 0 & 0 & 0 \\
0 & S_{y} & 0 & 0 \\
0 & 0 & S_{z} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
世界空间->相机空间
首先定义一下相机:
-
坐标为\(\vec{e}\)
-
观察方向\(\vec{g}\)
-
向上方向\(\vec{t}\)
示意图如下所示:

有一个性质注意一下:当相机和相机“看“到的物体一起变换时,相机”看“到的内容是不变的。这样,可以将相机的坐标移动到世界坐标的原点,向上方向对齐世界坐标的Y轴,观察方向对齐世界坐标的-Z轴。然后,对物体进行相同的变换即可。
在数学上,这个过程大概这样:
- 将相机移动到坐标原点
- 旋转观察方向\(\vec{g}\)到-Z轴
- 旋转向上方向\(\vec{t}\)到Y轴
- 旋转(\(\vec{g} \times \vec{t}\))到X轴
大体分为两步:先位移,后旋转。即\(M_{view} = R_{view}T_{view}\)。
平移部分:
\[T_{view} =
\begin{bmatrix}
1 & 0 & 0 & -x_{e} \\
0 & 1 & 0 & -y_{e} \\
0 & 0 & 1 & -z_{e} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
对于旋转部分,先补充一些知识点。对于二维空间来说:
\[R_{\theta} =
\begin{pmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta} \\
\end{pmatrix}
\]
\[R_{-\theta} =
\begin{pmatrix}
\cos{\theta} & \sin{\theta} \\
-\sin{\theta} & \cos{\theta} \\
\end{pmatrix} =
R_{\theta}^\mathrm{T}
\]
根据定义,旋转\(\theta\)角度和旋转\(-\theta\)角度是互逆的,即:\(R_{-\theta} = R_{\theta}^{-1}\)。
所以,对于旋转变换,可以得出旋转矩阵的逆等于它的转置,即:
\[R_{\theta}^\mathrm{T} = R_{\theta}^{-1}
\]
回到上面的旋转部分,直接求相机的坐标轴旋转到世界坐标轴的矩阵不是很方便,但是反过来,求世界坐标轴旋转到相机的坐标轴很容易:
\[R_{view}^{-1} =
\begin{bmatrix}
x_{\vec{g} \times \vec{t}} & x_{\vec{t}} & x_{-\vec{g}} & 0 \\
y_{\vec{g} \times \vec{t}} & y_{\vec{t}} & y_{-\vec{g}} & 0 \\
z_{\vec{g} \times \vec{t}} & z_{\vec{t}} & z_{-\vec{g}} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
根据旋转矩阵的逆等于它的转置,得出:
\[R_{view} =
(R_{view}^{-1})^\mathrm{T} =
\begin{bmatrix}
x_{\vec{g} \times \vec{t}} & y_{\vec{g} \times \vec{t}} & z_{\vec{g} \times \vec{t}} & 0 \\
x_{\vec{t}} & y_{\vec{t}} & z_{\vec{t}} & 0 \\
x_{-\vec{g}} & y_{-\vec{g}} & z_{-\vec{g}} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
根据\(M_{view} = R_{view}T_{view}\),可以得出:
\[M_{view} =
R_{view}T_{view} =
\begin{bmatrix}
x_{\vec{g} \times \vec{t}} & y_{\vec{g} \times \vec{t}} & z_{\vec{g} \times \vec{t}} & 0 \\
x_{\vec{t}} & y_{\vec{t}} & z_{\vec{t}} & 0 \\
x_{-\vec{g}} & y_{-\vec{g}} & z_{-\vec{g}} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -x_{e} \\
0 & 1 & 0 & -y_{e} \\
0 & 0 & 1 & -z_{e} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
相机空间->裁剪空间
在一个顶点着色器运行的最后,期望所有的坐标都能落在一个特定的范围内,且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略,所以剩下的坐标就将变为屏幕上可见的片段。这也就是裁剪空间(Clip Space)名字的由来。
因为将所有可见的坐标都指定在-1.0到1.0的范围内不是很直观,所以我们会指定自己的坐标集(Coordinate Set)并将它变换回标准化设备坐标系。
由投影矩阵创建的观察箱(Viewing Box)被称为平截头体(Frustum),每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将特定范围内的坐标转化到标准化设备坐标系的过程(而且它很容易被映射到2D观察空间坐标)被称之为投影(Projection),因为使用投影矩阵能将3D坐标投影(Project)到很容易映射到2D的标准化设备坐标系中。
这里要注意一下,OpenGL是右手坐标系的,但是在NDC中,是左手坐标系的,这里要特别注意!!!
相机空间转换到裁剪空间,有需要用到投影变换。有两种投影变换:正交投影和透视投影。下面分别介绍一下。
正交投影
我们先定义一个正交投影的视锥体\([l,r] \times [b,t] \times [f,n]\)(注意,n和f都是负数,f是远平面,所以f<n),它是一个长方体。我们需要做的,就是将正交投影的视锥体转换到标准立方体(即标准化设备坐标,\([-1,1]^{3}\))。注意,这里\([f,n]\)映射到NDC中的[1,-1]。
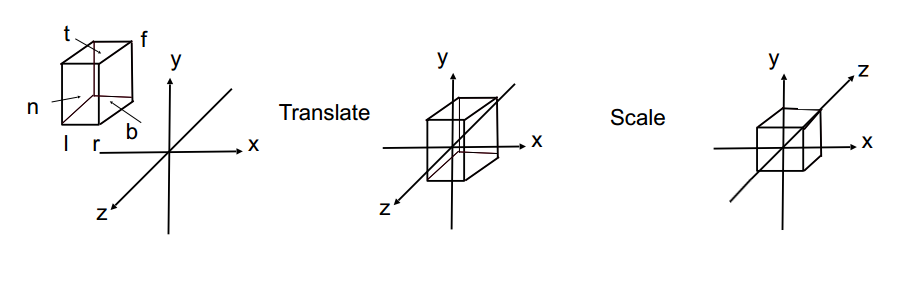
这里,分成两个步骤:平移和缩放。正交投影的矩阵如下:
\[M_{ortho} =
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{f-n} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}=
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\
0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
透视投影
对于透视投影,分成两步操作:
- 首先,“压扁”视锥体成一个长方体(n->n,f->f)(\(M_{persp->ortho}\));
- 然后,做正交投影操作(\(M_{ortho}\),即上面的正交投影)。

观察下图:
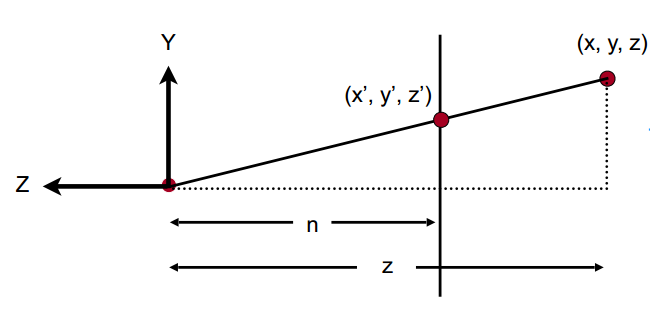
根据相似三角形的关系,可以得出:
\[y^{'} = \frac{n}{z}y
\]
类似的,可以得出:
\[x^{'} = \frac{n}{z}x
\]
由此,可以得出下面的关系:
\[M_{persp->ortho}^{(4 \times 4)}
\begin{pmatrix}
x\\
y\\
z\\
1\\
\end{pmatrix}=
\begin{pmatrix}
\frac{n}{z}x \\
\frac{n}{z}y \\
unknown \\
1 \\
\end{pmatrix}
\]
下面,说一个齐次坐标的性质:在3D坐标系统中,\(\left ( x,y,z,1 \right )\),\(\left ( kx,ky,kz,k \neq 0 \right )\),\(\left ( xz,yz,z^{2},z \neq 0 \right )\)都表示相同的坐标---\(\left ( x,y,z \right )\)。例如:\(\left ( 1,0,0,1 \right )\)和\(\left ( 2,0,0,2 \right )\)都表示坐标\(\left ( 1,0,0 \right )\)。
所以,有如下关系:
\[M_{persp->ortho}^{(4 \times 4)}
\begin{pmatrix}
x\\
y\\
z\\
1\\
\end{pmatrix}=
\begin{pmatrix}
\frac{n}{z}x \\
\frac{n}{z}y \\
unknown \\
1 \\
\end{pmatrix} =
\begin{pmatrix}
nx \\
ny \\
unknown \\
z \\
\end{pmatrix}
\]
更进一步的,可以得到:
\[M_{persp->ortho} =
\begin{pmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0 \\
\end{pmatrix}
\]
现在,还剩下第三列是未知的。
经过观察上面的透视投影视锥体,可以得出以下推论:
-
近平面上的点的坐标都不会改变;
-
远平面上的点,Z坐标不改变。
根据推论1,近平面上的点\(\left (x,y,n,1 \right )\)经过变换后,不会改变。即:
\[M_{persp->ortho}
\begin{pmatrix}
x \\
y \\
n \\
1 \\
\end{pmatrix} =
\begin{pmatrix}
x \\
y \\
n \\
1 \\
\end{pmatrix} =
\begin{pmatrix}
nx \\
ny \\
n^{2} \\
n \\
\end{pmatrix}
\]
根据:
\[M_{persp->ortho}
\begin{pmatrix}
x\\
y\\
z\\
1\\
\end{pmatrix}=
\begin{pmatrix}
nx \\
ny \\
unknown \\
z \\
\end{pmatrix}
\]
因为\(n^{2}\)与x和y都没有关系,所以可以得出\(M_{persp->ortho}\)的第三列的形式是\(\left (0,0,A,B \right )\)。
根据:
\[\left(0,0,A,B \right)
\begin{pmatrix}
x \\
y \\
n \\
1 \\
\end{pmatrix} = n^{2}
\]
可以得出:
\[An+B = n^{2}
\]
根据推论2,远平面的中心点\(\left (0,0,f,1 \right)\),经过变换后,还是本身。如下:
\[M_{persp->ortho}
\begin{pmatrix}
0 \\
0 \\
f \\
1 \\
\end{pmatrix} =
\begin{pmatrix}
0 \\
0 \\
f \\
1 \\
\end{pmatrix} =
\begin{pmatrix}
0 \\
0 \\
f^{2} \\
f \\
\end{pmatrix}
\]
所以,可以得出:
\[\left(0,0,A,B \right)
\begin{pmatrix}
0 \\
0 \\
f \\
1 \\
\end{pmatrix} = f^{2}
\]
即:
\[Af + B = f^{2}
\]
到这里,可以得出方程组:
\[\begin{cases}
An + B = n^{2} \\
Af + B = f^{2} \\
\end{cases} \Rightarrow
\begin{matrix}
A = n + f \\
B = -nf \\
\end{matrix}
\]
到这里,可以得出\(M_{persp->ortho}\):
\[M_{persp->ortho} =
\begin{bmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
\]
最终,透视投影矩阵:
\[M_{persp} =
M_{ortho}M_{persp->ortho} =
\begin{bmatrix}
\frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\
0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0 \\
0 & 0 & \frac{f+n}{f-n} & \frac{2nf}{n-f} \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
\]
裁剪空间->窗口空间
在裁剪空间的最后,所以的可见的点都在标准设备坐标系(NDC)中,即坐标坐落在范围\([-1,1]^{3}\)内。
先不考虑Z轴的变换。
从NDC到窗口空间,需要经过视口变换。定义一个屏幕空间:\(\left (0,0,w,h \right)\)。平面左下角的坐标位\(\left (0,0 \right)\),右上角的坐标为\(\left (w,h \right)\)。对于X和Y坐标的变换,即从\(\left(-1,1\right) \times \left(-1,1\right)\)到\(\left(0,w\right) \times \left(0,h\right)\)。
这里,经过两步变换:
-
将NDC的中心平移到窗口的中心;
\[T_{viewport} =
\begin{pmatrix}
1 & 0 & 0 & \frac{w}{2} \\
0 & 1 & 0 & \frac{h}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\]
-
将NDC的大小缩放到屏幕的大小。
\[R_{viewport} =
\begin{pmatrix}
\frac{w}{2} & 0 & 0 & 0 \\
0 & \frac{h}{2} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\]
合并到一起:
\[M_{viewport} = R_{viewport}T_{viewport} =
\begin{pmatrix}
\frac{w}{2} & 0 & 0 & \frac{w}{2} \\
0 & \frac{h}{2} & 0 & \frac{h}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\]
对于Z坐标,从\(\left(-1,1\right)\)映射到了\(\left(0,1\right)\)。这里只是简单的线性映射。假设\(z^{'} = Az+B\),当\(z\)等于-1时,\(z^{'}\)等于0;当\(z\)等于1时,\(z^{'}\)等于1。可得如下方程组:
\[\begin{cases}
A(-1) + B = 0 \\
A(1) + B = 1 \\
\end{cases} \Rightarrow
\begin{cases}
A = \frac{1}{2} \\
B = \frac{1}{2} \\
\end{cases}
\]
所以,\(z^{'} = \frac{1}{2}z + \frac{1}{2}\)。代入上述\(M_{viewport}\)矩阵,可得:
\[M_{viewport} =
\begin{pmatrix}
\frac{w}{2} & 0 & 0 & \frac{w}{2} \\
0 & \frac{h}{2} & 0 & \frac{h}{2} \\
0 & 0 & \frac{1}{2} & \frac{1}{2} \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\]
参考
-
[1] GAMES101-现代计算机图形学入门-闫令琪
-
[2] OpenGL Projection Matrix
-
[3] Steve Marschner and Peter Shirley,“Fundamentals of Computer Graphics”




