面试官说，你会堆排序吗？会，那好手写一个吧。

## 前言 最近明显文章更新频率降低了，那是因为我在恶补数据结构和算法的相关知识，相当于是从零开始学习。 找了很多视频和资料，最后发现 b 站尚硅谷的视频教程还是相对不错的，总共 195 集。每个小节都是按先概念、原理，然后代码实现的步骤讲解。如果你也准备入门数据结构和算法，我推荐可以看下这个系列教程。  昨天一天一下子肝了 40 多集，从树的后半部分到图的全部部分。可以看到，每一集其实时间也不算长，短的几分钟，长的也就半个小时。开 2 倍速看，倍儿爽。 话不多说，下面进入正题。 ## 二叉堆介绍 我们知道，树有很多种，最常用的就是二叉树了。二叉树又有满二叉树和完全二叉树。而二叉堆，就是基于完全二叉树的一种数据结构。它有以下两个特性。 1. 首先它是一个完全二叉树 2. 其次，堆中的任意一个父节点的值都大于等于（或小于）它的左右孩子节点。 因此，根据第二个特性，就把二叉堆分为大顶堆（或叫最大堆），和小顶堆（或叫最小堆）。 顾名思义，大顶堆，就是父节点大于等于左右孩子节点的堆，小顶堆就是父节点小于左右孩子节点的堆。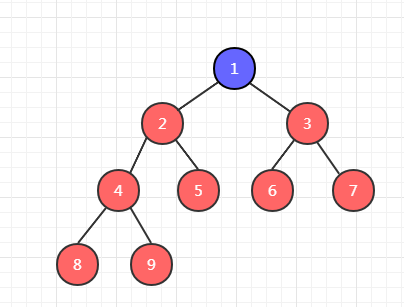 看一下大顶堆的示例图，小顶堆类似，只不过是小值在上而已。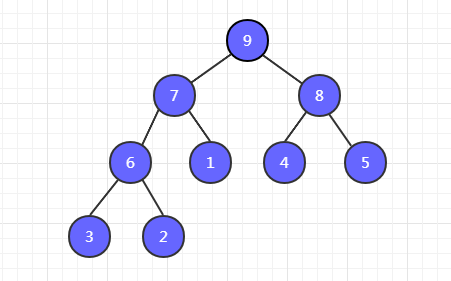  注意：大顶堆只保证父节点大于左右孩子节点的值，不需要保证左右孩子节点之间的大小顺序。如图中，7 的左子节点 6 比右子节点 1 大，而 8 的左子节点 4 却比右子节点 5 小。（小顶堆同理） ## 构建二叉堆 二叉堆的定义我们知道了，那么给你一个无序的完全二叉树，怎么把它构建成二叉堆呢？ 我们以大顶堆为例。给定以下一个数组，（完全二叉树一般用数组来存储） ``` {4, 1, 9, 3, 7, 8, 5, 6, 2} ``` 我们画出它的初始状态，然后分析怎么一步一步构建成大顶堆。  由于大顶堆，父节点的值都大于左右孩子节点，所以树的根节点肯定是所有节点中值最大的。因此，我们需要从树的最后一层开始，逐渐的把大值向上调整（左右孩子节点中较大的节点和父节点交换），直到第一层。 其实，更具体的说，应该是从下面的非叶子节点开始调整。想一想，为什么。 反向思考一下，如果从第一层开始调整的话，例如图中就是 4 和 9 交换位置之后，你不能保证 9 就是所有节点的最大值（额，图中的例子可能不是太好，正好是 9 最大）。如果下边还有比 9 大的数字，你最终还是需要从下面向上遍历调整。那么，我还不如一开始就直接从下向上调整呢。 另外，为什么从从最下面的非叶子节点（图中节点 3 ）开始。因为叶子节点的下面已经没有子节点了，它只能和父节点比较，从叶子节点开始没有意义。 第一步，以 3 为父节点开始，比较他们的子节点 6和 2 ，6最大，然后和 3 交换位置。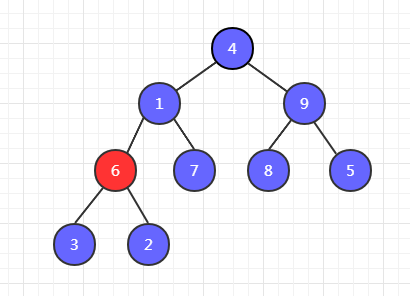  第二步，6 和 7 比较，7 最大，7 和 1 交换位置。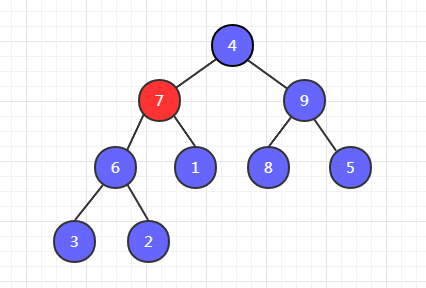  第三步，7 和 9 比较，9 最大，9 和 4 交换位置。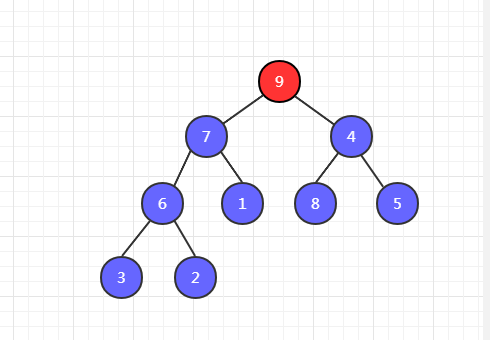  第四步，我们发现交换位置之后，4 下边还有比它大的，因此还需要以 4 为父节点和它的左右子节点进行比较。发现 8 最大，然后 8 和 4 交换位置。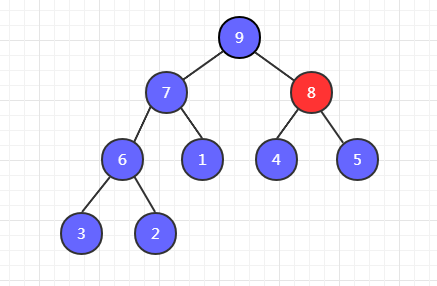  最终，实现了一个大顶堆的构建。下面以代码实现交换过程。 ``` /** * 调整为大顶堆 * @param arr 待调整的数组 * @param parent 当前父节点的下标 * @param length 需要对多少个元素进行调整 */ private static void adjustHeap(int[] arr, int parent, int length){ //临时保存父节点 int temp = arr[parent]; //左子节点的下标 int child = 2 * parent + 1; //如果子节点的下标大于等于当前需要比较的元素个数，则结束循环 while(child < length){ //判断左子节点和右子节点的大小,若右边大，则把child定位到右边 if(child + 1 < length && arr[child] < arr[child + 1]){ child ++; } //若child大于父节点，则交换位置，否则退出循环 if(arr[child] > temp){ //父子节点交换位置 arr[parent] = arr[child]; //因为交换位置之后，不能保证当前的子节点是它子树的最大值，所以需要继续向下比较， //把当前子节点设置为下次循环的父节点，同时，找到它的左子节点，继续下次循环 parent = child; child = 2 * parent + 1; }else{ //如果当前子节点小于等于父节点，则说明此时的父节点已经是最大值了， //因此无需继续循环 break; } } //把当前节点值替换为最开始暂存的父节点值 arr[parent] = temp; } public static void main(String[] args) { int[] arr = {4,1,9,3,7,8,5,6,2}; //构建一个大顶堆，从最下面的非叶子节点开始向上遍历 for (int i = arr.length/2 - 1 ; i >= 0; i--) { adjustHeap(arr,i,arr.length); } System.out.println(Arrays.toString(arr)); } //打印结果： [9, 7, 8, 6, 1, 4, 5, 3, 2]。 和我们分析的结果一模一样 ``` 在 while 循环中，if(arr[child] > temp) else的逻辑， 对应的就是图中的第三步和第四步。即需要确保，交换后的子节点要比它下边的孩子节点都大，不然需要继续循环，调整位置。 ## 堆排序 堆排序就是利用大顶堆或者小顶堆的特性来进行排序的。 它的基本思想就是： 1. 把当前数组构建成一个大顶堆。 2. 此时，根节点肯定是所有节点中最大的值，让它和末尾元素交换位置，则最后一个元素就是最大值。 3. 把剩余的 n - 1个元素重新构建成一个大顶堆，就会得到 n-1 个元素中的最大值。重复执行此动作，就会把所有的元素调整为有序了。 **步骤：** 还是以上边的数组为例，看一下堆排序的过程。 一共有九个元素，把它调整为大顶堆，然后把堆顶元素 9 和末尾元素 2 交换位置。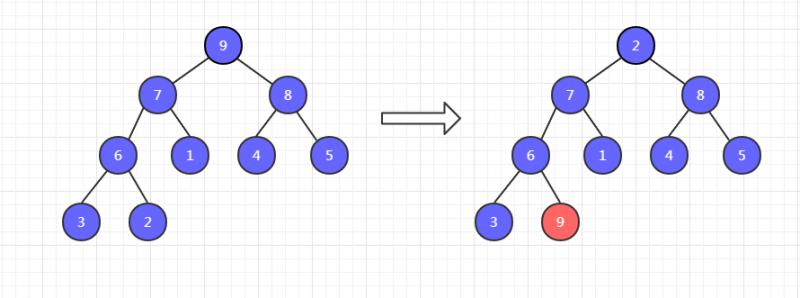  此时，9已经有序了，不需要调整。然后把剩余八个元素调整为大顶堆，再把这八个元素的堆顶元素和末尾元素交换位置，如下，8 和 3 交换位置。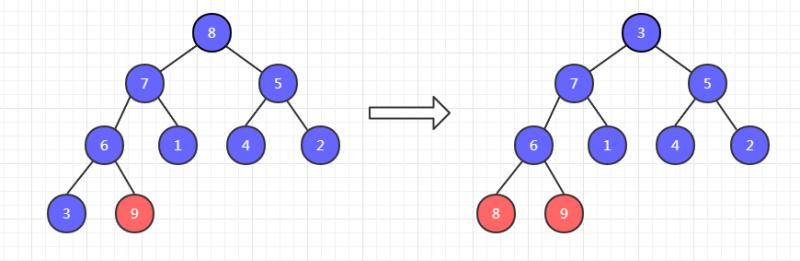  此时，8和 9 已经有序了，不需要调整。然后把剩余七个元素调整为大顶堆，再把这七个元素的堆顶元素和末尾元素交换位置。如下， 7 和 2 交换位置。  以此类推，经过 n - 1 次循环调整，到了最后只剩下一个元素的时候，就不需要再比较了，因为它已经是最小值了。  看起来好像过程很复杂，但其实是非常高效的。没有增删，直接在原来的数组上修改就可以。因为我们知道数组的增删是比较慢的，每次删除，插入元素，都要移动数组后边的 n 个元素。此外，也不占用额外的空间。 代码实现： ``` //堆排序，大顶堆，升序 private static void heapSort(int[] arr){ //构建一个大顶堆，从最下面的非叶子节点开始向上遍历 for (int i = arr.length/2 - 1 ; i >= 0; i--) { adjustHeap(arr,i,arr.length); } System.out.println(Arrays.toString(arr)); //循环执行以下操作：1.交换堆顶元素和末尾元素 2.重新调整为大顶堆 for (int i = arr.length - 1; i > 0; i--) { //将堆顶最大的元素与末尾元素互换，则数组中最后的元素变为最大值 int temp = arr[i]; arr[i] = arr[0]; arr[0] = temp; //从堆顶开始重新调整结构，使之成为大顶堆 // i代表当前数组需要调整的元素个数，是逐渐递减的 adjustHeap(arr,0,i); } } ``` **时间复杂度和空间复杂度：** 堆排序，每次调整为大顶堆的时间复杂度为 O(logn)，而 n 个元素，总共需要循环调整 n-1 次 ，所以堆排序的时间复杂度就是 O(nlogn)。它的数学推导比较复杂，感兴趣的同学可以自己查看相关资料。 由于没有占用额外的内存空间，因此，堆排序的空间复杂度为 O(1)。