机器学习3- 一元线性回归+Python实现

[toc] # 1. 线性模型 给定 $d$ 个属性描述的示例 $\boldsymbol{x} = (x_1; x_2; ...; x_d)$，其中 $x_i$ 为 $\boldsymbol{x}$ 在第 $i$ 个属性上的取值，**线性模型**（*linear model*）试图学得一个通过属性的线性组合来进行预测的函数，即： $$ f(\boldsymbol{x}) = w_1x_1 + w_2x_2 + ... + w_dx_d +b \tag{1.1} $$ 使用向量形式为： $$ f(\boldsymbol{x}) = \boldsymbol{w}^T\boldsymbol{x}+b \tag{1.2} $$ 其中 $\boldsymbol{w} = (w_1;w_2;...;w_d)$，表达了各属性在预测中的重要性。 # 2. 线性回归 给定数据集 $D = \lbrace(\boldsymbol{x}_1,{y}_1), (\boldsymbol{x}_2,{y}_2), ..., (\boldsymbol{x}_m,{y}_m)\rbrace$，其中 $\boldsymbol{x}_i = (x_{i1}; x_{i2}; ...; x_{id})$，$y_i \in \mathbb{R}$。**线性回归**（*linear regression*）试图学得一个能尽可能准确地预测真实输出标记的线性模型，即： $$ f(\boldsymbol{x}_i) = \boldsymbol{w}^T\boldsymbol{x}_i+b \text{，使得} f(\boldsymbol{x}_i) \simeq y_i\tag{1.3} $$ ## 2.1 一元线性回归 先只考虑输入属性只有一个的情况，$D = \lbrace({x}_1,{y}_1), ({x}_2,{y}_2), ..., ({x}_m,{y}_m)\rbrace$，$x_i \in \mathbb{R}$。对离散属性，若属性值存在**序**（*order*）关系，可通过连续化将其转化为连续值。 > 如”高度“属性的取值“高”、“中”、“低”，可转化为$\{1.0, 0.5, 0.0\}$。 若不存在序关系，则假定有 $k$ 种可能的属性值，将其转化为 $k$ 维向量。 > 如“瓜类”属性的取值有“冬瓜”、“西瓜”、“南瓜”，可转化为 $(0,0,1),(0,1,0),(1,0,0)$。 线性回归试图学得： $$ f(x_i) = wx_i+b\text{，使得}f(x_i)\simeq y_i \tag{1.4} $$ 为使 $f(x_i)\simeq y_i$，即：使 $f(x)$ 与 $y$ 之间的差别最小化。 考虑回归问题的常用性能度量——均方误差（亦称平方损失（*square loss*）），即让均方误差最小化： $$ \begin{aligned} (w^*,b^*) = \underset{(w,b)}{arg\ min}\sum_{i=1}^m(f(x_i)-y_i)^2 \\ = \underset{(w,b)}{arg\ min}\sum_{i=1}^m(y_i-wx_i-b)^2 \end{aligned} \tag{1.5} $$ $w^*,b^*$ 表示 $w$ 和 $b$ 的解。 均方误差对应了欧几里得距离，简称欧氏距离（*Euclidean distance*）。 基于均方误差最小化来进行模型求解的方法称为**最小二乘法**（*least square method*）。在线性回归中，就是试图找到一条直线，使得所有样本到直线上的欧氏距离之和最小。 下面需要求解 $w$ 和 $b$ 使得 $E_{(w,b)} = \sum\limits_{i=1}^m(y_i-wx_i-b)^2$ 最小化，该求解过程称为线性回归模型的最小二乘**参数估计**（*parameter estimation*）。 $E_{(w,b)}$ 为关于 $w$ 和 $b$ 的凸函数，当它关于 $w$ 和 $b$ 的导数均为 $0$ 时，得到 $w$ 和 $b$ 的最优解。将 $E_{(w,b)}$ 分别对 $w$ 和 $b$ 求导数得： $$ \frac{\partial{E_{(w,b)}}}{\partial(w)} = 2\Big(w\sum_{i=1}^m x_i^2 - \sum_{i=1}^m (y_i-b)x_i\Big) \tag{1.6} $$ $$ \frac{\partial{E_{(w,b)}}}{\partial(b)} = 2\Big(mb - \sum_{i=1}^m (y_i-wx_i)\Big) \tag{1.7} $$ 令式子 (1.6) 和 (1.7) 为 $0$ 得到 $w$ 和 $b$ 的最优解的闭式（*closed-form*）解： $$ w = \frac{\sum_\limits{i=1}^m y_i(x_i-\overline{x})}{\sum\limits_{i=1}^m x_i^2 - \frac{1}{m}\Big(\sum\limits_{i=1}^m x_i\Big)^2} \tag{1.8} $$ $$ b = \frac{1}{m}\sum_{i=1}^m (y_i-wx_i) \tag{1.9} $$ 其中 $\overline{x} = \frac{1}{m}\sum\limits_{i=1}^m x_i$ 为 $x$ 的均值。 # 3. 一元线性回归的Python实现 现有如下训练数据，我们希望通过分析披萨的直径与价格的线性关系，来预测任一直径的披萨的价格。  其中 `Diameter` 为披萨直径，单位为“英寸”；`Price` 为披萨价格，单位为“美元”。 ## 3.1 使用 stikit-learn ### 3.1.1 导入必要模块 ```python import matplotlib.pyplot as plt import numpy as np import pandas as pd from sklearn.linear_model import LinearRegression ``` ### 3.1.2 使用 Pandas 加载数据 ```python pizza = pd.read_csv("pizza.csv", index_col='Id') pizza.head() # 查看数据集的前5行 ```  ### 3.1.3 快速查看数据 我们可以使用 matplotlib 画出数据的散点图，x 轴表示披萨直径，y 轴表示披萨价格。 ```python def runplt(): plt.figure() plt.title("Pizza price plotted against diameter") plt.xlabel('Diameter') plt.ylabel('Price') plt.grid(True) plt.xlim(0, 25) plt.ylim(0, 25) return plt dia = pizza.loc[:,'Diameter'].values price = pizza.loc[:,'Price'].values print(dia) print(price) plt = runplt() plt.plot(dia, price, 'k.') plt.show() ``` [ 6 8 10 14 18] [ 7. 9. 13. 17.5 18. 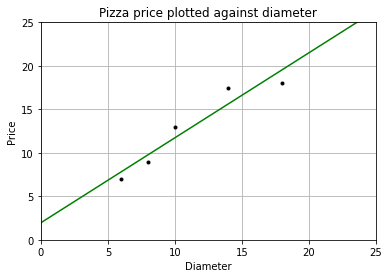]  ### 3.1.4 使用 stlearn 创建模型 ```python model = LinearRegression() # 创建模型 X = dia.reshape((-1,1)) y = price model.fit(X, y) # 拟合 X2 = [[0], [25]] # 取两个预测值 y2 = model.predict(X2) # 进行预测 print(y2) # 查看预测值 plt = runplt() plt.plot(dia, price, 'k.') plt.plot(X2, y2, 'g-') # 画出拟合曲线 plt.show() ``` [ 1.96551724 26.37284483]  这里 `fit()`方法学得了一元线性回归模型 $f(x) = wx+b$，这里 $x$ 指披萨的直径，$f(x)$ 为预测的披萨的价格。 `fit()` 的第一个参数 X 为 shape(样本个数，属性个数) 的数组或矩阵类型的参数，代表输入空间； 第二个参数 y 为 shape(样本个数,) 的数组类型的参数，代表输出空间。 ### 3.1.5 模型评估 成本函数（*cost function*）也叫损失函数（*lost function*），用来定义模型与观测值的误差。 模型预测的价格和训练集数据的差异称为**训练误差**（*training error*）也称**残差**（*residuals*）。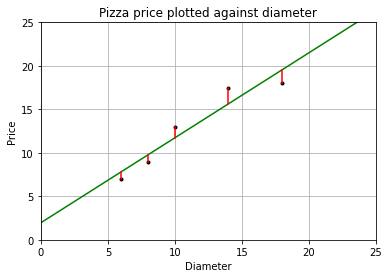 ```python plt = runplt() plt.plot(dia, price, 'k.') plt.plot(X2, y2, 'g-') # 画出残差 yr = model.predict(X) for index, x in enumerate(X): plt.plot([x, x], [y[index], yr[index]], 'r-') plt.show() ```  根据最小二乘法，要得到更高的性能，就是让均方误差最小化，而均方误差就是残差平方和的平均值。 ```python print("均方误差为: %.2f" % np.mean((model.predict(X)-y) ** 2)) ``` 均方误差为: 1.75 ## 3.2 手动实现 ### 3.2.1 计算 w 和 b $w$ 和 $b$ 的最优解的闭式（*closed-form*）解为： $$ w = \frac{\sum_\limits{i=1}^m y_i(x_i-\overline{x})}{\sum\limits_{i=1}^m x_i^2 - \frac{1}{m}\Big(\sum\limits_{i=1}^m x_i\Big)^2} \tag{1.8} $$ $$ b = \frac{1}{m}\sum_{i=1}^m (y_i-wx_i) \tag{1.9} $$ 其中 $\overline{x} = \frac{1}{m}\sum\limits_{i=1}^m x_i$ 为 $x$ 的均值。 下面使用 Python 计算 $w$ 和 $b$ 的值： ```python w = np.sum(price * (dia - np.mean(dia))) / (np.sum(dia**2) - (1https://img.qb5200.com/download-x/dia.size) * (np.sum(dia))**2) b = (1 / dia.size) * np.sum(price - w * dia) print("w = %f\nb = %f" % (w, b)) y_pred = w * dia + b plt = runplt() plt.plot(dia, price, 'k.') # 样本点 plt.plot(dia, y_pred, 'b-') # 手动求出的线性回归模型 plt.plot(X2, y2, 'g-.') # 使用LinearRegression.fit()求出的模型 plt.show() ``` w = 0.976293 b = 1.965517  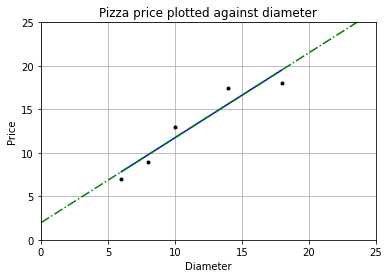可以看到两条直线重合，我们求出的回归模型与使用库求出的回归模型相同。 ### 3.2.2 功能封装 将上述代码封装成类： ```python class LinearRegression: """ 拟合一元线性回归模型 Parameters ---------- x : shape 为(样本个数,)的 numpy.array 只有一个属性的数据集 y : shape 为(样本个数,)的 numpy.array 标记空间 Returns ------- self : 返回 self 的实例. """ def __init__(self): self.w = None self.b = None def fit(self, x, y): self.w = np.sum(y * (x - np.mean(x))) / (np.sum(x**2) - (1/x.size) * (np.sum(x))**2) self.b = (1 / x.size) * np.sum(y - self.w * x) return self def predict(self, x): """ 使用该线性模型进行预测 Parameters ---------- x : 数值 或 shape 为(样本个数,)的 numpy.array 属性值 Returns ------- C : 返回预测值 """ return self.w * x + self.b ``` 使用： ```python # 创建并拟合模型 model = LinearRegression() model.fit(dia, price) x2 = np.array([0, 25]) # 取两个预测值 y2 = model.predict(x2) # 进行预测 print(y2) # 查看预测值 runplt() plt.plot(dia, price, 'b.') plt.plot(x2, y2, 'y-') # 画出拟合 plt.show() ``` [ 1.96551724 26.37284483]  ----------- 此文原创禁止转载，转载文章请联系博主并注明来源和出处，谢谢！ 作者: Raina_RLN https://www.cnblogs.com/raina/